高阶调制中的比特可靠性

看书时，看到了这么一句话：

由于在高阶QAM调制符号中，各比特的可靠性是不同的，例如一个256QAM调制符号对应了8个比特，其中，最前面的两个比特可靠性最高；第3和第4比特的可靠性次之；第5和第6比特可靠性再差一些；最后面的两个比特可靠性最差。

这是为什么呢？

x=[0:255];
y=qammod(x,256,'gray');
xbin=dec2bin(x,8);
figure;
for bitIdx=1:8
    subplot(2,4,bitIdx);
    [r]=find(xbin(:,bitIdx)=='0');scatter(real(y(r)),imag(y(r)));hold on;
    [r]=find(xbin(:,bitIdx)=='1');scatter(real(y(r)),imag(y(r)));hold off;
    str = sprintf('第 %d 比特',bitIdx);
    legend('0','1');title(str);axis([-15 25 -15 15]);
end

运行图示程序，得到如下结果：

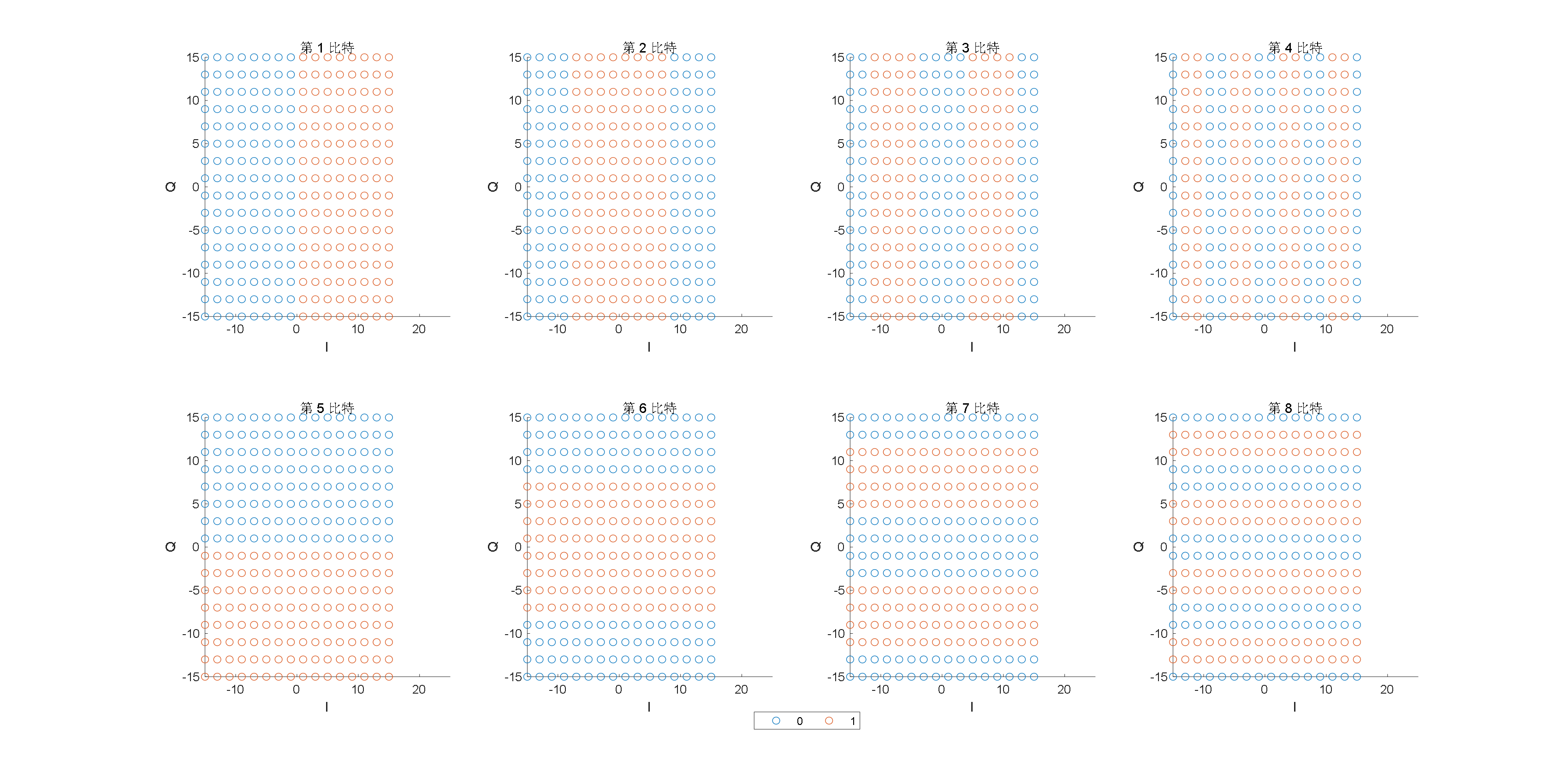
事实上，前4个比特映射到了I路，后四个比特则映射到了Q路。在解调时，IQ可以分别进行解调，不失一般性，我们分析一下第1~4比特。
从直观上看，第1个比特的分布最为集中，也最不容易发生误判；
第二个比特次集中，略微容易发生误判；
第三个比特则更为分散，更易发生误判；
第四个比特则非常分散，很容易发生误判。
实际上，我们也可以度量四个比特的LLR的平均值，得到其平均可靠性度量。[1]
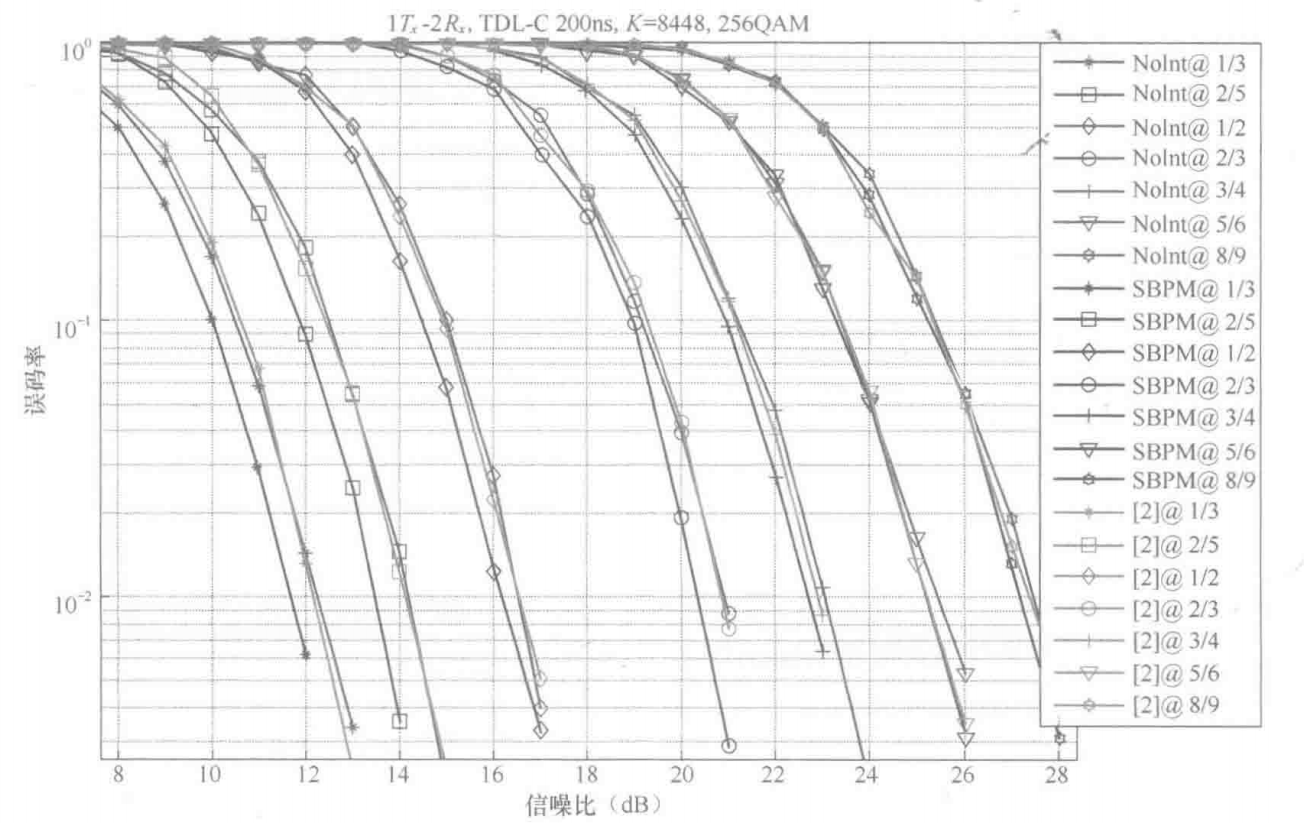
这大概就是文中所述的高阶调制星座点不同位置的比特具有不同的可靠性，而通过合适地交织和调整比特顺序，将信息位放在高可靠的比特位置，可以提升译码性能。相较于不使用交织，在调制前进行比特级交织，交织宽度为调制阶数时，在高阶调制时能获得约0.5dB的增益。

参考文献：
[1]顾昕钰,王艺晨,于笑博,等.基于64-QAM的星座图重排高级混合ARQ技术[J].电子与信息学报,2005,(11):8-12.