深度学习面试题
1. 什么是深度学习?与机器学习的区别是什么?
深度学习(Deep Learning) 是一种特殊的机器学习方法,使用由多层非线性变换组成的神经网络来进行特征提取和学习,尤其擅长处理图像、语音、文本等非结构化数据。
| 对比维度 | 机器学习 | 深度学习 |
|---|---|---|
| 特征提取 | 需要人工设计 | 自动从数据中学习抽象特征 |
| 模型结构 | 较浅(如 SVM, 决策树等) | 通常为多层神经网络(深) |
| 数据依赖 | 对小数据集适应性较好 | 依赖大量数据才能发挥优势 |
| 性能表现 | 精度有限,特定任务可能足够 | 在图像识别、自然语言等任务上领先 |
2. 什么是感知机?它有哪些局限性?
感知机(Perceptron) 是最早的神经网络模型之一,由 Frank Rosenblatt 在 1958 年提出。它是一个线性二分类器,基本结构包括输入层、权重、偏置和一个激活函数。
公式表示:
其中 \(f\) 通常是阶跃函数(step function)。
单位阶跃函数(Unit Step Function),是一种非连续激活函数
它的定义是:
其中 $z = \sum_{i=1}^{n} w_i x_i + b$ 是输入的加权和。
局限性:
- 只能处理线性可分问题:如异或(XOR)问题无法被单层感知机正确分类。
- 无隐藏层结构:表达能力有限,不能进行复杂特征抽象。
- 训练收敛性差:对于线性不可分的数据集无法收敛。
多层感知机(MLP)和激活函数的引入才使得感知机进化为更强大的神经网络模型。
3. 神经网络为什么可以拟合非线性函数?
原因主要在于以下几点:
-
非线性激活函数:如 ReLU、sigmoid、tanh 等可以引入非线性变换,使模型能逼近复杂函数。
-
多层结构(深度):每一层通过线性变换+非线性激活进行组合,层层堆叠后,具备了“通用逼近能力”。
-
通用逼近定理(Universal Approximation Theorem):
单隐层的前馈神经网络在给定足够的神经元时可以逼近任意连续函数。
因此,深度神经网络具有强大的拟合能力,不仅能处理线性问题,还能学习图像、语音、文本等复杂结构数据中的高阶特征。
4. 激活函数的作用是什么?常见激活函数有哪些?
作用:
- 引入非线性能力,使网络能拟合复杂函数。
- 控制信息流动,增加网络表达能力。
- 影响梯度传播效率与收敛速度。
好的,以下是包含图片列的新表格版本,整合了你已经添加的可视化图像链接:
常见激活函数:
| 激活函数 | 定义 | 特点 | 图片 |
|---|---|---|---|
| Sigmoid | $\sigma(x) = \frac{1}{1 + e^{-x}}$ | 饱和梯度问题,输出在 (0,1) | 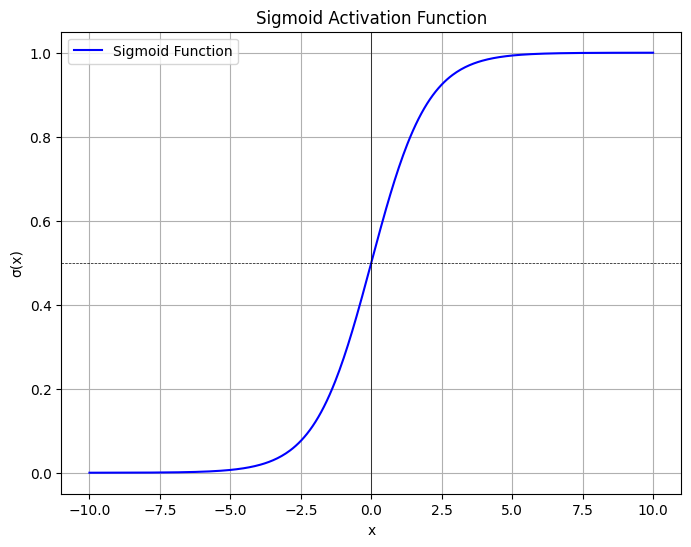 |
| Tanh | $\tanh(x) = \frac{e^x - e{-x}}{ex + e^{-x}}$ | 输出在 (-1,1),对称,但仍有梯度消失问题 | 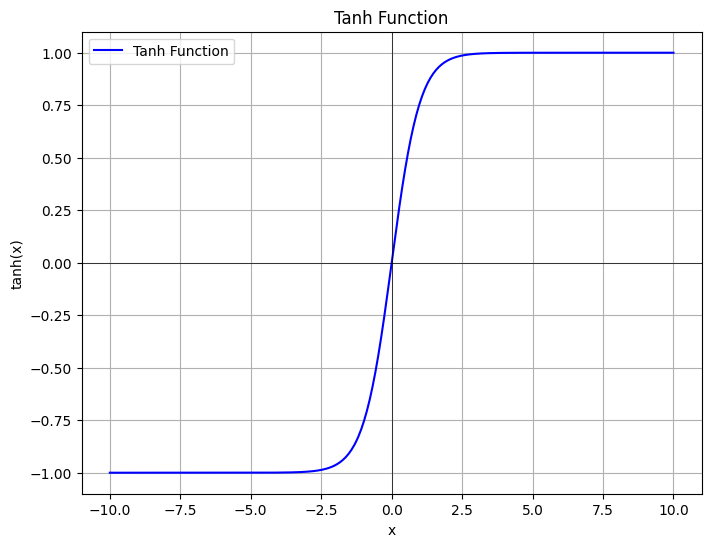 |
| ReLU | $\text{ReLU}(x) = \max(0, x)$ | 简单高效,避免梯度消失,但可能神经元死亡 | 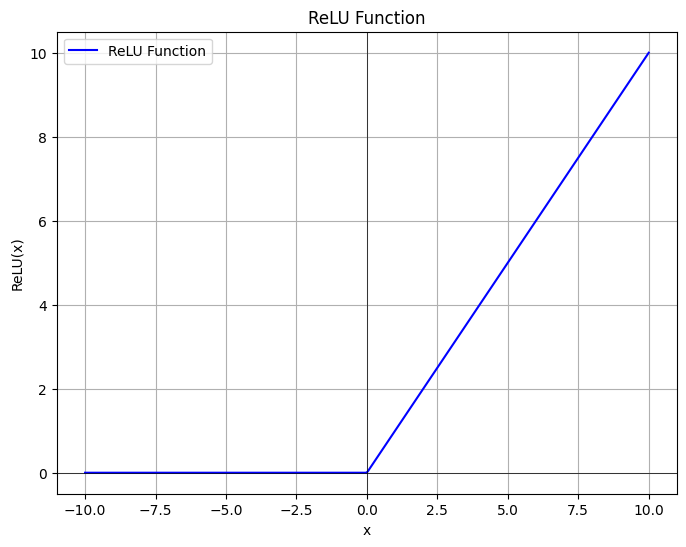 |
| Leaky ReLU | $\text{LeakyReLU}(x) = \max(\alpha x, x)$,$\alpha\in(0,1)$ | 缓解神经元死亡问题,允许负梯度传递 | 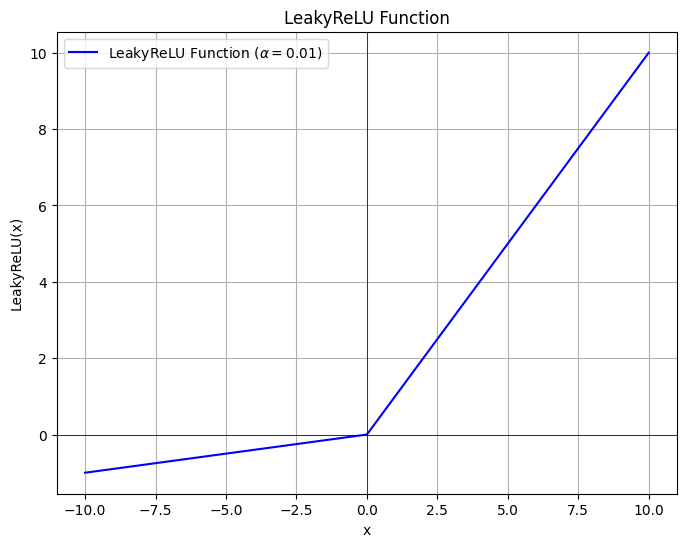 |
| GELU | 高斯误差线性单元,常用于 BERT/GPT 等大模型 | 表现更优但计算复杂,近似为 $0.5x(1 + \tanh(...))$ | 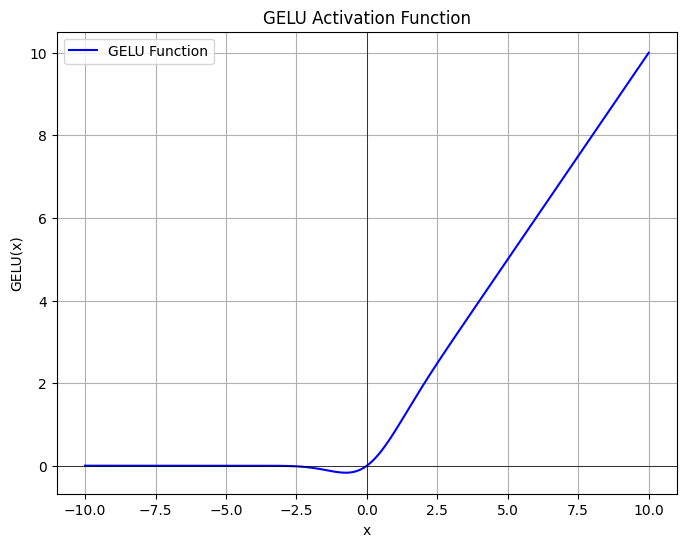 |
5. 为什么使用 ReLU 激活函数比 Sigmoid 更常见?
ReLU(Rectified Linear Unit)优于 Sigmoid 的原因主要有:
- 避免梯度消失问题:Sigmoid 在输入较大/较小时梯度趋近于零,影响深层网络训练;ReLU 在 \(x>0\) 时梯度恒为 1。
- 计算效率高:ReLU 只涉及最大值判断,不需要指数计算。
- 稀疏激活(Sparsity):ReLU 会使部分神经元输出为 0,增加模型稀疏性,提高泛化能力。
- 更快收敛:实际训练中使用 ReLU 通常可以加速梯度下降过程。
6. 什么是前向传播和反向传播?
前向传播(Forward Propagation)
- 将输入数据经过每层网络的线性变换与激活函数依次计算出最终输出。
- 计算每一层的输出 \(a = f(Wx + b)\)。
- 最终输出经过损失函数计算得到 loss 值。
反向传播(Backward Propagation)
- 用链式法则(Chain Rule)从损失函数反向计算每层的梯度。
- 更新权重参数:使用梯度下降(或其变体)调整 \(W, b\),以最小化损失函数。
- 每一层的误差是下一层误差通过权重矩阵反向传播回来的。
关键要素:
- 计算损失函数相对于每个参数的偏导数。
- 使用优化算法(如 SGD, Adam)进行参数更新。
你列的这些都是神经网络基础且重要的问题,下面我帮你整理一份简明且清晰的回答:
7. 神经网络中的梯度下降原理是什么?
梯度下降(Gradient Descent)是一种优化算法,用于通过不断调整模型参数(权重和偏置)以最小化损失函数。
原理:
- 计算损失函数相对于参数的梯度(偏导数)。
- 参数沿梯度负方向更新(即减少损失):
\(\theta \leftarrow \theta - \eta \nabla_\theta L(\theta)\)
其中,$\theta$ 是参数,$\eta$ 是学习率,$L$ 是损失函数。 - 通过多次迭代,参数逐步逼近最优值。
8. 为什么神经网络中容易出现梯度消失/爆炸问题?
- 梯度消失: 反向传播时,链式法则中多层的梯度乘积导致梯度越来越小,特别是在 Sigmoid 或 Tanh 激活函数时,梯度被压缩到接近0,导致前层参数几乎不更新,网络难以训练深层特征。
- 梯度爆炸: 相反,梯度乘积可能会变得非常大,导致参数更新步伐过大,使训练不稳定甚至发散。
原因主要是网络深度太大、权重初始化不合理、激活函数选择等。
9. 什么是损失函数?有哪些常见的损失函数?
-
**损失函数(Loss Function)**用于衡量模型预测输出与真实标签之间的差异,是训练神经网络的优化目标。
-
常见损失函数:
- 均方误差(MSE):回归问题
- 交叉熵(Cross-Entropy):分类问题
- Hinge Loss:支持向量机等
- KL 散度:概率分布差异度量
- 自定义损失:根据任务设计
10. L1 与 L2 正则化的区别是什么?
| 正则化类型 | 定义 | 作用 | 影响 | ||
|---|---|---|---|---|---|
| L1 正则化 | 参数绝对值和:$ \lambda \sum | w_i | $ | 促使权重稀疏化,产生稀疏模型(很多权重为零) | 有助于特征选择,模型更简洁 | ||
| L2 正则化 | 参数平方和:$ \lambda \sum w_i^2 $ | 防止权重过大,平滑模型 | 权重较小且均匀分布,减少过拟合 |
11. 什么是 epoch、batch、iteration?
- Epoch(轮次):完整遍历一次训练数据集。
- Batch(批次):一次训练中使用的数据子集,样本数量称为 batch size。
- Iteration(迭代次数):模型参数更新的次数。
关系:
\(\text{iterations per epoch} = \frac{\text{训练集样本总数}}{\text{batch size}}\)
12. 什么是学习率?如何选择合适的学习率?
-
**学习率(Learning Rate)**是梯度下降时控制参数更新步长的超参数。
-
选择原则:
- 学习率过大,训练不稳定,甚至发散。
- 学习率过小,训练收敛缓慢,可能陷入局部最优。
-
常用方法:
- 使用经验值(如 0.001、0.01 等)开始调试。
- 学习率调度器(逐渐减小学习率)。
- 自适应优化算法(Adam、RMSProp)自动调整。
- 观察训练曲线,调整学习率。
以下是第 13~18 题的简洁清晰答案,适用于笔记、复习或面试:
13. 什么是参数、超参数?举例说明。
-
参数(Parameters):
模型在训练中自动学习得到的值,比如神经网络的权重和偏置。
例: 全连接层中的权重矩阵、LSTM 中的门控权重。 -
超参数(Hyperparameters):
在训练前人工设定的参数,不能通过训练数据学习。
例: 学习率、batch size、epoch 数、网络层数、激活函数、Dropout 比例等。
14. 什么是权重初始化?有哪些常见方法?
-
定义:
在神经网络训练开始前,需要为每一层的权重赋初始值,这个过程称为权重初始化。初始化方式会直接影响收敛速度和训练效果。 -
常见方法:
方法 描述 适用场景 零初始化 所有权重为 0(不可取) 会导致所有神经元学习到相同特征,无法破坏对称性 随机初始化 使用正态或均匀分布随机初始化 简单,但容易导致梯度爆炸/消失 Xavier 初始化 方差与输入输出节点数相关,均衡传播 适合 sigmoid / tanh He 初始化 方差考虑了 ReLU 的非对称性 适合 ReLU / LeakyReLU
15. 什么是 Dropout?它的作用是什么?
-
定义:
Dropout 是一种正则化技术,训练时随机“丢弃”部分神经元(将其输出设为0),防止模型过拟合。 -
作用:
- 增强模型鲁棒性,避免对某些神经元过度依赖。
- 相当于对不同子网络的平均,有集成效果。
- 提高泛化能力。
16. 神经网络中的 Batch Normalization 有什么作用?
-
定义:
BatchNorm 是对每一层输入进行标准化(均值为 0,方差为 1),常用于加速训练和提升性能。 -
作用:
- 减少内部协变量偏移(internal covariate shift)
- 允许使用更高学习率,加快收敛
- 缓解梯度消失/爆炸
- 具有轻微正则化效果,降低过拟合
17. 什么是 Early Stopping?
-
定义:
Early Stopping 是一种防止过拟合的策略:在验证集性能不再提升时提前停止训练。 -
作用:
- 避免模型在训练集上过度拟合
- 节省训练时间和资源
- 常配合验证集和 patience(耐心轮数)使用
18. 什么是 Overfitting 和 Underfitting?
| 状态 | 描述 | 特征 | 解决方案 |
|---|---|---|---|
| 过拟合(Overfitting) | 模型对训练集拟合太好,但泛化能力差 | 训练误差低,验证/测试误差高 | 加正则化、增加数据、简化模型、使用 Dropout |
| 欠拟合(Underfitting) | 模型过于简单,无法捕捉数据的潜在规律 | 训练误差和验证误差都很高 | 增加模型复杂度、训练更久、特征工程优化 |
以下是第 19~24 题的专业整理,适合面试复习或讲义笔记使用:
19. 为什么深层网络更容易过拟合?
-
原因:
- 参数更多: 深层网络拥有更多的权重与自由度,容易精确拟合训练数据的噪声。
- 容量更强: 模型复杂度越高,学习能力越强,也越容易学习到训练集中的偶然性特征。
- 训练集不足或数据质量不高时,过拟合更明显。
-
解决方法:
- 使用正则化(L1/L2、Dropout、BN)
- 提高数据质量或增强数据量(Data Augmentation)
- 使用 Early Stopping 等策略
20. 什么是数据标准化与归一化?
| 类型 | 定义 | 公式 | 适用场景 |
|---|---|---|---|
| 标准化(Standardization) | 将数据转换为均值为 0,标准差为 1 的分布 | $z = \frac{x - \mu}{\sigma}$ | 假设数据服从正态分布时 |
| 归一化(Normalization) | 将数据缩放到固定区间(如 [0,1]) | $x' = \frac{x - \min}{\max - \min}$ | 不要求数据分布时,如图像灰度值处理 |
- 目的: 让各特征维度具有相同量级,便于模型收敛,加快训练速度,提高稳定性。
21. 多层感知机(MLP)结构是怎样的?
-
结构:
-
一种前馈神经网络,由输入层 → 多个隐藏层 → 输出层组成。
-
每一层是一个线性变换(权重乘法)加一个激活函数:
\[a^{(l)} = f(W^{(l)} a^{(l-1)} + b^{(l)}) \]
-
-
特点:
- 层与层之间全连接(Fully Connected)
- 可以逼近任意连续函数(通用近似器)
- 不具备局部感知与参数共享(适用于结构化数据)
22. 卷积神经网络(CNN)原理是什么?
-
CNN 是专为图像等结构化数据设计的神经网络,核心思想是:
- 局部连接: 每个神经元只连接输入的一小块区域,提取局部特征。
- 参数共享: 使用同一个卷积核在不同位置滑动,减少参数数量。
- 特征层叠加深: 从低级边缘/纹理到高级语义(如物体)逐层提取特征。
-
典型结构:
Conv → ReLU → Pooling → Conv → … → Flatten → FC → Softmax
23. 什么是卷积核?可学习吗?
-
定义:
卷积核(或滤波器)是一个小的权重矩阵,滑动于输入特征图上,执行加权求和(卷积操作),输出新的特征图(Feature Map)。 -
是可学习的参数,和全连接层的权重一样,通过反向传播自动更新。
-
作用:
- 提取边缘、角点、纹理等特征
- 随着训练深入,能学习更复杂的模式(如眼睛、物体等)
24. 什么是 Padding?为什么需要 Padding?
-
定义:
Padding 是指在输入边缘补零(或其他值),使卷积操作不会因边缘而丢失信息。 -
作用:
- 保持特征图尺寸不变(常见为“same padding”)
- 防止边缘信息丢失,提高模型对图像边缘区域的感知能力
- 控制输出尺寸,便于网络结构设计(特别是深层网络)
-
常用方式:
- Valid Padding(无填充):输出尺寸变小
- Same Padding(适当填充):输出尺寸与输入相同
这里是第25~30题的详细解析,帮你理解卷积神经网络关键概念和优化思路:
25. 什么是 Stride?对特征图的影响是什么?
-
Stride(步长) 指卷积核在输入特征图上滑动时的步幅大小。
-
影响:
- 步长越大,输出特征图尺寸越小(采样更稀疏),减少计算量。
- 步长为1时,卷积核逐像素滑动,输出尺寸最大。
-
公式(假设无填充):
\[\text{Output Size} = \frac{\text{Input Size} - \text{Kernel Size}}{\text{Stride}} + 1 \]
26. 池化操作(Pooling)有哪些类型?作用是什么?
-
类型:
- 最大池化(Max Pooling): 取池化窗口内最大值。
- 平均池化(Average Pooling): 取池化窗口内平均值。
- 全局池化(Global Pooling): 对整个特征图做池化,输出一个数。
-
作用:
- 降低特征图尺寸,减少计算量和参数数量。
- 提取重要特征,增强平移不变性。
- 防止过拟合。
27. CNN 如何提取图像特征?
- 通过局部感受野和权重共享机制,卷积层滑动卷积核提取局部低级特征(边缘、纹理)。
- 多层卷积叠加后,网络逐渐抽象为更高级的语义特征(物体形状、部件)。
- 通过激活函数引入非线性,捕获复杂模式。
- 池化层降低空间维度,同时保留关键特征。
28. 什么是转置卷积(Deconv)?用途是什么?
-
定义: 转置卷积是一种逆向卷积操作,用于将低分辨率特征图**放大(上采样)**为高分辨率特征图。
-
用途:
- 图像生成(GANs)
- 语义分割中的上采样
- 超分辨率重建等任务
29. 卷积层与全连接层的参数量对比?
| 层类型 | 参数计算 | 说明 |
|---|---|---|
| 全连接层 | 输入维度 × 输出维度 + 偏置数量 | 参数量大,容易过拟合 |
| 卷积层 | 卷积核大小 × 输入通道数 × 输出通道数 + 偏置数 | 参数共享,参数量远小于全连接层 |
- 卷积层参数与输入大小无关,主要与卷积核大小和通道数相关。
30. 卷积神经网络中如何减少计算量?
-
方法:
- 使用较小卷积核(如3×3代替5×5)
- 使用步长(Stride)大于1进行下采样
- 利用池化层降低空间尺寸
- 使用深度可分离卷积(Depthwise Separable Convolution)
- 采用瓶颈结构(如ResNet中的1×1卷积减少通道数)
- 网络剪枝和量化等模型压缩技术
31. 什么是 ResNet?残差连接的原理是什么
ResNet 是一类引入「残差结构(Residual Block)」的深层网络结构,常见的版本有 ResNet-18、ResNet-34、ResNet-50、ResNet-101 等,它们分别表示网络中使用的层数。
ResNet 的核心思想是:与其直接学习一个映射 H(x),不如让网络学习一个残差函数:
其中:
- H(x):期望学习的映射
- F(x):实际由网络学习的残差
- x:输入,直接跳跃到输出层
这样网络只需要学习“相对于输入的差异”,学习目标更简单,优化更容易。
残差块结构如下:
x
│
┌───▼────┐
│ │
│ F(x) │ ← 两个或多个 conv → BN → ReLU 层
│ │
└───▲────┘
│
+ ← 残差加法:F(x) + x
│
ReLU
即:
如果 F(x) → 0,那么整个模块就变成了 identity:输出就是输入 x,不影响信息流。
这在深层网络中非常重要,能有效避免梯度消失或爆炸。
ResNet 作用
-
减少退化问题:
传统深度网络很难训练太深,ResNet 让 100+ 层的网络也能收敛。 -
梯度更容易传播:
残差连接允许梯度直接传到浅层,缓解梯度消失问题。 -
简单灵活:
残差模块很容易堆叠、复用、拓展,适用于各种任务。
下面是一个最简单的残差块实现:
import torch.nn as nn
import torch.nn.functional as F
class ResidualBlock(nn.Module):
def __init__(self, channels):
super().__init__()
self.conv1 = nn.Conv2d(channels, channels, 3, padding=1)
self.bn1 = nn.BatchNorm2d(channels)
self.conv2 = nn.Conv2d(channels, channels, 3, padding=1)
self.bn2 = nn.BatchNorm2d(channels)
def forward(self, x):
identity = x
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += identity # 残差连接
return F.relu(out)
当然可以,下面是 GRU(Gated Recurrent Unit)的简明逻辑解释:
GRU?
GRU(门控循环单元)是 RNN 的一种改进结构,由 Cho 等人于 2014 年提出,目的是缓解标准 RNN 在训练中遇到的长期依赖问题,比如梯度消失。
GRU 和 LSTM 类似,但结构更简单,参数更少,计算更快。
GRU 的核心思想
GRU 使用了两个「门」来控制信息的流动:
| 门类型 | 作用 |
|---|---|
| 更新门 zₜ | 决定保留多少旧的信息 hₜ₋₁ |
| 重置门 rₜ | 决定丢弃多少旧的信息 hₜ₋₁(用于计算候选状态) |
数学公式
给定输入 xₜ 和上一状态 hₜ₋₁,GRU 的计算步骤如下:
-
计算更新门 zₜ:
zₜ = σ(W_z xₜ + U_z hₜ₋₁) -
计算重置门 rₜ:
rₜ = σ(W_r xₜ + U_r hₜ₋₁) -
计算候选隐藏状态 h̃ₜ:
h̃ₜ = tanh(W_h xₜ + U_h (rₜ ⊙ hₜ₋₁)) -
最终隐藏状态 hₜ:
hₜ = (1 - zₜ) ⊙ hₜ₋₁ + zₜ ⊙ h̃ₜ
其中:
- σ 是 Sigmoid 函数
- tanh 是双曲正切函数
- ⊙ 表示按元素相乘(Hadamard积)
为什么 GRU 有用?
- 它可以自动决定要保留什么、遗忘什么,无需人工设置。
- 比 RNN 更容易训练、效果更好。
- 通常在小数据集或计算资源有限时,GRU 是比 LSTM 更好的选择。
代码
class SimpleGRUCell(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# 更新门 z,重置门 r,候选状态 h~
self.Wz = nn.Parameter(torch.randn(input_size, hidden_size))
self.Uz = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.Wr = nn.Parameter(torch.randn(input_size, hidden_size))
self.Ur = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.Wh = nn.Parameter(torch.randn(input_size, hidden_size))
self.Uh = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.bz = nn.Parameter(torch.zeros(hidden_size))
self.br = nn.Parameter(torch.zeros(hidden_size))
self.bh = nn.Parameter(torch.zeros(hidden_size))
def forward(self, x_t, h_prev):
z_t = torch.sigmoid(x_t @ self.Wz + h_prev @ self.Uz + self.bz)
r_t = torch.sigmoid(x_t @ self.Wr + h_prev @ self.Ur + self.br)
h_hat = torch.tanh(x_t @ self.Wh + (r_t * h_prev) @ self.Uh + self.bh)
h_t = (1 - z_t) * h_prev + z_t * h_hat
return h_t
class SimpleGRU(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.hidden_size = hidden_size
self.gru_cell = SimpleGRUCell(input_size, hidden_size)
def forward(self, x):
batch_size, seq_len, _ = x.size()
h = torch.zeros(batch_size, self.hidden_size, device=x.device)
outputs = []
for t in range(seq_len):
x_t = x[:, t, :]
h = self.gru_cell(x_t, h)
outputs.append(h.unsqueeze(1))
return torch.cat(outputs, dim=1)
RNN
RNN 公式
\( hₜ = tanh(Wₓ·xₜ + Wₕ·hₜ₋₁ + b) \)
RNN 为什使用 tanh 作为激活函数
- :tanh 的输出范围为 [-1, 1]
- 可以很好地“压缩”信息,避免过大的值在时序传播中爆炸。
- 与 sigmoid(0~1)相比,tanh 的零均值(中心对称)更利于梯度传播。
- :tanh 是平滑、可微的非线性函数
- RNN 需要在时间序列上传播梯度,tanh 的连续导数在反向传播中表现良好。
- :历史原因和经验积累
- 早期的 RNN 网络(如 Elman 网络)使用 tanh 的经验较多,标准实现如 PyTorch 的 nn.RNN 也默认使用 tanh。
可选:
- 有些变种也会使用 ReLU 作为激活函数,但由于 RNN 有递归结构,ReLU 更容易导致梯度爆炸或“死神经元”,所以不如 tanh 稳定。
- LSTM、GRU 内部也大量使用 sigmoid 和 tanh 组合调控门控结构。
RNN 实现
# RNN实现(仅用矩阵运算)
class SimpleRNNCell(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.Wx = nn.Parameter(torch.randn(input_size, hidden_size))
self.Wh = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.b = nn.Parameter(torch.zeros(hidden_size))
def forward(self, x_t, h_prev):
h_t = torch.tanh(x_t @ self.Wx + h_prev @ self.Wh + self.b)
return h_t
class SimpleRNN(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.hidden_size = hidden_size
self.rnn_cell = SimpleRNNCell(input_size, hidden_size)
def forward(self, x):
batch_size, seq_len, _ = x.size()
h = torch.zeros(batch_size, self.hidden_size, device=x.device)
outputs = []
for t in range(seq_len):
x_t = x[:, t, :]
h = self.rnn_cell(x_t, h)
outputs.append(h.unsqueeze(1))
return torch.cat(outputs, dim=1)
LSTM
LSTM 关键公式:
在时间步 \(t\),LSTM 单元接收输入 \(x\_t\) 和前一个时间步的隐藏状态 \(h\_{t-1}\) 以及细胞状态 \(c\_{t-1}\),并计算当前的隐藏状态 \(h\_t\) 和细胞状态 \(c\_t\)。
-
遗忘门 (Forget Gate):
\[f_t = \sigma(W_{xf} x_t + W_{hf} h_{t-1} + b_f) \] -
输入门 (Input Gate):
- 更新门:\[i_t = \sigma(W_{xi} x_t + W_{hi} h_{t-1} + b_i) \]
- 候选细胞状态:\[\tilde{c}_t = \tanh(W_{xc} x_t + W_{hc} h_{t-1} + b_c) \]
- 更新门:
-
输出门 (Output Gate):
\[o_t = \sigma(W_{xo} x_t + W_{ho} h_{t-1} + b_o) \] -
细胞状态更新:
\[c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t \] -
隐藏状态:
\[h_t = o_t \odot \tanh(c_t) \] -
输出 (通常基于 \(h\_t\)):
\[y_t = W_{hy} h_t + b_y \]
import torch
from torch import nn
class SimpleMatrixLSTM(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim, device=None):
super(SimpleMatrixLSTM, self).__init__()
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
self.device = device if device is not None else torch.device('cpu')
def normal(shape):
return torch.randn(size=shape, device=self.device) * 0.01
# Input gate
self.W_xi = nn.Parameter(normal((input_dim, hidden_dim)))
self.W_hi = nn.Parameter(normal((hidden_dim, hidden_dim)))
self.b_i = nn.Parameter(torch.zeros(hidden_dim, device=self.device))
# Forget gate
self.W_xf = nn.Parameter(normal((input_dim, hidden_dim)))
self.W_hf = nn.Parameter(normal((hidden_dim, hidden_dim)))
self.b_f = nn.Parameter(torch.zeros(hidden_dim, device=self.device))
# Cell gate
self.W_xc = nn.Parameter(normal((input_dim, hidden_dim)))
self.W_hc = nn.Parameter(normal((hidden_dim, hidden_dim)))
self.b_c = nn.Parameter(torch.zeros(hidden_dim, device=self.device))
# Output gate
self.W_xo = nn.Parameter(normal((input_dim, hidden_dim)))
self.W_ho = nn.Parameter(normal((hidden_dim, hidden_dim)))
self.b_o = nn.Parameter(torch.zeros(hidden_dim, device=self.device))
# Output layer
self.W_hy = nn.Parameter(normal((hidden_dim, output_dim)))
self.b_y = nn.Parameter(torch.zeros(output_dim, device=self.device))
def forward(self, inputs, state):
"""
前向传播 LSTM。
Args:
inputs (torch.Tensor): 输入序列,形状为 (batch_size, seq_len, input_dim)。
state (tuple): 包含初始隐藏状态 (h_0) 和细胞状态 (c_0),
每个形状为 (batch_size, hidden_dim)。
Returns:
tuple:
- outputs (torch.Tensor): 所有时间步的输出,形状为 (batch_size, seq_len, output_dim)。
- (h_n, c_n) (tuple of torch.Tensor): 最终的隐藏状态和细胞状态。
"""
seq_len = inputs.shape[1]
batch_size = inputs.shape[0]
outputs = []
h, c = state
for t in range(seq_len):
x_t = inputs[:, t, :] # (batch_size, input_dim)
# Input gate
i_t = torch.sigmoid((x_t @ self.W_xi) + (h @ self.W_hi) + self.b_i)
# Forget gate
f_t = torch.sigmoid((x_t @ self.W_xf) + (h @ self.W_hf) + self.b_f)
# Cell gate
g_t = torch.tanh((x_t @ self.W_xc) + (h @ self.W_hc) + self.b_c)
# Update cell state
c_t = f_t * c + i_t * g_t
# Output gate
o_t = torch.sigmoid((x_t @ self.W_xo) + (h @ self.W_ho) + self.b_o)
# Update hidden state
h_t = o_t * torch.tanh(c_t)
# Output
y_t = h_t @ self.W_hy + self.b_y
outputs.append(y_t)
h = h_t
c = c_t
outputs = torch.stack(outputs, dim=1) # (batch_size, seq_len, output_dim)
return outputs, (h, c)
def init_hidden(self, batch_size):
return (torch.zeros(batch_size, self.hidden_dim, device=self.device),
torch.zeros(batch_size, self.hidden_dim, device=self.device))
39.Transformer 的基本结构是什么?
Transformer 的基本结构由以下几个核心模块组成,主要应用于自然语言处理、图像理解等领域:
Transformer 基本结构(以 Encoder 为例):
-
输入嵌入(Input Embedding)
- 将离散的词 token 转换为向量表示,通常加上 Positional Encoding(位置编码)以注入顺序信息。
-
多头自注意力机制(Multi-Head Self-Attention)
- 并行计算多个不同的注意力头,每个头分别学习不同的表示子空间:
Attention(Q, K, V) = softmax(QKᵀ / √dₖ) V - Q(query)、K(key)、V(value)都来自同一个输入。
- 并行计算多个不同的注意力头,每个头分别学习不同的表示子空间:
-
残差连接 & LayerNorm(Add & Norm)
- 将 Attention 输出加到原始输入上,再进行 LayerNorm:
x = LayerNorm(x + Attention(x))
- 将 Attention 输出加到原始输入上,再进行 LayerNorm:
-
前馈神经网络(Feed Forward Network)
- 每个位置独立的两层 MLP:
FFN(x) = max(0, xW₁ + b₁)W₂ + b₂ - 通常使用 ReLU 或 GELU 激活函数。
- 每个位置独立的两层 MLP:
-
残差连接 & LayerNorm(再次 Add & Norm)
- x = LayerNorm(x + FFN(x))
多个这样的 Encoder Block 可堆叠构成完整 Encoder。
Decoder 结构类似,但每个块有两次 Attention:
- 第一次是 Masked Self-Attention(防止看到未来信息)
- 第二次是 Encoder-Decoder Attention(Q 来自 Decoder,K/V 来自 Encoder 输出)
总体结构:
Encoder:
Input → Embedding + PosEncoding → [Encoder Block × N] → Output
Decoder:
Target → Embedding + PosEncoding → [Decoder Block × N] → Linear → Softmax
transformer
import torch.nn as nn
import torch.nn.functional as F
import math
class SimpleSelfAttention(nn.Module):
def __init__(self, embed_dim, num_heads):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
if embed_dim % num_heads != 0:
raise ValueError(f"embedding dimension = {embed_dim} should be divisible by number of heads = {num_heads}")
self.head_dim = embed_dim // num_heads
self.W_q = nn.Linear(embed_dim, embed_dim)
self.W_k = nn.Linear(embed_dim, embed_dim)
self.W_v = nn.Linear(embed_dim, embed_dim)
self.W_o = nn.Linear(embed_dim, embed_dim)
def scaled_dot_product_attention(self, Q, K, V, mask=None):
B, nQ, H, dK = Q.shape
_, nK, _, dV = V.shape
energies = torch.einsum('bqhd, bkhd->bhqk', Q, K) / math.sqrt(dK)
if mask is not None:
energies = energies.masked_fill(mask == 0, float('-inf'))
attention = F.softmax(energies, dim=-1)
out = torch.einsum('bhqk, bkhd->bqhd', attention, V).reshape(B, nQ, self.embed_dim)
return self.W_o(out), attention
def split_heads(self, x, batch_size):
return x.view(batch_size, -1, self.num_heads, self.head_dim).permute(0, 1, 2, 3) # (B, seq_len, num_heads, head_dim)
def forward(self, x, mask=None):
batch_size, seq_len, embed_dim = x.shape
Q = self.split_heads(self.W_q(x), batch_size) # (B, seq_len, num_heads, head_dim)
K = self.split_heads(self.W_k(x), batch_size) # (B, seq_len, num_heads, head_dim)
V = self.split_heads(self.W_v(x), batch_size) # (B, seq_len, num_heads, head_dim)
out, attention = self.scaled_dot_product_attention(Q, K, V, mask)
return out, attention
# 2. 简单 Feed-Forward 网络:
class SimpleFeedForward(nn.Module):
def __init__(self, embed_dim, ffn_hidden_dim):
super().__init__()
self.fc1 = nn.Linear(embed_dim, ffn_hidden_dim)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(ffn_hidden_dim, embed_dim)
def forward(self, x):
return self.fc2(self.relu(self.fc1(x)))
# 3. 简化版 Transformer Block (Encoder):
class SimpleTransformerBlock(nn.Module):
def __init__(self, embed_dim, num_heads, ffn_hidden_dim, dropout):
super().__init__()
self.attention = SimpleSelfAttention(embed_dim, num_heads)
self.norm1 = nn.LayerNorm(embed_dim)
self.feed_forward = SimpleFeedForward(embed_dim, ffn_hidden_dim)
self.norm2 = nn.LayerNorm(embed_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, x, mask=None):
# Self-Attention
attention_output, _ = self.attention(x, mask)
# Residual connection and Layer Normalization
norm1_output = self.norm1(x + self.dropout(attention_output))
# Feed-Forward
ff_output = self.feed_forward(norm1_output)
# Residual connection and Layer Normalization
output = self.norm2(norm1_output + self.dropout(ff_output))
return output
# 4. 简单的 Transformer Encoder:
class SimpleTransformerEncoder(nn.Module):
def __init__(self, num_layers, embed_dim, num_heads, ffn_hidden_dim, dropout, vocab_size, max_len):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embed_dim)
self.pos_embedding = nn.Embedding(max_len, embed_dim)
self.layers = nn.ModuleList([
SimpleTransformerBlock(embed_dim, num_heads, ffn_hidden_dim, dropout)
for _ in range(num_layers)
])
self.dropout = nn.Dropout(dropout)
self.max_len = max_len
def forward(self, x, mask=None):
batch_size, seq_len = x.shape
positions = torch.arange(0, seq_len).unsqueeze(0).expand(batch_size, seq_len).to(x.device)
x = self.dropout(self.embedding(x) + self.pos_embedding(positions))
for layer in self.layers:
x = layer(x, mask)
return x
位置编码
位置编码(Positional Encoding) 是一种用于引入词语位置信息的机制,应用于 Transformer 模型中,以补偿模型缺乏顺序感知能力的缺陷。
Learnable Position Embedding(可学习位置编码)
import torch
import torch.nn as nn
class LearnablePositionalEncoding(nn.Module):
def __init__(self, max_len, d_model):
super().__init__()
# 定义 max_len 个位置的可学习位置向量
self.pos_embedding = nn.Parameter(torch.zeros(1, max_len, d_model))
nn.init.xavier_uniform_(self.pos_embedding) # 初始化更有效
def forward(self, x):
"""
x: [batch_size, seq_len, d_model]
"""
seq_len = x.size(1)
# 截取当前输入序列长度对应的部分位置向量
return x + self.pos_embedding[:, :seq_len, :]
正余弦函数的编码
Relative Position Encoding(相对位置编码)
Rotary Position Embedding(RoPE):用于 LLaMA、ChatGLM 等,增强了旋转不变性
Bert
import torch
import torch.nn as nn
import math
class BertEmbedding(nn.Module):
def __init__(self, vocab_size, embed_size, max_len=512, type_vocab_size=2):
super().__init__()
self.token_embed = nn.Embedding(vocab_size, embed_size)
self.position_embed = nn.Embedding(max_len, embed_size)
self.segment_embed = nn.Embedding(type_vocab_size, embed_size)
self.layer_norm = nn.LayerNorm(embed_size)
def forward(self, input_ids, token_type_ids):
seq_len = input_ids.size(1)
position_ids = torch.arange(seq_len, dtype=torch.long, device=input_ids.device).unsqueeze(0).expand_as(input_ids)
embeddings = self.token_embed(input_ids) + self.position_embed(position_ids) + self.segment_embed(token_type_ids)
return self.layer_norm(embeddings)
class MultiHeadSelfAttention(nn.Module):
def __init__(self, embed_size, num_heads):
super().__init__()
assert embed_size % num_heads == 0
self.num_heads = num_heads
self.head_dim = embed_size // num_heads
self.query = nn.Linear(embed_size, embed_size)
self.key = nn.Linear(embed_size, embed_size)
self.value = nn.Linear(embed_size, embed_size)
self.out = nn.Linear(embed_size, embed_size)
def forward(self, x, mask=None):
B, T, C = x.size()
q = self.query(x).view(B, T, self.num_heads, self.head_dim).transpose(1, 2)
k = self.key(x).view(B, T, self.num_heads, self.head_dim).transpose(1, 2)
v = self.value(x).view(B, T, self.num_heads, self.head_dim).transpose(1, 2)
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(self.head_dim)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
attn = torch.softmax(scores, dim=-1)
context = torch.matmul(attn, v).transpose(1, 2).contiguous().view(B, T, C)
return self.out(context)
class FeedForward(nn.Module):
def __init__(self, embed_size, hidden_size):
super().__init__()
self.net = nn.Sequential(
nn.Linear(embed_size, hidden_size),
nn.GELU(),
nn.Linear(hidden_size, embed_size),
)
def forward(self, x):
return self.net(x)
class TransformerBlock(nn.Module):
def __init__(self, embed_size, num_heads, ff_hidden_size):
super().__init__()
self.attn = MultiHeadSelfAttention(embed_size, num_heads)
self.norm1 = nn.LayerNorm(embed_size)
self.ff = FeedForward(embed_size, ff_hidden_size)
self.norm2 = nn.LayerNorm(embed_size)
def forward(self, x, mask=None):
attn_output = self.attn(x, mask)
x = self.norm1(x + attn_output)
ff_output = self.ff(x)
return self.norm2(x + ff_output)
class BertModel(nn.Module):
def __init__(self, vocab_size, embed_size=768, num_heads=12, ff_hidden_size=3072, num_layers=12, max_len=512):
super().__init__()
self.embedding = BertEmbedding(vocab_size, embed_size, max_len)
self.layers = nn.ModuleList([
TransformerBlock(embed_size, num_heads, ff_hidden_size) for _ in range(num_layers)
])
self.pooler = nn.Linear(embed_size, embed_size)
self.activation = nn.Tanh()
def forward(self, input_ids, token_type_ids, attention_mask=None):
x = self.embedding(input_ids, token_type_ids)
for layer in self.layers:
x = layer(x, attention_mask)
# 取 [CLS] token 的输出作为 pooled output
cls_token = x[:, 0]
pooled = self.activation(self.pooler(cls_token))
return x, pooled # sequence_output, pooled_output
Embedding 层是什么
class Embedding(nn.Module):
def __init__(self, num_embeddings, embedding_dim):
self.weight = nn.Parameter(torch.randn(num_embeddings, embedding_dim))
def forward(self, input_ids):
return self.weight[input_ids]
GPT 模型
import torch
import torch.nn as nn
import torch.nn.functional as F
class GPTConfig:
def __init__(self, vocab_size, block_size, n_layer, n_head, n_embd):
self.vocab_size = vocab_size
self.block_size = block_size # 序列最大长度
self.n_layer = n_layer # Transformer 层数
self.n_head = n_head # 注意力头数
self.n_embd = n_embd # 嵌入维度
class CausalSelfAttention(nn.Module):
def __init__(self, config):
super().__init__()
assert config.n_embd % config.n_head == 0
self.key = nn.Linear(config.n_embd, config.n_embd)
self.query = nn.Linear(config.n_embd, config.n_embd)
self.value = nn.Linear(config.n_embd, config.n_embd)
self.proj = nn.Linear(config.n_embd, config.n_embd)
self.n_head = config.n_head
self.dropout = nn.Dropout(0.1)
self.register_buffer("mask", torch.tril(torch.ones(config.block_size, config.block_size))
.unsqueeze(0).unsqueeze(0)) # [1, 1, T, T]
def forward(self, x):
B, T, C = x.size()
head_dim = C // self.n_head
q = self.query(x).view(B, T, self.n_head, head_dim).transpose(1, 2) # [B, nh, T, hs]
k = self.key(x).view(B, T, self.n_head, head_dim).transpose(1, 2)
v = self.value(x).view(B, T, self.n_head, head_dim).transpose(1, 2)
att = (q @ k.transpose(-2, -1)) / (head_dim ** 0.5) # [B, nh, T, T]
att = att.masked_fill(self.mask[:, :, :T, :T] == 0, float("-inf"))
att = F.softmax(att, dim=-1)
att = self.dropout(att)
y = att @ v # [B, nh, T, hs]
y = y.transpose(1, 2).contiguous().view(B, T, C) # concat heads
return self.proj(y)
class TransformerBlock(nn.Module):
def __init__(self, config):
super().__init__()
self.ln1 = nn.LayerNorm(config.n_embd)
self.attn = CausalSelfAttention(config)
self.ln2 = nn.LayerNorm(config.n_embd)
self.ff = nn.Sequential(
nn.Linear(config.n_embd, 4 * config.n_embd),
nn.GELU(),
nn.Linear(4 * config.n_embd, config.n_embd),
nn.Dropout(0.1)
)
def forward(self, x):
x = x + self.attn(self.ln1(x)) # 残差连接
x = x + self.ff(self.ln2(x)) # 残差连接
return x
class GPT(nn.Module):
def __init__(self, config):
super().__init__()
self.token_embed = nn.Embedding(config.vocab_size, config.n_embd)
self.pos_embed = nn.Embedding(config.block_size, config.n_embd)
self.blocks = nn.Sequential(*[TransformerBlock(config) for _ in range(config.n_layer)])
self.ln_f = nn.LayerNorm(config.n_embd)
self.head = nn.Linear(config.n_embd, config.vocab_size, bias=False)
self.block_size = config.block_size
def forward(self, idx, targets=None):
B, T = idx.shape
assert T <= self.block_size
tok_emb = self.token_embed(idx)
pos = torch.arange(0, T, device=idx.device).unsqueeze(0)
pos_emb = self.pos_embed(pos)
x = tok_emb + pos_emb
x = self.blocks(x)
x = self.ln_f(x)
logits = self.head(x)
if targets is None:
return logits, None
else:
loss = F.cross_entropy(logits.view(-1, logits.size(-1)), targets.view(-1))
return logits, loss
| 方法 | 每步用的数据量 | 优点 | 缺点 |
|---|---|---|---|
| Batch GD | 全部样本 | 梯度方向准确稳定 | 计算慢,内存大 |
| SGD | 单个样本 | 速度快,跳出局部极小 | 收敛震荡,噪声较大 |
| Mini-batch GD | 小批量样本 | 速度稳定,训练效率好 | 需要调节 batch size |
这是一个非常常见也非常重要的面试题。**类别不均衡(class imbalance)**问题在真实世界中经常发生,尤其是金融欺诈检测、医疗诊断、推荐系统等领域。
如何处理类别不均衡问题?
一句话概括:
类别不均衡可以通过 数据层处理(采样、数据增强)、模型层处理(损失函数、类别权重)、评估指标选择 三个维度来缓解。
1.1 过采样(Over-sampling)——让少数类更多
- 重复复制少数类样本,或使用 SMOTE、ADASYN 等合成新样本;
- 适合小样本、简单数据;
- 缺点:可能过拟合、增加训练时间。
1.2 欠采样(Under-sampling)——减少多数类样本
- 随机丢弃一部分多数类样本;
- 快速有效,但可能丢失重要信息。
1.3 数据增强(Augmentation)
- 对少数类使用数据增强(如图像翻转、旋转、扰动等)生成更多样本;
- 保持数据多样性,降低过拟合风险。
2. 模型层处理方法(更稳定)
2.1 类别加权损失(Class Weights)
- 在
CrossEntropyLoss中设置weight参数,少数类权重高:
loss_fn = nn.CrossEntropyLoss(weight=torch.tensor([0.2, 0.8]))
- 或使用
BCEWithLogitsLoss(pos_weight=...)处理二分类。
2.2 Focal Loss(聚焦难样本)
- 经典解决不均衡问题的损失函数,常用于目标检测(如 RetinaNet):
FL(p_t) = -α_t * (1 - p_t)^γ * log(p_t)
- γ 控制聚焦程度,α 控制类别平衡。
2.3 自定义采样器
- 在 PyTorch 中使用
WeightedRandomSampler按类别频率采样样本。
3. 模型评估指标选择(面试加分项)
不推荐用 Accuracy,因为:
类别极度不平衡时,模型只预测多数类也能“高准确率”。
推荐使用:
- Precision / Recall / F1-score
- ROC-AUC / PR-AUC
- Confusion Matrix(可视化分析)
- Cohen's Kappa、Matthews Correlation Coefficient
🔍 实战举例(极端样本比例:正类 1%,负类 99%)
| 方法 | 效果 |
|---|---|
| 只用原始数据训练 | 准确率高,但 Recall = 0 |
| 过采样少数类 | Recall 提升,但可能过拟合 |
| Focal Loss | 模型关注难分类样本,表现更稳定 |
| PR-AUC 评估 | 更合理体现模型对正类的检测能力 |
面试总结金句:
面对类别不均衡问题,首先可以通过采样和数据增强增加少数类样本,其次在模型训练时使用加权损失函数或 Focal Loss 来聚焦难分类样本,最后评估时要避免使用 accuracy,而应选择 F1、Recall、PR-AUC 等指标。
深度学习评价指标
| 实际/预测 | 预测为正类 | 预测为负类 |
|---|---|---|
| 实际为正类 | TP | FN |
| 实际为负类 | FP | TN |
这些值是分类性能指标(如准确率、精确率、召回率、F1 分数)的基础:
- 准确率 Accuracy = \(\frac{TP + TN}{TP + TN + FP + FN}\)
- 精确率 Precision = \(\frac{TP}{TP + FP}\)
- 召回率 Recall = \(\frac{TP}{TP + FN}\)
- F1 分数 = \(2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号