白话 RLHF

2. 状态价值（State Value）

状态价值 \(V_\pi(s)\) 表示在策略 \(\pi\) 下，从状态 \(s\) 开始的预期回报（Expected Return）。

\[V_\pi(s) = \mathbb{E}_{A_t, S_{t+1}, \ldots} \left[ U_t | S_t = s \right] \]

\[[ V_\pi(s) = \sum_{a \in A} \pi(a|s) \sum_{s' \in S} P(s'|s,a) \left[ R(s,a,s') + \gamma \cdot V_\pi(s') \right] ] \]

其中：
\(\pi(a|s)\) 是策略 \(\pi\) 在状态 (s) 下选择动作 (a) 的概率。
\(P(s'|s,a)\) 是从状态 (s) 采取动作 (a) 转移到状态 (s') 的概率。
\(R(s,a,s')\) 是从状态 (s) 采取动作 (a) 转移到状态 (s') 的即时奖励。
\(\gamma\) 是折扣因子，取值范围为 ([0, 1])，用于衡量未来奖励的重要性。
\(V_\pi(s')\) 是在状态 (s') 下按照策略 (\pi) 继续行动的期望回报。

累积回报（Cumulative Reward）的表达

\[U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots \]

这里的 \(U_t\) 是从时间步 \(t\) 开始的累积回报（Cumulative Reward）。
表达式逐步展开为：

\[V_\pi(s) = \mathbb{E}_{A_t, S_{t+1}, \ldots} \left[ R_t + \gamma U_{t+1} | S_t = s \right] \]

因此，状态价值可以写为：

\[ V_\pi(s) = \mathbb{E}_{A_t, S{t+1}, \ldots} \left[ R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots \mid S_t = s \right] \]

策略梯度（Policy Gradient)

1. Policy Gradient 的基本概念
   策略梯度方法是一种直接优化策略（Policy）的方法，目标是找到一个最优策略 \(\pi^*\)，使得长期回报（Return）最大化。

策略函数 \(\pi(\cdot | s; \theta)\)

定义：策略函数 \(\pi(a | s; \theta)\) 表示在状态 ( s ) 下选择动作 ( a ) 的概率，参数 \(\theta\)用于调整这个概率分布。
实现：通常使用神经网络（NN）来表示策略函数，输出经过 SoftMax 层转换为概率分布。

目标函数 \((\theta)\)

目标函数 \(J(\theta)\) 定义为从初始状态 \(S_0\) 开始的期望回报：
\(J(\theta) = \mathbb{E}_{S} \left[ V_\pi(S) \right] = \mathbb{E}{\tau \sim p_\theta(\tau)} \left[ \sum_{t} \gamma^t r(s_t, a_t) \right]\)
其中：
\(V_\pi(S)\) 是在策略 \(\pi\) 下状态 ( S ) 的价值（Value）。
\(\tau\) 是一个轨迹（Trajectory），即一系列状态和动作的序列：\(\tau = (s_0, a_0, s_1, a_1, \ldots)\)。
\(p_\theta(\tau)\) 是在策略 \(\pi_\theta\) 下生成轨迹 \(\tau\) 的概率。
$\gamma $ 是折扣因子（Discount Factor），用于衡量未来奖励的重要性。
\(r(s_t, a_t)\) 是在状态 \(s_t\) 采取动作 \(a_t\)后获得的即时奖励（Immediate Reward）。
期望优化参数最大化 ![max J()]

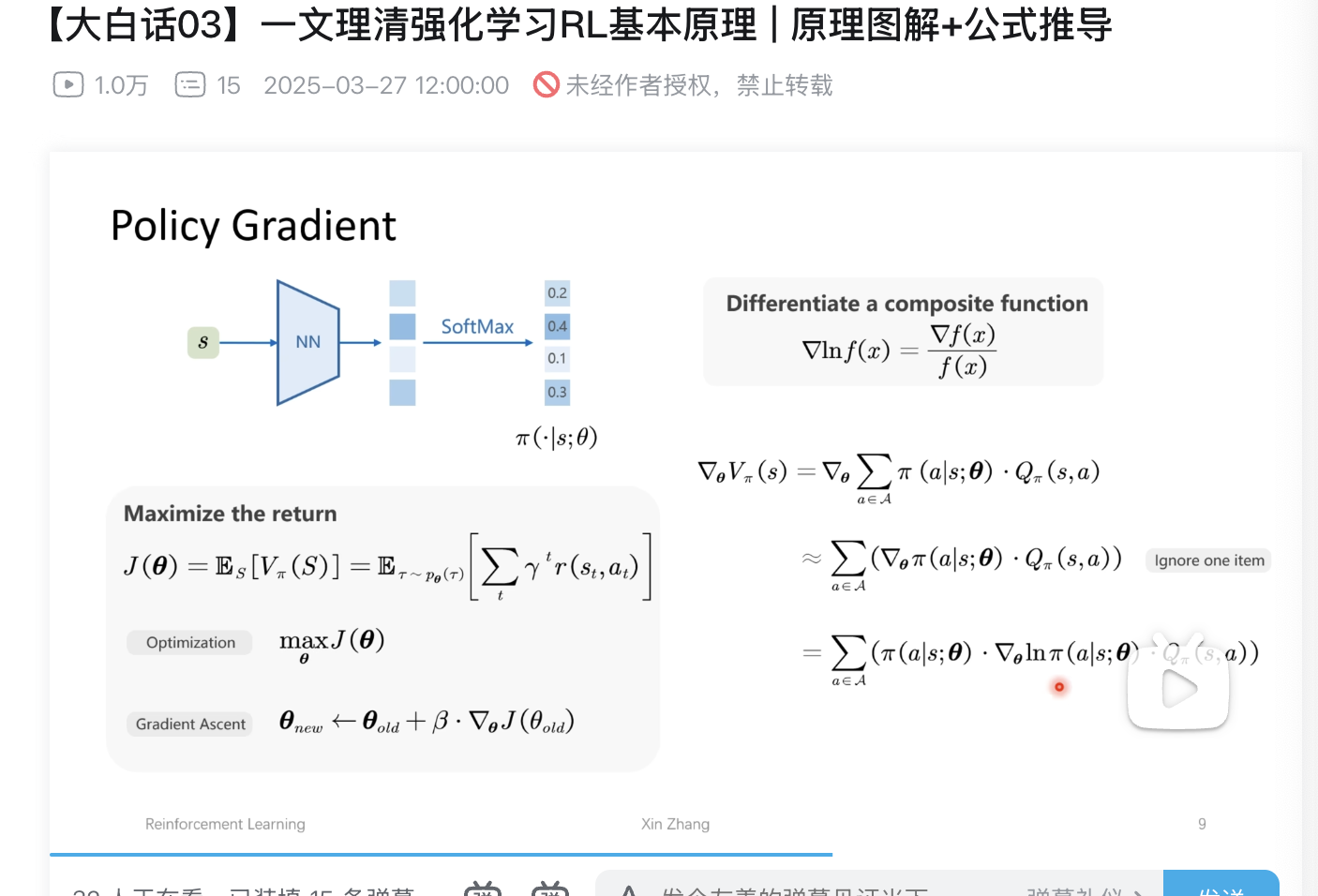
首先看复合函数公式

\[ \nabla \ln f(x) = \frac{\nabla f(x)}{f(x)} \]

2. 策略价值函数对参数的梯度
   接下来，我们来分析策略价值函数 \(V_\pi(s)\) 对参数 \(\theta\) 的梯度：

\[ \nabla_\theta V_\pi(s) = \nabla_\theta \sum_{a \in \mathcal{A}} \pi(a | s; \theta) \cdot Q_\pi(s, a) \]

这个公式表示在状态 \((s)\) 下，策略价值函数 \(V_\pi(s)\) 对参数 \(\theta\) 的梯度。具体解释如下：
\(V_\pi(s)\)：表示在策略 \(\pi\) 下状态 ( s ) 的价值（Value）。
\(\pi(a | s; \theta)\)：表示在状态 ( s ) 下选择动作 ( a ) 的概率，参数为 \(\theta\)。
\(Q_\pi(s, a)\)：表示在策略 \(\pi\) 下，从状态 ( s ) 采取动作 ( a ) 后的行动价值（Action Value）。
\(\sum_{a \in \mathcal{A}}\)：对所有可能的动作 ( a ) 进行求和。

奖励函数优化为

\[ \nabla_\theta V_\pi(s) = \nabla_\theta \sum_{a \in \mathcal{A}} \pi(a | s; \theta) \cdot Q_\pi(s, a) \]

在某些情况下（例如在策略梯度定理的推导中），可以忽略第二项（即 \(( \pi(a | s; \theta) \cdot \nabla_\theta Q_\pi(s, a) )）\)，
得到简化形式：

\[\nabla_\theta V_\pi(s) \approx \sum_{a \in \mathcal{A}} \left( \nabla_\theta \pi(a | s; \theta) \cdot Q_\pi(s, a) \right) \]

\[ \nabla_\theta J(\theta) = \mathbb{E}{\tau \sim p\theta(\tau)} \left[ \sum_{t} \nabla_\theta \ln \pi(a_t | s_t; \theta) \cdot R(\tau) \right] \]

3. 对数似然性的引入

• 简化梯度计算：直接对 \((\pi(a|s; \theta))\) 求导可能会非常复杂，而对其对数形式 \((\ln \pi(a|s; \theta))\) 求导则相对简单。
• 数学性质：对数函数的导数具有良好的数学性质，例如 \((\nabla \ln f(x) = \frac{\nabla f(x)}{f(x)})\)，这在优化过程中非常有用。

加入对数似然之后的公式

\[[ \nabla_\theta V_\pi(s) = \sum_{a \in \mathcal{A}} \left( \pi(a|s; \theta) \cdot \nabla_\theta \ln \pi(a|s; \theta) \cdot Q_\pi(s, a) \right) ] \]

1. 优化目标

\[[ \boxed{\max_{\boldsymbol{\theta}} J(\boldsymbol{\theta})} ] \]

2. 梯度上升更新规则

\[ \boxed{\boldsymbol{\theta}{\text{new}} \leftarrow \boldsymbol{\theta}{\text{old}} + \beta \cdot \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}_{\text{old}})} \]

3. 带有动作价值函数的梯度上升更新规则

\[ \boxed{\boldsymbol{\theta}{\text{new}} \leftarrow \boldsymbol{\theta}{\text{old}} + \beta \cdot Q_{\pi}(s, a) \cdot \nabla_{\boldsymbol{\theta}} \ln \pi(a|s; \boldsymbol{\theta}_{\text{old}})} \]

REINFORCE 和 Actor-Critic

1. REINFORCE

REINFORCE 是一种基于策略梯度的方法，用于解决强化学习问题。其核心思想是直接优化策略函数 \((\pi(a|s; \theta))\)，以最大化期望回报 \((J(\theta))\)。

主要组成部分：

• 优化目标：

\[ \max_{\theta} J(\theta) \]

其中 \((J(\theta))\) 是关于参数 \((\theta)\) 的性能指标（例如，期望累积奖励）。

• 梯度上升更新规则：

\[ \theta_{\text{new}} \leftarrow \theta_{\text{old}} + \beta \cdot \nabla_{\theta} J(\theta_{\text{old}}) \]

这里 \((\beta)\) 是学习率，\((\nabla_{\theta} J(\theta_{\text{old}}))\) 是性能指标 \((J(\theta))\) 关于 \((\theta)\) 的梯度。

• 具体更新公式：

\[ \theta_{\text{new}} \leftarrow \theta_{\text{old}} + \beta \cdot Q_{\pi}(s, a) \cdot \nabla_{\theta} \ln \pi(a|s; \theta_{\text{old}}) \]

其中 \((Q_{\pi}(s, a))\) 是在策略 \((\pi)\) 下状态 \((s)\) 和动作 \((a)\) 的动作价值函数。

• 回报计算：

\[ u_t = \sum_{k=t}^{n} \gamma^{k-t} \cdot r_k \]

这表示从时间步 (t) 到终止状态的累积折扣奖励。

• 参数更新：

\[ \theta_{\text{new}} \leftarrow \theta_{\text{old}} + \beta \cdot \sum_{t=1}^{n} \gamma^{t-1} \cdot u_t \cdot \nabla_{\theta} \ln \pi(a_t|s_t; \theta_{\text{old}}) \]

这是在整个轨迹上进行参数更新的表达式。

2. Baseline（基准线）

为了减少方差，REINFORCE 方法通常会引入一个 Baseline（基准线）

\((b)\)：

\[\mathbb{E}_{S} \left[ \mathbb{E}_{A \sim \pi(\cdot|S; \theta)} \left[ (Q_{\pi}(S, A) - b) \cdot \nabla_{\theta} \ln \pi(A|S; \theta) \right] \right] \]

这里的 (b) 可以是状态值函数 (V_{\pi}(s))，它是一个与动作无关的估计值，用于调整动作价值 (Q_{\pi}(s, a))。

3. Actor-Critic

Actor-Critic 方法结合了 值函数方法 和 策略梯度方法 的优点，分别使用 Actor（执行者）和 Critic（批评者）两个组件。

主要组成部分：

• Actor（执行者）：

  • 负责根据当前策略 \((\pi(a|s; \theta))\) 选择动作 \((a)\)。
  • 通过 \((\epsilon-\text{greedy})\) 策略进行探索。

• Critic（批评者）：

  • 评估 Actor 所采取动作的好坏，即计算动作价值 \((Q_{\pi}(s, a))\)。
  • 根据环境反馈（奖励 (r) 和下一个状态 (s')）来更新其对动作价值的估计。

• 更新过程：

  1. Actor 更新：根据 Critic 提供的动作价值信息来更新策略参数 $(\theta)$。
  2. Critic 更新：根据环境反馈来更新动作价值函数 \(Q_{\pi}(s, a)\) 的参数。

• 网络结构：

  • 使用神经网络（NN）来近似动作价值函数 (Q_{\pi}(s, a))。
  • 输入为状态 (s) 和动作 (a)，输出为动作价值 (Q_{\pi}(s, a))。

Trust Region Policy Optimization (TRPO) 解析

1. TRPO 的基本思想
   TRPO 的核心思想是在每次迭代中，通过在“信任区域”内进行策略更新来保证性能的单调提升。具体来说，它试图找到一个新策略 \((\pi_{\theta'})\) ，使得其与旧策略 \((\pi_{\theta})\) 在一定范围内（即信任区域内）进行更新，同时最大化目标函数 \((J(\theta))\)（通常为期望累积奖励）。
2. 目标函数的表达
   TRPO 的目标是最大化新策略 \((pi_{\theta'})\) 相对于旧策略 \((\pi_{\theta})\) 的性能提升，即 \((J(\theta') - J(\theta))\)。
   \([ J(\theta') - J(\theta) = \mathbb{E}{\tau \sim p{\theta'}(\tau)} \left[ \sum_{t=0}^{\infty} \gamma^t A_{\pi_{\theta}}(s_t, a_t) \right] ]\)
   这里 \((A_{\pi_{\theta}}(s_t, a_t))\) 是在旧策略 \((\pi_{\theta})\) 下的状态-动作优势函数。
3. 状态分布不变假设
   为了简化上述表达式，TRPO 做了第一个近似：忽略状态分布的变化。
   即假设新策略 \((\pi_{\theta'})\) 和旧策略 \((\pi_{\theta})\) 生成的轨迹 \((\tau)\) 在状态分布上没有显著差异，因此可以写作：
   \([ J(\theta') - J(\theta) \approx \mathbb{E}{s_t \sim p{\theta}(s_t)} \left[ \mathbb{E}{a_t \sim \pi{\theta'}(a_t | s_t)} \left[ \gamma^t \cdot A_{\pi_{\theta}}(s_t, a_t) \right] \right] ]\)