斐波那契数列【转】
斐波那契数列
以下内容来自维基百科http://zh.wikipedia.org/wiki/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97
维基百科更全,但经过几次都发现易出现不能显示的问题,如果需要可以参考百度百科http://baike.baidu.com/view/816.htm
1、通项公式:

2、推导
初等代数解法
已知
首先构建等比数列
设
化简得
比较系数可得:
不妨设
解得:

所以有 , 即
, 即 为等比数列。
为等比数列。
求出数列{ }
}
由以上可得:
变形得: 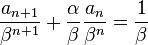 。 令
。 令
求数列{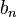 }进而得到{
}进而得到{ }
}

设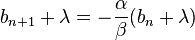 ,解得
,解得 。 故数列
。 故数列  为等比数列
为等比数列
即  。而
。而  , 故有
, 故有 
又有 和
和 
可得 ![a_{n}=\frac{\sqrt{5}}{5} \cdot \left[\left(\frac{1 + \sqrt{5}}{2}\right)^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right]](http://upload.wikimedia.org/math/c/6/d/c6dc35b68545005b9b6fa6995c4f6d52.png)
得出  表达式
表达式
![a_{n}=\frac{\sqrt{5}}{5} \cdot \left[\left(\frac{1 + \sqrt{5}}{2}\right)^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right]](http://upload.wikimedia.org/math/c/6/d/c6dc35b68545005b9b6fa6995c4f6d52.png)
线性代数解法


构建一个矩阵方程
设Jn为第n个月有生育能力的兔子数量,An为这一月份的兔子数量。
上式表达了两个月之间,兔子数目之间的关系。而要求的是,An+1的表达式。
求矩阵的特征值:
行列式:- *(1-
*(1- )-1*1=
)-1*1= 2-
2- -1
-1
当行列式的值为0,解得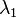 =
= 或
或 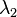 =
=
特征矢量
将两个特征值代入
求特征矢量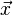 得
得
 =
=
 =
=
分解首矢量
第一个月的情况是兔子一对,新生0对。
将它分解为用特征矢量表示。
 (4)
(4)
用数学归纳法证明
从
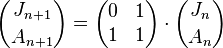 =
=
可得
 (5)
(5)
化简矩阵方程
将(4) 代入 (5)
根据 3
求A的表达式
现在在6的基础上,可以很快求出An+1 的表达式,将两个特征值代入 6 中
 (7)
(7)
(7)即为An+1 的表达式
近似值
3、斐波那契数列与黄金分割点间的不解之缘
开普勒发现数列前、后两项之比1/2 ,2/3 , 3/5 ,5/8 ,8/13 ,13/21 ,21/34 ,...... ,也组成了一个数列,会趋近黄金分割:

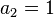
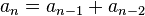

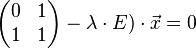

![{J_{n+1}\choose A_{n+1}} = \lambda^n \cdot [\frac{1}{\sqrt{5}} \cdot \begin{pmatrix}1\\\frac{1}{2} (1 + \sqrt{5})\end{pmatrix}-\frac{1}{\sqrt{5}} \cdot \begin{pmatrix}1\\\frac{1}{2} (1 - \sqrt{5})\end{pmatrix}]](http://upload.wikimedia.org/math/6/a/0/6a08087a30d1e00382906c2e829ad4e6.png)




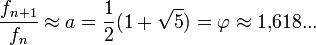

 浙公网安备 33010602011771号
浙公网安备 33010602011771号