刘宇波老师leetcode刷题系列
刘宇波老师leetcode刷题系列

1. 算法面试到底是什么鬼?
一提起算法面试,很多同学就会心有余悸。可其实,大多数企业的算法面试,并没有那么可怕。并不是一定要啃完整本《算法导论》,才能玩儿转算法面试;也并不是只有ACM参赛选手,才能笑傲算法面试。恰恰相反,大多数算法面试关注的算法思维,其实很基础。在这一章,和大家聊一聊,算法面试,到底是什么鬼?...
1-1 算法面试不仅仅是正确的回答问题
课程的目标是什么?让大家在面试中的算法问题,有一个合理的思考路径
1-2 算法面试只是面试的一部分
我们需要对一组数据进行排序
快速排序算法O(nlogn)?
我们可以跟面试官讨论
- 这组数据有什么样的特征?
- 有没有可能包含有大量重复的元素?
- 如果有这种可能的话,三路快排是更好的选择
- 是否大部分数据距离它正确的位置更近,是否近乎有效
- 是否数据的取值范围非常有限,比如对学生成绩排序,如果是这样的话,计数排序是更好的选择
对排序有没有额外的要求?
- 是否需要稳定排序
- 如果是的话,归并排序是更好的选择
数据的存储状况是怎样的?
- 是否使用链表存储的?
- 数据的大小是否可以装载内存中?
- 数据量很大,或者内存很小不足以装载在内存里,需要使用外部排序算法
1-3 如何准备算法面试
项目经历和项目中遇到的实际问题
你遇到的印象最深的bug是什么?
面向对象
设计模式
网络相关;安全相关,内存相关,并发相关,系统设计,scalability
关于过去:参与项目至关重要
如何找到项目?
- 实现
- 参与实战课程学习
- 慕课网
- 创建自己的项目
- 自己做小应用:计划表;备忘录;播放器...
- 自己解决小问题:爬虫;数据分析;词频统计...
- "不是项目"的项目:一本优秀的技术书籍的代码整理
- 分享:自己的技术博客;github等等
通过过去了解你的思考行为方式
- 遇到过的最大挑战?
- 犯过的错误?
- 遭遇的失败?
- 最享受的工作内容?
- 遇到冲突的处理方式?
- 做的最与众不同的事?
准备好合适的问题问面试官
- 整个小组的大概运行模式是怎样的
- 整个项目的后续规划是如何的?
- 这个产品中的某个问题是如何解决的?
- 如何会选择某种技术?标准?
- 我对某个技术很感兴趣,在你的小组中我会有怎样的机会深入这种技术?
1-4 如何回答算法面试问题
算法面试的准备范围
- 不要轻视基础算法和数据结构,而只关注"有意思"的题目
- 各种排序算法
- 基础数据结构和算法的实现:如堆,二叉树,图
- 基础数据结构的使用:如链表.栈,队列,哈希表,图,Trie,并查集....
- 基础算法:深度优先;广度优先;二分查找,递归....
- 基础算法思想:递归,分治,回溯搜索,贪心,动态规划
解决算法面试问题的整体思路
-
注意题目中的条件
-
题目中的一些暗示
有一些题目中的条件就是暗示
- 设计一个O(nlogn)的算法
- 无需考虑额外的空间
- 数据规模大概是10000
-
假如一下子没有思路的话
- 自己先测试几个简单的测试用例,试验一下
- 不要忽视暴力算法
-
我们可以看到一个例题,就是leetcode第三题
给定一个字符串,请你找出其中不含有重复字符的 **最长子串** 的长度。
这个题目到我们没有思路的时候,我们可以使用暴力法进行计算,在一个字符串中寻找没有重复字母的最长子串
-
对于字符串s的子串s[i...j]
-
使用O(n^2)的算法遍历i,j,可以的到的最大子串S[i,j];
- 我们再使用O(length((s[i.....j]))的算法判断s[i....j]中是否含有重复字母
-
这种算法的时间复杂度为O(n^3),对于n=100的数据
第2章 面试中的复杂度分析
很多同学一提起复杂度分析就头疼,马上想起了《算法导论》中复杂的数学推导。但其实在一般的企业面试中,对复杂度的分析要求并没有那么高,但也是绕不过去的坎儿。在这一章,和大家介绍一下,面试中需要掌握的复杂度分析。...
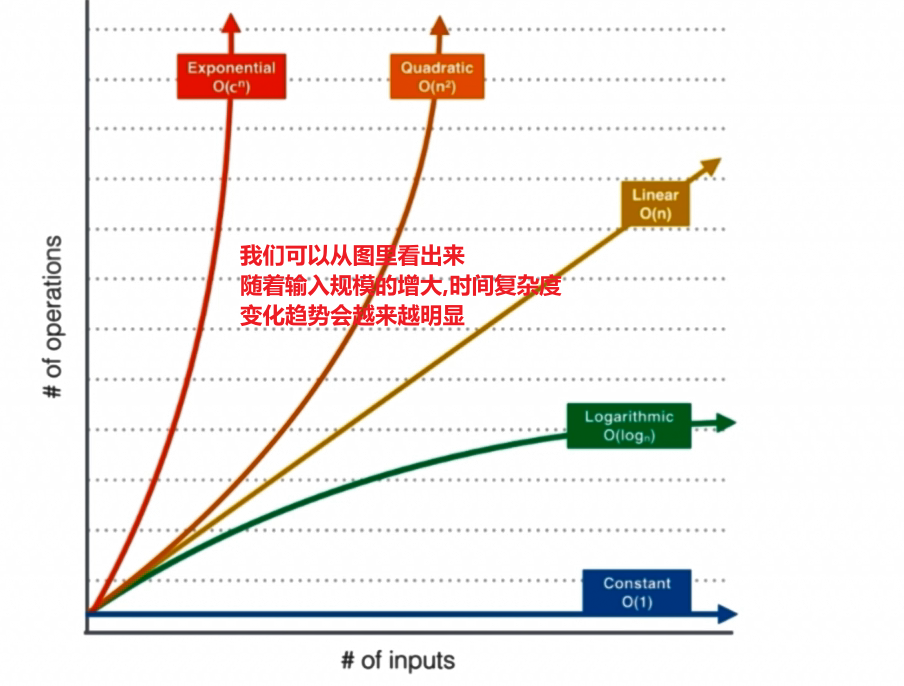
2-1 究竟什么是大O(Big O)
n表示数据规模,f(n)表示n的一个函数
O(f(n))表示运行算法所需要执行的指令数,和f(n)成正比
| 时间复杂度 | Big O |
|---|---|
| 二分查找法 O(logn) | 所需执行指令数:a*logn |
| 寻找数组中的最大/最小值O(n) | 所需执行指令数:b*n |
| 归并排序算法O(nlogn) | 所需执行指令数:c*nlogn |
| 选择排序法O(n^2) | 所需执行指令数:d*n^2 |
-
在学术界,严格地讲,O(f(n))表示算法执行的上界, 归并排序算法的时间复杂度是O(nlogn)的,同时也是O(n^2)
-
在业界,我们就使用O来表示算法执行的最低上界,我们一般不会说归并排序是O(n^2)的
一个问题
有一个字符串数组,将数组中的每一个字符串按照字母序排序;之后再将整个字符串数组按照字典序排序。整个操作的时间复杂度?
我们所考虑的最坏的打算,就是找出字符串数组之中最长字符串长度s,这样就是考虑为最坏的打算
- 假设最长的字符串长度为s;数组中有n个字符串
- 对每个字符串排序:O(slogs)
- 将数组中的每一个字符串按照字母序排序:O(n*slog(s)
- 将整个字符串数组按照字典序排序:O(s*nlog(n)
O(n*slog(s)+O(s*nlog(n)=O(n*s*logs +s*n*logn
=O(n*s*(logs+logn))

2-2 对数据规模有一个概念
对10^5的数据进行选择排序,结果计算机假死?
如果要想在1s之内解决问题:
-
O(n2)的算法可以处理大约10^4级别的数据;
-
O(n)的算法可以处理大约10^8级别的数据;
-
O(nlogn)的算法可以处理大约10^7级别的数据
我们使用下面这种算法进行计算
//
// Created by jiayadong on 2020/9/21.
//
#include <iostream>
#include <cmath>
#include <ctime>
using namespace std;
int main(){
for(int i=0;i<=9;i++)
{
int n = pow(10,i);
clock_t startTime = clock();
int sum = 0;
for(int j=0;j<n;j++)
sum +=j;
clock_t endTime = clock();
cout << "10^" <<i<<":"<< double(endTime - startTime )/CLOCKS_PER_SEC <<" s"<<endl;
}
return 0;
}
空间复杂度
需要注意的是,递归调用是有空间代价的,系统会把递归调用之前的函数状态压入系统栈之中的,
2-3 简单的复杂度分析





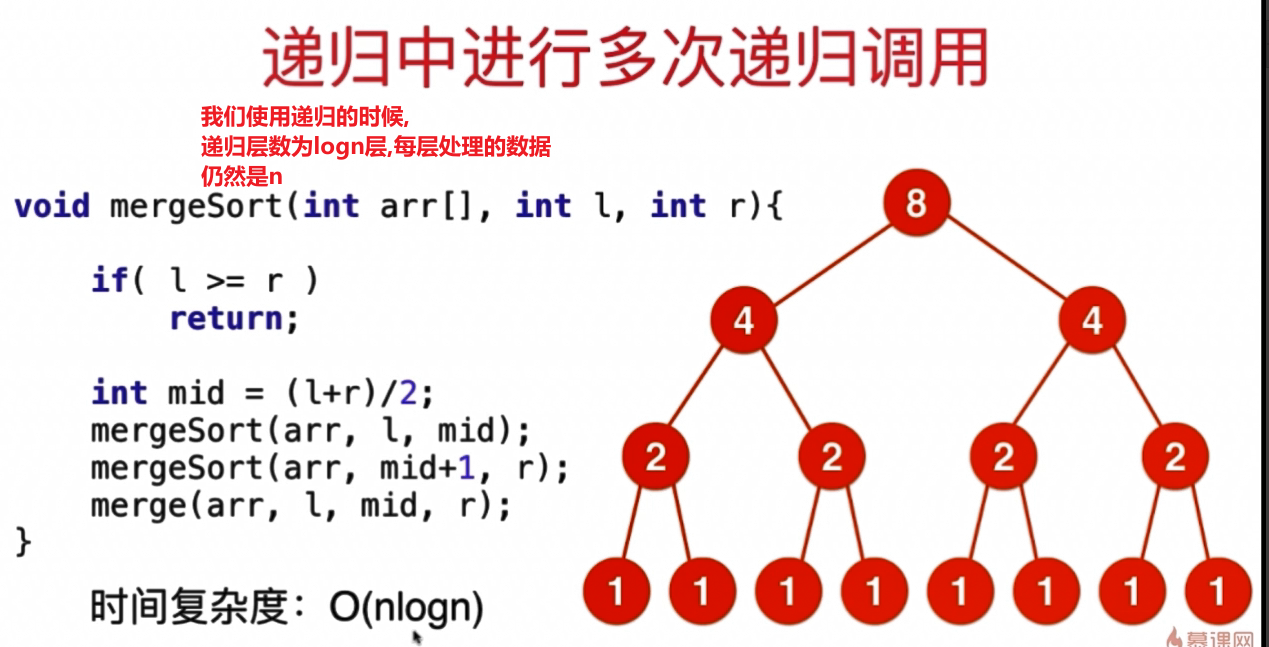
递归函数的时间复杂度
有一个比较重要的公式:主定理,一个递归函数把整个数据分为几份进行递归
2-5 递归算法的复杂度分析
比较典型的例子就是二分法进行测试了
这个问题以后还可以补充一下,就是我们只计算了x的正整数的幂,我们还要计算负数的幂
递归调用的次数和递归调用的次数
当递归式有分叉的时候,我们要考虑递归的深度了
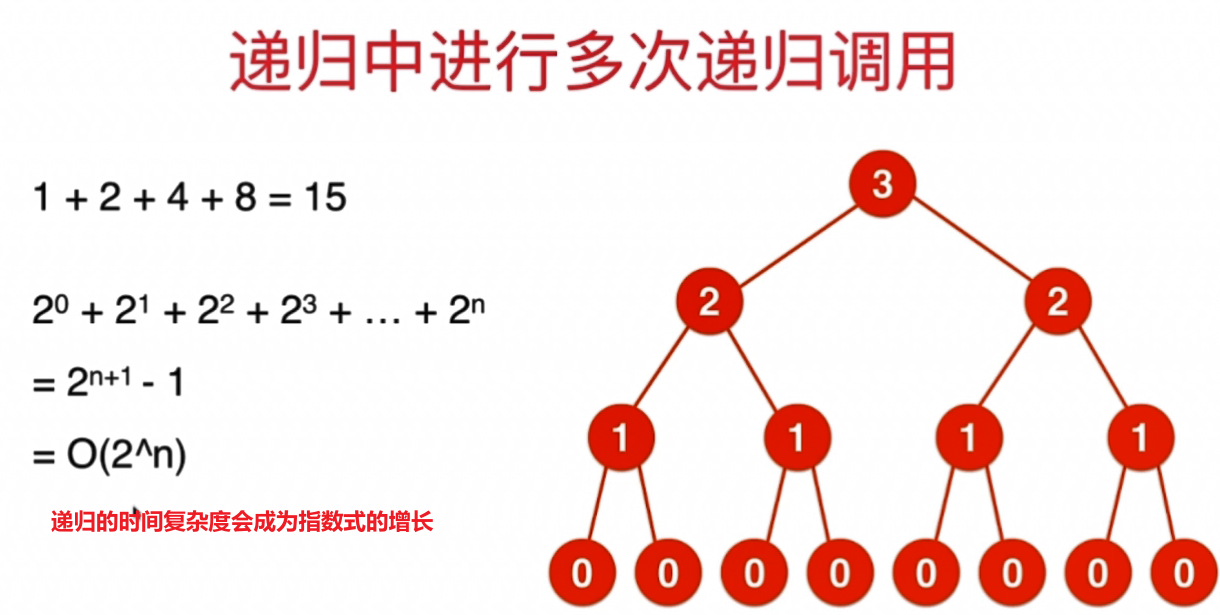
递归的时间复杂度成指数式增长的时候,我们应该注意可以使用剪枝,动态规划,等等方法来进行降低时间复杂度
主定理公式
递归函数的时间复杂度
有一个比较重要的公式:主定理,一个递归函数把整个数据分为几份进行递归,每份的时间复杂度是多少
2-6 均摊时间复杂度分析(Amortized Time Analysis)
vector类
属于均摊时间复杂度一个比较好的例子
均摊时间复杂度,在我看来,是平均时间复杂度的补充。平均时间复杂度只在某些特殊情况下才会用到,而均摊时间复杂度应用的场景比它更加特殊、更加有限。
2-7 避免复杂度的震荡
第3章 数组中的问题其实最常见
面试中的算法问题,有很多并不需要复杂的数据结构支撑。就是用数组,就能考察出很多东西了。其实,经典的排序问题,二分搜索等等问题,就是在数组这种最基础的结构中处理问题的。在这一章中,我们学习常见的数组中处理问题的方法。...
数组在排序中出现的频率很多,
排序
- 选择排序
- 插入排序
- 归并排序
- 快速排序
查找
- 二分查找
数据结构
- 栈
- 队列(优先队列)
- 堆
3-1 从二分查找法看如何写出正确的程序
3-2 改变变量定义,依然可以写出正确的算法
3-3 在LeetCode上解决第一个问题 Move Zeros
283.Move Zeroes 简单题
给定一个数组nums,写出一个函数,将数组所有的0都挪到数组的末尾,而维持其他所有非0元素的相对位置
Given an array nums, write a function to move all 0's to the end of it while maintaining the relative order of the non-zero elements.
Example:
Input: [0,1,0,3,12]
Output: [1,3,12,0,0]
Note:
You must do this in-place without making a copy of the array.
Minimize the total number of operations.
方法一:
思路:我们可以把不为0的元素拿出来,覆盖前面的数字,再把后面的数字覆盖为0
解决步骤:我们申请一个副本数组,先把原数组里面里非0元素拿出来,把副本数组里的值赋值给原数组,继续填充0
//
// Created by jiayadong on 2020/10/16.
//
/*思路一:我们可以把不为0的元素拿出来,覆盖前面的数字,再把后面的数字覆盖为0
*
* */
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
void moveZeroes(vector<int>& nums) {
vector<int> noZeor;
for(int i=0;i<nums.size();i++)
{
if (nums[i]){
noZeor.push_back(nums[i]);
}
}
for(int i=0;i<noZeor.size();i++)
{
nums[i]=noZeor[i];
}
for(int i=noZeor.size();i<nums.size();i++)
{
nums[i] = 0;
}
}
};
int main(){
vector<int> nums{0,1,0,3,12};
Solution one;
one.moveZeroes(nums);
for(int i=0;i<nums.size();i++)
{
cout<<nums[i]<<" ";
}
return 0;
}
*思路一的时间复杂度和空间复杂度都是O(n),对于本题,我们如何才能减少掉额外空间的使用那
方法二:
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int k=0; //nums中,[0...k)的元素均为非0元素
// 遍历第i个位置之后,我们会发现保证[0,,,i)中所有非0元素
// 都按照顺序排列在[0...k)中,
for(int i=0;i<nums.size();i++)
{
if (nums[i]){
nums[k++] = nums[i];
}
}
for(int i=k;i<nums.size();i++)
{
nums[i]=0;
}
}
};
方法三:我们对程序进行优化,能不能不用再一步一步的补0了,可以直接一步到位吗,可以的,我们可以使用交换,将0和后面的整数进行交换,这样零就会被交换到后面了.
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int k=0; //nums中,[0...k)的元素均为非0元素
// 遍历第i个位置之后,我们会发现保证[0,,,i)中所有非0元素
// 都按照顺序排列在[0...k)中,
for(int i=0;i<nums.size();i++)
{
if (nums[i]){
swap(nums[k++],nums[i]);
}
}
}
};
我们还可以处理一些特殊情况,就是假如数组都是非零元素,可能会出现一种情况,就是每个元素都会自己与自己交换
//解决步骤
for(int i=0;i<nums.size();i++)
{
if (nums[i]){
if (i!=k)
swap(nums[k++],nums[i]);
else
k++;
}
}
只需要这么一修改,就可以避免所有都是整数的情况
在这里我们可以思考一下,很多算法不也是为了优化某个问题而产生的吗?
1.快速排序数组(假如传入的数据近乎有序,我们提出了随机选取标定点)2.三路快排(出现大量重复的数据)
27. Remove Element 简单题
给定一个数组和一个数值val,你需要原地移除所以数值等于val的元素,并返回移除后数组的新长度,不用使用额外的数组空间,你必须仅使用O(1)额外额外空间原地修改数组
Given an array nums and a value val, remove all instances of that value in-place and return the new length.Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory. The order of elements can be changed. It doesn't matter what you leave beyond the new length.
我们可以使用一些示例
示例一:
给定 nums = [3,2,2,3], val = 3,
函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。
示例二:
给定 nums = [0,1,2,2,3,0,4,2], val = 2,
函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
注意这五个元素可为任意顺序。
你不需要考虑数组中超出新长度后面的元素。
- 如何定义删除?从数组中去除?还是放在数组末尾?
- 剩余元素的排列是否要保证原有的相对顺序?
- 是否有空间复杂度的要求? O(1)
解题步骤:
和上面使用的方法相同,我们让然是让目标个数覆盖到数组的前面位置,最后再移除掉数组后面无用的位置
具体代码:
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int k=0;
for (int i = 0; i <nums.size() ; ++i) {
if (nums[i]!=val){
nums[k++] =nums[i];
}
}
// 移除尾部数据
nums.erase(nums.begin()+k,nums.end());
return nums.size();
}
};
26. Remove Duplicates from Sorted Array简单题
给出一个排序数组,原地移除重复出现的数字,使每个元素只出现一次,返回数组长度,不用使用额外的空间,你必须使用O(1)额外空间修改数组
Given a sorted array nums, remove the duplicates in-place such that each element appears only once and returns the new length.
Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.
解题步骤:
仍然是使用这个
具体代码:
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.size()==0)return 0;
int k=1;int temp=nums[0];
for(int i=0;i<nums.size();i++)
{
if (nums[i]!=temp){
nums[k++]=nums[i];
temp=nums[i];
}
}
nums.erase(nums.begin()+k,nums.end());
return nums.size();
}
};
遇到的问题:出现了一个问题是
Line 1034: Char 9: runtime error: reference binding to null pointer of type
这个是数组为空的情况吗?
后来我修改了一个判断数组是否为空的条件
if (nums.size()==0)return 0;
80. Remove Duplicates from Sorted Array II
给定一个排序数组,你需要在原地删除重复出现的元素,使得
Given a sorted array nums, remove the duplicates in-place such that duplicates appeared at most twice and return the new length.
Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.
解题步骤:
到这里,我体会到了使用方法的便利,充分了解基础的重要性,我可以根据人家给的观点把问题做出来,可以使用许多方法,我一定要坚持下去
具体代码:
//
// Created by jiayadong on 2020/10/18.
//
#include <iostream>
#include <vector>
using namespace std;
/**
* 思路:有序数组,重复出现,
* 只能出现一次
*/
/**
* 方法一:删除多余的重复项
* 由于输入数组已经排序,所有重复项都显示在旁边,题目要求我们不使用额外空间,在原地修改数组
* 此时最好的方法就是删除多余的重复项,对于数组中出现的每个数字,如出现两个以上,则将多余数字删除
*
*/
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int count =1;
for(int i=1;i<nums.size();i++)
{
//要注意此时的数组是在实时的变化过程之中的,我们应该调整i坐标的值
if (nums[i] == nums[i-1]){
count++;
if (count>2) nums.erase(nums.begin()+i), i--;
} else{
count=1;
}
}
return nums.size();
}
};
int main(){
vector<int> nums{1,1,1,2,2,3,3,3};
Solution one;
one.removeDuplicates(nums);
cout<<"数组长度: "<< nums.size()<<endl;
for (int i = 0; i <nums.size() ; ++i) {
cout<<nums[i]<<" ";
}
return 0;
}
3-5 三路快排partition思路的应用 Sort Color
我们先看一种问题
75. 颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
进阶:
- 一个直观的解决方案是使用计数排序的两趟扫描算法。
- 首先,迭代计算出0、1 和 2 元素的个数,然后按照0、1、2的排序,重写当前数组。
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
在进行做题的过程之中,我们一定要注意,就是以解决问题为目的,只有做出来之后,我们有机会继续改进算法
由于数字个数比较有限,我们可以直接统计三个数的个数,然后直接打印出来
3-6 对撞指针 Two Sum II - Input Array is Sorted
3-7 滑动窗口 Minimum Size Subarray Sum
3-8 在滑动窗口中做记录 Longest Substring Without Repeating Characters






 浙公网安备 33010602011771号
浙公网安备 33010602011771号