区间dp错题

·https://www.luogu.com.cn/problem/P4170
“出师未捷身先死”的思路：既然是l到r能刷成一种，不难想到区间，接着又是最小方案数，可能是区间dp，那肯定有[l][r]，表示【l,r】中变成指定字符串的最小方案量，但是怎么知道上一次把这个区间的字符串都刷成什么了呢？（有这个疑问的原因是既然我要在修改的基础上再次修改，我就得知道上次刷成什么样了，也就是这次我得到的字符串是长什么样子）所以再加一个维度color，表示这个区间里字符串都刷成什么了，然后进行修改，具体代码如下

#include<bits/stdc++.h>
using namespace std;
const int maxn=numeric_limits<int>::max();
string s;
int dp[51][51][26];
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>s;
	int n=s.size();
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<26;j++)
		{
			if(s[i]-'A'==j)
			{
				 continue;
			}
			
			dp[i][i][j]=1;
		}
	}
	for(int i=0;i+1<n;i++)
	{
		for(int j=0;j<26;j++)
		{
			if(s[i]==s[j])
			{
				if(s[i]-'A'!=j)
				dp[i][i+1][j]=1;
			 } 
			 else
			 {
			 	if(s[i]-'A'==j)
				{
					dp[i][i+1][j]=1;
				}
				else if(s[i+1]-'A'==j)
				{
					dp[i][i+1][j]=1;
				}
				else
				dp[i][i][j]=2;
			 }
			
		}
	}
	for(int l=n-3;l>=0;l--)
	{
		for(int r=l+2;r<n;r++)
		{
			for(int color=0;color<26;color++)
			{
				if(s[l]=='A'+color && s[r]=='A'+color)
				dp[l][r][color]=dp[l+1][r-1][color];
				else if(s[l]=='A'+color)
				dp[l][r][color]=dp[l+1][r][color];
				else if(s[r]=='A'+color)
				dp[l][r][color]=dp[l][r-1][color];
				else 
				{
					int start=-1,ans=0;
					for(int i=l;i<=r;i++)
					{
						if(s[i]=='A'+color)
						{
							if(start!=-1)
							{
								dp[l][r][color]+=dp[start][i-1][s[start]-'A']+1;
								start=-1;
							}
							continue;
					    }
						if(start==-1)
						start=i;
					}
					if(start!=-1)
					dp[l][r][color]+=dp[start][r][s[start]-'A']+1;
				}
			}
		}
	}
	cout<<dp[0][n-1][s[0]-'A']+1;
	return 0;
}

这个会WA，只能得40分
正确思路引导：诚如错误思路所言，肯定有[l][r]，表示【l,r】中变成指定字符串的最小方案量，这里抓住题目的特殊点——一个区间全部刷成某个字符，这个有什么用？联系可能性的试法，两端点。那么意味着如果两个端点相同，开头可以带着结尾刷，结尾不用再考虑（也可以是结尾带着开头刷，情况一样），因此就有方程转移，if(s[l]==s[r]) dp[l][r]=dp[l][r-1] （也可以是=dp[l+1][r]）。诶，为什么不能是dp[l+1][r-1]+1呢？从样例一中可以发现AAAAA的时候，会多算，因此不行。ok,现在看当不相等的时候会是什么情况，既然不相等就没得带了，所以个人管个人的，就是枚举分界点就行，这里注意分界点范围[l,r)，不能等于r，额哈哈当时一直检查没检查出来
·https://www.luogu.com.cn/problem/P3205
“出师未捷身先死”的思路：这边想着n<=1000不能暴力，意味着不能枚举，只能抽象化算，最近被这种要抽象化吊打久了条件反射要用dp，首先背包和数位可能性比较小，但是区间好像有点看不出来怎么回事。我一直认为dp讲究的是个可能性尝试，所以我就去找这个规律，我发现，如果是l在最后面，那么它依靠的就是[l+1,r]，r的情况同样适用，想到这里我就和正确思路开始有偏差了：那又不是[l+1,r]的所有情况，万一nums[l]最后组成的数怎么办？最后组成的数又不知道（这里犯了个错误，我在想记录下来最后一个数，但是很显然这会重复我也想到了。后来就没继续思路了。我认为原因是这边思路已经偏具体化，远离了dp设计，而且忘记了dp的每个状态似乎都是同一模式下求解，像分治），而且万一l是开头最先出的数怎么办？（这边似乎忘了r为最后出现的时候应考虑了）哈哈，结果显而易见，思路崩盘
正确思路引导：既然是“出师未捷身先死”的思路，自然有它的可取之处，只要稍微引导一下即可。首先，延续它的可能性落脚点，如果是l最后出现，那么我们考虑在[l+1,r]的范围上最后一个出现的数与l的关系进行讨论即可，然后还有r作为最后出现的情况。那么会发现有两种情况，这时候就要添加另一个维度了，表示是头部最后出现还是尾部最后出现
Leetcode546. 移除盒子
“出师未捷身先死”的思路:这道题首先问的是最大值，想到dp和二分，二分不行于是目光转向dp，观察样例和特殊条件竟然是消除数的题目那应该可以想到区间dp。观察样例，这个似乎只用l,r无法递推，因为有一些相同的是删除了中间的再拼起来的，或者是不拼。那么这时候应该可以想到记录前缀信息。这里我记录的是前面有k个与l-1相同的颜色，与l不相同。然后讨论可能性，这里经过一系列对自己的质疑终究没有讨论出来(⊙o⊙)…。咳咳，先看问题所在，这里我想的是在【l,r】中找一个与l-1相同的数，然后看看后面有没有连着的与之相同的数，进行合并计算答案。这个其实就是正确引导思路，但是后面进行天马行空式杂糅后就出现了
2,2,2……2,2……，2,2 这个前面有多少个2我要记录嘛？不要，因为会杂糅，当我将k和第一个段2进行合并时后面的情况其实都考虑到了，如果加起来的话就考虑不到不要第一个段2的情况
正确思路引导：在上面的思路基础上把那个错误点删除即可
Leetcode1000. 合并石头的最低成本
“出师未捷身先死”的思路:观察发现，每次消耗的都是（k-1）个，所以%一下（k-1）就能判断是否可以分出来。但是最后一个是必须是k，所以公式为（n-1）%（k-1）。这边递推方程出了问题，总的来说是因为设置最大值后相加才会出现问题

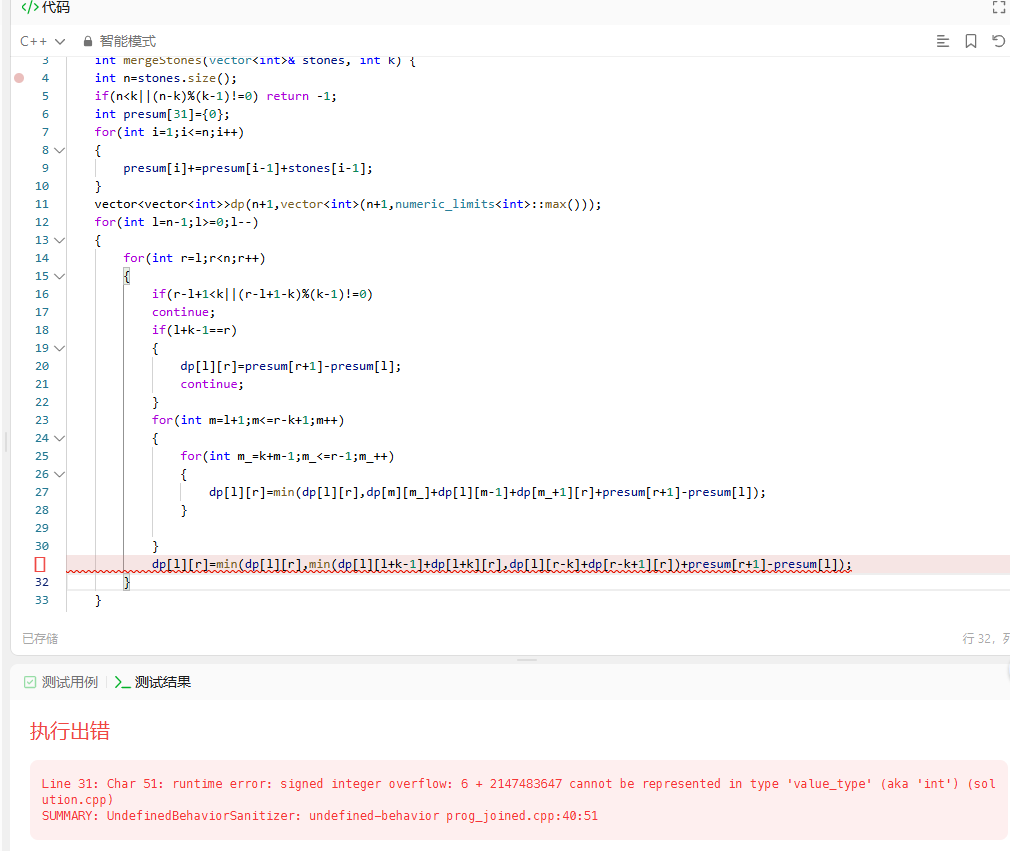
正确思路引导：其实那个思路没有问题，但是需要再进行整理，为了避免加到最大值，dp要全设置为0，所以不能直接给dp[l][r]赋值，而是要设置一个变量ans。ok,现在观察，发现无论可不可以组成一堆，他们最终组成的堆数都是不变的，设置为q。分析可能性，1）可以组成一堆 则要分成 1和k-1堆 这时候枚举1堆的边界点即可，为+=k-1 2）分成p堆（p!=1）则要分成p和p-1堆，同1)
Leetcode730. 统计不同回文子序列
“出师未捷身先死”的思路:两端点的考虑，然后，然后就时间到了（其实是漏看题目信息最后不了了之）
正确思路引导：考虑两个端点
1）s[l]==s[r] 2）s[l]!=s[r]
a.l-1到r-1中没有s[l] (dp[l+1][r-1]<<1)+2 dp[l][r-1]+dp[l+1][r]-dp[l+1][r-1]+mod
b.l-1到r-1中有1个s[l] (dp[l+1][r-1]<<1)+1
c.l-1到r-1中有多个sl-dp[i+1][j-1]+mod
后边用容斥原理或举例子即可 这里的i指的是离l最近的右边的s[l]，j是离r最近的左边的s[l]
综上所述(今天似乎都是出师未捷身先死QAQ）
1.dp是抽象化的，考虑可能性时要抽象->具体->抽象，即题意->用例子规律和题目的特殊性质分心可能性落脚点->转移的时候注意抽象化转移，第一道和第二道都在想记录上一个是什么，但这样不仅累赘而且可能会算重
2.思路错了就退一步，不要完全放弃，也不要拼命死磕，因为你以为的错误思路或许是正解的雏形，你以为的困难或许是南墙
3.dp的每个状态粗略的看来都是同一模式下求解，不要天马行空式地跳出来啊，记住记住，一定要注意状态间算法相同，明确定义，补药杂糅啊！！！2,3写不下去都是这个原因
4.写之前把流程稍微写一下，分析可能性的时候要条理清晰，冷静一点
5.不要看到求最小值就直接整个数组赋无穷大，要分析递推方程的边界和无穷大是否相加，最好整理到草稿纸上不要上来就写即使遇到过相同的题目或题目简单
6.仔细看题
7.不要病急乱投医式或非常兴奋地一头扎近可能性，要跳出来顾全大局式分析可能性