背包问题

From

https://mp.weixin.qq.com/s/_Td9Mh6gT2p_sBNO6Wssdg

动态规划中背包问题，常见有三类：

0-1背包问题

多重背包问题

完全背包问题

（1）0-1背包问题的描述

现在有四种物品，每种物品只有1件，它们的重量与价值如下表。

现在有一个背包，总容量为8。问怎么选取物品，可以使得背包装的物品价值最大？

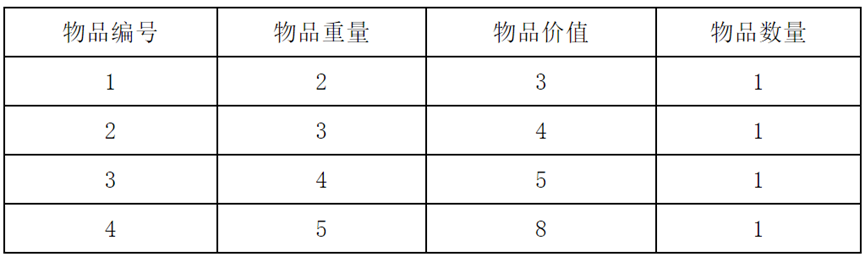
（2）多重背包问题的描述

现在有四种物品，每种物品有若干件，它们的重量与价值如下表。

现在有一个背包，总容量为8。问怎么选取物品，可以使得背包装的物品价值最大？

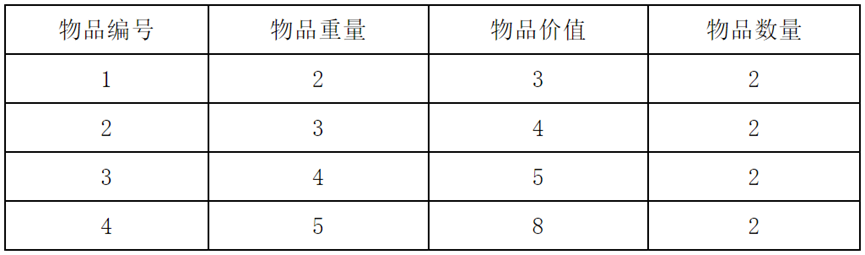
（3）完全背包问题的描述

现在有四种物品，每种物品有无数件，它们的重量与价值如下表。

现在有一个背包，总容量为8。问怎么选取物品，可以使得背包装的物品价值最大？

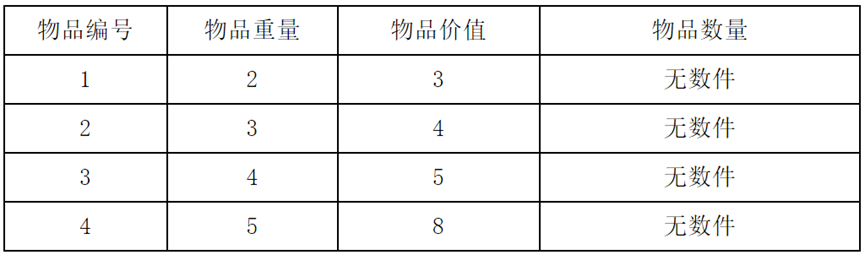
通过以上例子，相信大家大概搞清楚了它们的区别吧。

0-1背包问题就是每种物品只有1件;

多重背包问题就是每种物品有若干件;

完全背包问题就是每种物品有无数件;

一、0-1背包问题

思路：对于每件物品，由于是不可分割的放入，所以，就有两种情况：该物品放入背包与该物品不放入背包；为了将以上问题求解出来，我们需要定义好状态以及状态转移方程。

（1）定义状态

DP[k][w]:表示当背包剩余容量为w，现在有前k件物品可放的情况下，背包所能装物品的最大价值。

DP[4][8]是什么啊？DP[4][8]表示当背包剩余容量为8，现在有前4件物品可放的情况下，背包所能装物品的最大价值。

DP[k][w]怎么求呢，这就是状态转移方程的问题。

（2）状态转移方程

先将状态转移方程写出来吧，就是：

DP[k][w] 等于下列两种情况：

①DP[k][w]=DP[k-1][w]，当w_k>w时

②DP[k][w]=max(DP[k-1][w]，DP[k-1][w-w_i])，当w_k<=w时

解释：

第一种情况，当第k件物品的重量大于背包剩余的容量时，则DP[k][w]=DP[k-1][w];

DP[k][w]表示的是当背包剩余容量为w，现在有前k件物品可放时，背包所能装物品的最大价值。

由于第k件物品太重放不下背包，既然放不下第k件物品，就将其pass（排除）掉呗，相当于考虑放置前k-1件物品的情况，即f[k][w]=f[k-1][w]。

第二种情况，当第k件物品的重量不大于背包剩余的容量时，意味着第k件物品可以放置在背包中，“可以放置”并不意味着一定要放在背包中吧，所以，存在两种情形，第k件物品放在背包中或者第k件物品不放在背包中

这两种情形分别对应两种不同的递推关系式：

DP[k][w]=DP[k-1][w-wi]+v[i];（第k件物品放在背包中的情况，后面的v[i]是指第i件物品的价值，因为放进了背包，所以背包的价值多了v[i]，同理，背包剩余容量就减少了wi）

DP[k][w]=DP[k-1][w];（第k件物品不放在背包中的情况）

所以，第二种情况的结果就是取两种情形的最大值

DP[k][w]=max(DP[k-1][w-wi]+v[i],DP[k-1][w])

综合以上两种情况，DP[k][w]的值就是：

现在，我们要做的就是如何求出DP[4][8]的值，这个值的求解就是通过上面的状态转移方程进行推导，推导的过程就是填写以下表格。

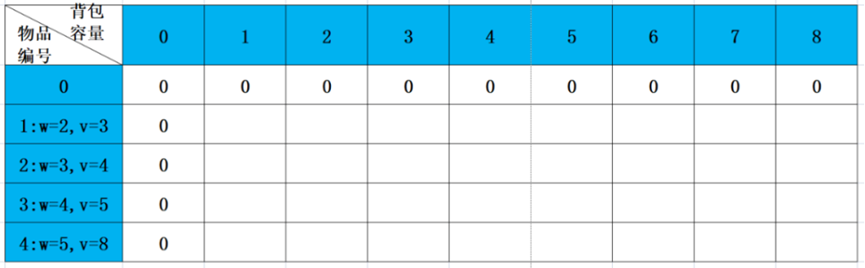
首先，我们对以上表格进行初始化赋值。

第0行的值都为0，DP[0][0]=0,DP[0][1]=0,DP[0][2]=0,DP[0][3]=0,…,DP[0][8]=0，为什么都是0呢，你想呀，因为是考虑前0件物品放进背包时的价值，0件物品的意思是说没有物品可放，既然没有物品可放，当然价值为0；

同理，第0列也都是为0，DP[0][0]=0,DP[1][0]=0,DP[2][0]=0,DP[3][0]=0,DP[4][0]=0，为什么都是0呢，因为背包剩余容量为0，说明背包装不下任何东西了，那么能装的价值当然为0；

以上就是赋初始值，将第0行与第0列都赋值为0，那么其它值该如何推导呢，我们也是根据状态转移方程进行推导，进而可以完成以下表格。

我们举个栗子（哈哈），看看图中红色方格中的数字怎么得到，红色方格代表DP[2][3]，表示的是当背包剩余容量为3，现在有前2件物品可放时，背包所能装的最大价值。因为第2件物品的重量w2=3，此时背包剩余容量为3，说明第2件物品可以放置在背包中，所以，对应于状态转移方程中的第二种情况，DP[2][3]=max(DP[1][0]+4,DP[1][3])=4。

DP[2][3]能这样得到，那么其它方格中的数字，相信大家也一定能推导出来吧。不妨试试推导下DP[4][8]的值吧。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
const int V=10010;
int dp[N][V];
int n,v;//n:物品数量，v:背包实际容量
int w[N];//第n件物品的重量
int c[N];//第n件物品的价值
void knap_01()
{
  for(int i=1;i<=n;i++)
    for(int j=1;j<=v;j++)
    {
      if(w[i]>j)
        dp[i][j]=dp[i-1][j];
      else
        dp[i][j]=max(dp[i-1][j-w[i]]+c[i],dp[i-1][j]);
    }
}
int main()
{
  cin>>n>>v;
  for(int i=1;i<=n;i++)
    cin>>w[i];
  for(int i=1;i<=n;i++)
    cin>>c[i];
  knap_01();
  cout<<dp[n][v];
  return 0;
}

时间复杂度：O(nv)

以上代码我们可以得出答案：DP[4][8]=12，如果我们要输出具体选择的方案，即具体选择了哪些物品呢？我们可以通过DP[4][8]往前进行回溯得到。

怎么回溯呢？再看如下表

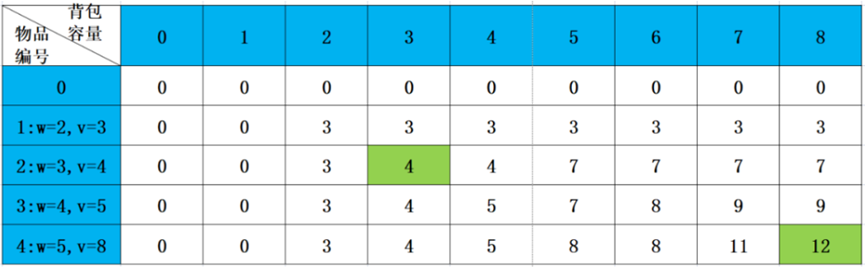
从DP[4][8]进行反向推导，由于DP[3][8]的值等于9，如果背包中没有放入第4件物品，那么DP[4][8]的值一定等于DP[3][8]的值，而两者不相等，说明一定选择了第4件物品。

既然选择了第4件物品，那么DP[4][8]是怎么得到呢，DP[4][8]是通过DP[3][3]+8得到。

DP[3][3]的值与DP[2][3]的值相等，说明没有选择第3件物品。

DP[2][3]的值与DP[1][3]的值不相等，说明选择了第2件物品。

既然选择了第2件物品，那么DP[2][3]是怎么得到呢，DP[2][3]是通过DP[1][0]+4得到，DP[1][0]就是回溯的终点了，无需再进行回溯。

根据以上的过程，本题选择的物品编号分别为2号与4号。

以上过程可以通过递归进行解决，代码如下：

//0-1背包问题
//选择方案的输出
void print(int i,int j)
{
  if(i==0) return;
  if(dp[i][j]==dp[i-1][j])
    print(i-1,j);
  else
  {
    print(i-1,j-w[i]);
    cout<<i<<" ";
  }
}

以上就是0-1背包的思想，总结如下：

1.题目特点

每种物品只有1件，每次要么选择，要么不选择，就有原子性

2.定义状态

DP[k][w]:表示当背包剩余容量为w，现在有前k件物品可放的情况下，背包所能装物品的最大价值。

3.状态转移方程

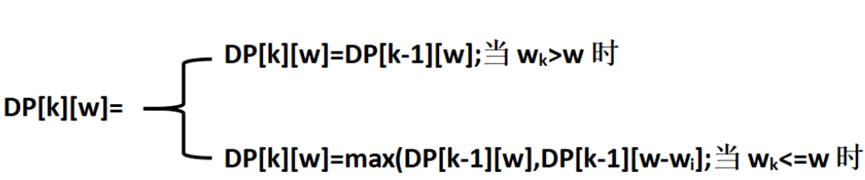
4.时间复杂度：O(nv)

5.方案的输出：使用回溯，运用递归，轻松输出

二维费用01背包问题：

背包的限制条件有两个，此时我们直接加上一重循环即可。注意二维限制可以加在任意类型的背包问题上。

例题：

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。

每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。输出最大价值。

输入格式：

第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

输出格式：

输出一个整数，表示最大价值。

思路：

该题为二维费用的01背包。f[i][j][k]表示前i个物品，背包体积为j，承重为k的时候的最大价值。在01背包基础上加上一重循环即可。由于n*3的空间太大，所以我们直接使用优化后的01背包。

数据范围

0< N≤ 1000

0< V，M ≤100

0< vi，mi ≤ 100

0< wi ≤ 1000

输入样例

4 5 6

1 2 3

2 4 4

3 4 5

4 5 6

输出样例：

N：物品件数 ,V：背包的容量,M：背包能承受的最大重量

Vi：第 i 件物品的体积 ,mi：第 i 件物品的重量 ,wi：第 i 件物品的价值

这道题目属于经典的二维费用的零一背包问题，是一维零一背包的扩展，一维的时候只有一个背包的体积，二维的时候多了一个背包最大重量的限制，一维的时候使用一维数组来表示对应的状态，其中dp[i]表示体积为i的背包的最大价值，类似于一维的表示方式在二维的时候可以使用二维的数组或者列表来表示对应的状态，其中dp[i][j]表示体积为i重量为j的情况下背包的最大价值，这个过程类似于一维零一背包问题，因为多一个重量的限制所以我们需要使用三重循环进行状态的计算。第一重循环枚举当前的n个物品，第二重循环枚举体积，第三重循环枚举重量。因为是零一背包问题所以我们在枚举的时候需要逆序枚举体积和重量这样才可以保证物品是选择一次的。

#include<iostream>
using namespace std;
 int f[1010][1010];
int N, V, M; 
int main() {
    cin >> N >> V >> M; 
    int v, m, w;
    for (int i = 0; i < N; i++) {
        cin >> v >> m >> w;
        for (int j = V; j >= v; j--)
            for (int k = M; k >= m; k--)
                f[j][k] = max(f[j][k], f[j - v][k - m] + w);
    } 
    cout << f[V][M]; 
    return 0; 
}

例题：

样例数据分析:

考察知识:

动态规划,二维费用的背包问题,在01背包问题的基础上增加一个费用维度

状态转移方程:

yh[i][j][k]=max(yh[i-1][j][k],yh[i-1][j-w[i]][k-v[i]]+n[i])

总体思路：

1.先从后往前推，得到最大让利金额，并形成具体方案（仿照最短路问题，从后往前）

2.再从前往后推，得到具体方案的字典序

#include<iostream>
#include<algorithm>
#include<fstream>
using namespace std;
const int N=110;
int w[N],v[N],p[N];
int f[N][N][N];
int main()
{
    //freopen("shopping.in","r",stdin);
    int W,V,n;
    cin>>W>>V>>n;
    for(int i=1;i<=n;i++) cin>>w[i]>>v[i]>>p[i];
    //求最短路，从后往前推 
    for(int i=n;i>=1;i--){
        for(int j=0;j<=W;j++)
            for(int k=0;k<=V;k++){
                f[i][j][k]=f[i+1][j][k];
                if(j>=w[i] && k>=v[i])
                    f[i][j][k]=max(f[i][j][k],f[i+1][j-w[i]][k-v[i]]+p[i]);
                }
    }
    cout<<f[1][W][V]<<endl;
    //字典序向后推 
    int j=W,k=V;
    for(int i=1;i<=n;i++)
        if(j>=w[i] && k>=v[i] && f[i][j][k]==f[i+1][j-w[i]][k-v[i]]+p[i]){
            cout<<i<<' ';
            j-=w[i],k-=v[i];
        }
    puts("");
    return 0;
}

posted @ 2023-03-08 09:29 jhtchina 阅读(129) 评论(0) 收藏举报

厚道善良守信宽容诚实谦虚正直执着

背包问题

公告

厚道 善良 守信 宽容 诚实 谦虚 正直 执着

背包问题

公告

厚道善良守信宽容诚实谦虚正直执着