[SOM] Cluster with Self-Organizing Map Neural Network

初步认知

SOM(自组织映射神经网络)——理论篇

Ref: https://github.com/tcosmo/tcosmo.github.io/tree/master/assets/soms【唯一好文，楼主好人】

一、基本特点

竞争学习(competitive learning)策略,依靠神经元之间互相竞争逐步优化网络。

近邻关系函数(neighborhood function)来维持输入空间的拓扑结构。

在不知道类别的情况下，对数据进行聚类；可以识别针对某问题具有内在关联的特征。

特点归纳：

• 神经网络，竞争学习策略
• 无监督学习，不需要额外标签
• 非常适合高维数据的可视化，能够维持输入空间的拓扑结构
• 具有很高的泛化能力，它甚至能识别之前从没遇过的输入样本

 

二、训练前

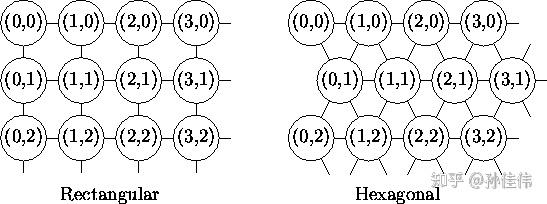
二维平面有2种平面结构：

• • Rectangular
  • Hexagonal

 

一条经验公式：

竞争层最少节点数量 = 

N：训练样本的个数

 

三、训练计算过程

第一步：与其他神经网络相同，需要将Weighs初始化为很小的随机数

第二步：随机取一个 输入样本X_i

第三步：

1. 1. 遍历竞争层中每一个节点：计算 X_i与节点之间的相似度 (通常使用欧式距离)
   2. 选取距离最小的节点作为 优胜节点 (winner node)，有的时也叫 BMU (best matching unit)

第四步：根据 邻域半径σ(sigma) 确定 优胜邻域 将包含的节点；并通过 neighborhood function 计算它们各自更新的幅度 (基本思想是：越靠近优胜节点，更新幅度越大；越远离优胜节点，更新幅度越小)

第五步：更新优胜邻域内节点的Weight：

W_v(s+1) = W_v(s) + θ(u,v,s) · α(s) · ( D(t) - W_v(s) )

θ(u,v,s)是对更新的约束，基于离BMU的距离 即neighborhood function的返回值
W_v(s)是节点v当前的Wight

第六步：完成一轮迭代(迭代次数+1)，返回第二步，直到满足设定的迭代次数

 

bubble函数很好地去近似估计高斯

 

 

 

使用经验

一、不错的代码

SOM(自组织映射神经网络)——案例篇

在用经典的Iris数据集来展示SOM的效果与优点。

代码：https://github.com/JustGlowing/minisom 【example文件夹里啥都有】

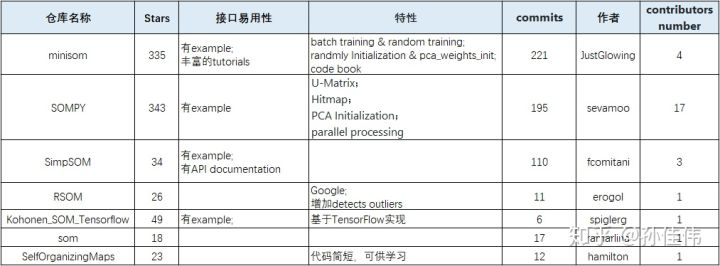
主要还是一些关键概念的实现。

 

二、竞争学习策略

Ref: 机器学习(五)： 神经网络(四)：SOM网络和级联相关网络【没说什么】

Ref: 【公开课】机器学习及其Matlab实现【13集】第五课：竞争神经网络与SOM神经网络【也没说什么】

 

Ref: Machine Intelligence - Lecture 7 (Clustering, k-means, SOM) - SYDE 522 – Machine Intelligence (Winter 2019, University of Waterloo)

SOM模型本质上是一种只有输入层--隐藏层的神经网络。隐藏层中的一个节点代表一个需要聚成的类。

因为SOM自组织映射应用竞争学习，而不是纠错学习（例如BP神经网络）。并且SOM自组织映射使用邻域功能来保持输入的拓扑性质。

SOM的三个步骤：

(1) Competition

(2) Collaboration

(3) Weight update

 

三、细节分析

 

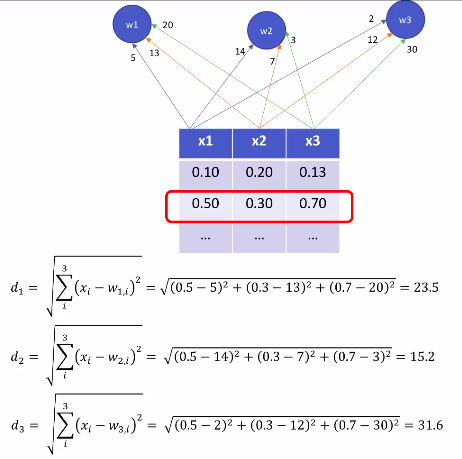
可见，i = 2时，距离最小，是竞争的胜利者！

 

然后开始更新"一部分"权重。

 

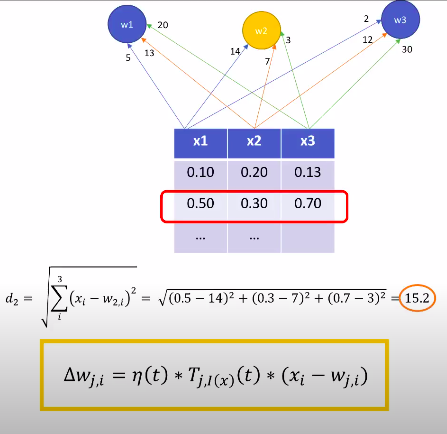
学习率 and 拓扑邻居

 

 

Ref: Kohenen self organizing maps(KSOFM) with algorithm and solved example【手推公式，有点用处】

Ref: Self-Organizing Maps Intuition Video【细节演示】