后训练量化——Data free quantization

(本文首发于公众号，没事来逛逛)

前面介绍了一些后训练量化的基本方法，从这篇文章开始我们来学习一些高阶操作。

首先登场的是高通提出的一篇论文：Data-Free Quantization Through Weight Equalization and Bias Correction。之所以介绍它是因为笔者在使用高通的模型量化工具 Snapdragon Neural Processing Engine (SNPE) 时感觉效果奇好，而 weight qualization 和 bias correction 就是该工具中提供的常用算法，应该说是比较成熟的量化技术了，况且算法本身也有很多巧妙之处，值得学习。

三个关键点

这篇论文发表于 2019 年的 ICCV 会议，但在此之前高通就已经将它落地到自己的工具中了，算是有一定知名度的论文。学习这篇论文只要把握住三个点就可以：Data-Free、Weight Equalization、Bias Correction (好的题目可以把握住读者的心)。

Data-Free Quantization

第一点 Data-Free，也是最不重要的一点，我觉得是高通搞出来的一点噱头。

高通在论文提出了模型量化算法的四重境界。

第一重，不需要数据，不需要重训练，不 care 模型结构，看一眼你的网络就可以自动帮你量化好。这一重即论文提到的 Data-Free。但这种一般只对 weight 量化起作用。高通说它的方法是 Data-Free 的，意思就是说它对 weight 的量化方法非常鲁棒，数据都不用就给你量化好了，效果还很好。当然对 feature 的量化还是得老老实实用数据来统计数值范围的。

第二重，需要数据，但不需要重训练，也不 care 模型结构。这种是目前大部分后训练量化追求的，用少量的数据达到最好的量化效果。这也是对 feature 进行量化的最低要求。但有些论文为了对 weight 做更好的量化，也会需要一点数据来辅助优化 (高通说：弟弟们，我不用，我 Data-Free)。

第三重，需要数据，也需要重训练，但不 care 模型结构。这种就是量化训练追求的最高境界了。

第四重，需要数据，也需要重训练，模型结构还不能乱来。这种指的是最 navie 的量化训练，一遇到特殊的结构或者压缩很厉害的模型就 gg 的那种。

Weight Equalization

weight equalization 是论文的关键点之一，这在另一篇论文 Same, Same But Different\(^1\) 中也有所提及。

weight equalization，顾名思义，就是对 weight 进行均衡化操作。为什么要有这个操作呢？因为高通研究人员在剖析 MobileNetV2 的时候发现，这个网络用 per-layer 量化精度下降极其严重，只有用上 per-channel 的时候才能挽救一下。具体实验数据出自 Google 的白皮书。我特意去翻了一下，发现还真是：

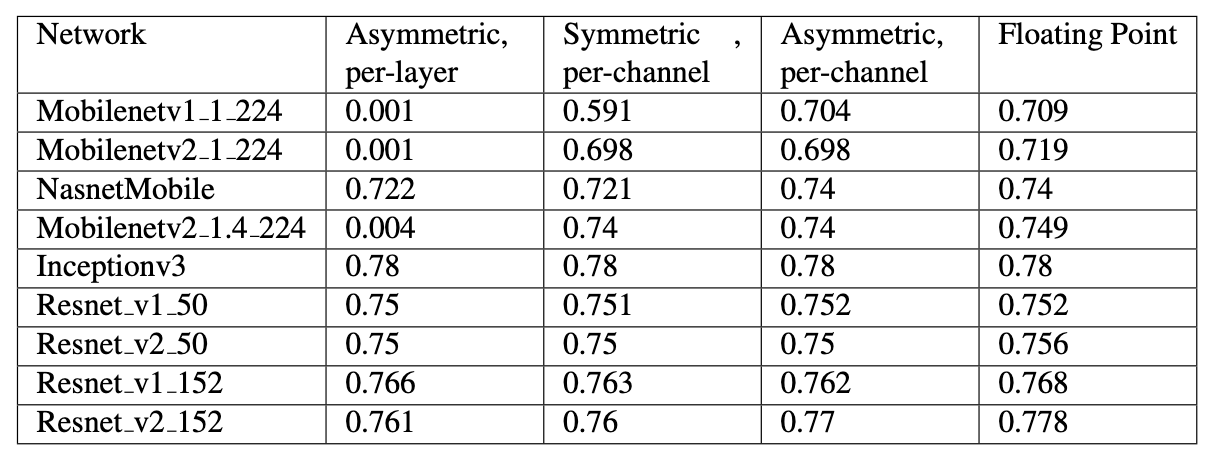
Mobilenet 类的网络在 per-layer 量化下，精度直接掉到 0.001 了，而同样作为小网络的 Nasnet 下降很小 (per-layer 精度一般是比 per-channel 低一些，但这么严重的精度下降，我怀疑是不是 Google 的程序员跑错代码了)。

为什么会有这种情况呢？原因在于 MobileNetV2 中用了大量的可分离卷积 (depthwise conv)，这个卷积的特殊之处是每个 output channel 都只由一个 conv kernel 计算得到，换句话说，不同 channel 之间的数值是相互独立的。研究人员调查了某一层可分离卷积的 weight 数值，发现不同的卷积核，其数值分布相差非常大：

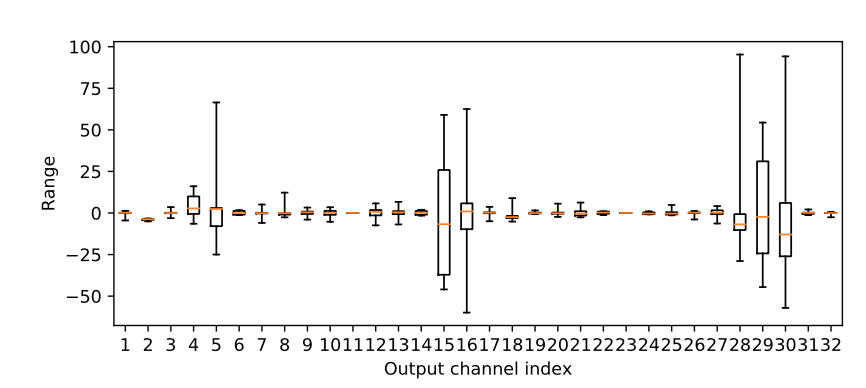
纵坐标是数值分布，横坐标表示不同的卷积核。你会发现，有些 weight 的数值分布在 0 附近，有些数值范围就非常大。在这种情况下，如果使用 per-layer 量化，那这些大范围的 weight 就会主导整体的数值分布，导致那些数值分布很小的 weight 在量化的时候直接压缩没了。这也是为什么 per-channel 对可分离卷积效果更好的原因。

而 weight equalization 要做的事情，就是在使用 per-layer 量化的情况下，使用一些方法使得不同卷积核之间的数值分布能够均衡一些，让大家的数值分布都尽量接近，这样就可以用 per-layer 量化实现 per-channel 的精度 (毕竟 per-channel 实现上会比 per-layer 复杂一些)。

高通说他们实现这一步并不需要额外的数据，可以优雅地在 Data-Free 的情况下实现，这也是他们给论文起名 Data-Free 的缘由。具体的算法我们后面再说。

Bias Correction

除了 weight 的问题之外，研究人员发现，模型量化的时候总是会产生一种误差，这种误差对数值分布的形态影响不大，但却会使整个数值分布发生偏移 (biased)。

假设有 \(N\) 个样本，那么对于 feature map 上面的每一个数值，我们可以用下面这种方式计算偏移误差 (biased error)：

\[E[\widetilde{y_j}-y_j]\approx\frac{1}{N}(\sum_n(\widetilde{W}x_n)_j-(Wx_n)_j) \tag{1} \]

其中，\(\widetilde{W}\) 是量化后再反量化的 weight (即带了量化误差)，\(W\) 是原先的 weight，\(x_n\) 是输入，对应的 \(\widetilde{y_j}\) 是量化后的输出，\(y_j\) 是原输出。

用这个公式可以算出引入量化误差后的 feature map 上每个点和原先的相差了多少，统计一下这些误差，就得到下面这张图：

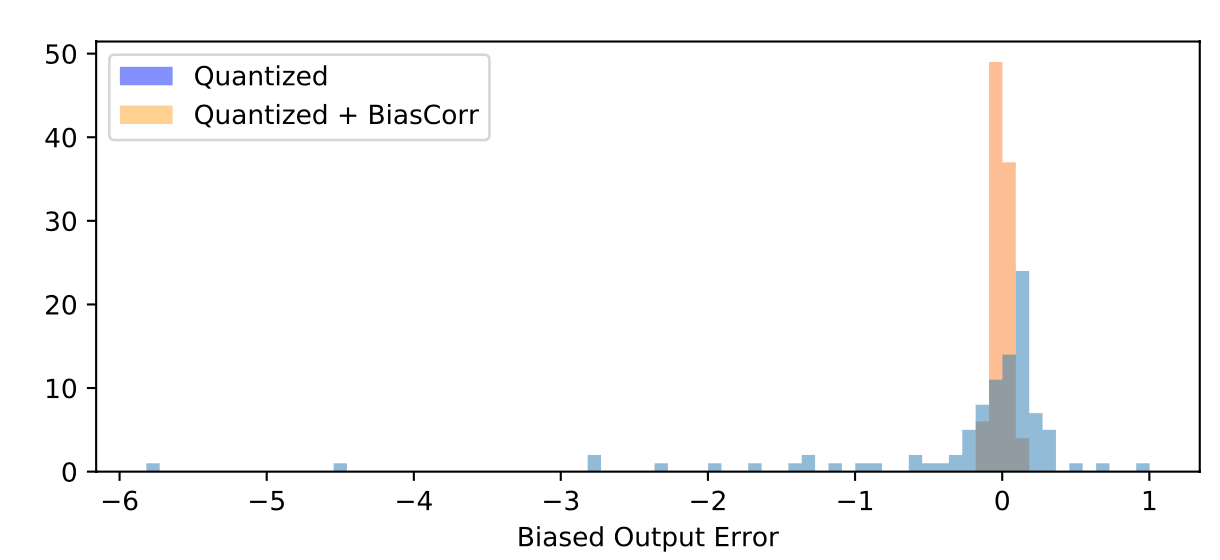
这里面蓝色的柱状图就统计了量化后的误差分布，看得出，有不少 feature 的误差已经超过了 1，而理想状态下，我们是希望量化后的误差能集中到 0 附近，越接近 0 越好，就像橙色直方图那样。

其实，这种 biased error 不仅仅只有量化的时候会出现，在做模型压缩的时候也会遇到。做过画质类任务模型剪枝的同学可能有这种体验，就是当你把一个大模型里面某些卷积的通道数砍掉时，会发现模型的输出结果出现一种整体上的色彩变化。比如，我在一个图像去噪的实验中用了剪枝后，出现下面这种现象：

模型剪枝后，你会发现模型的输出结果和原来相比，好像整体的颜色上多了一个偏移 (biased)，但图像里面的物体基本还能辨识 (数值分布的形态没有发生变化)。

我自己画了幅简图描述这种现象：

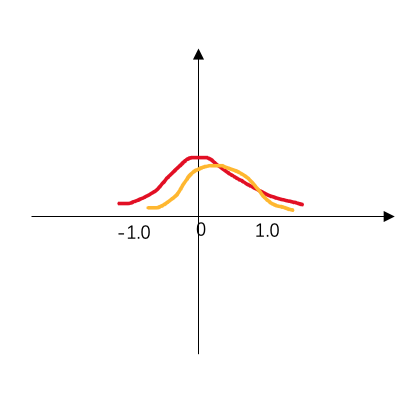
其中红色的分布是原模型的分布，而橙色分布就是剪枝后带了 biased error 的分布，它的形状大体上和红色分布类似，但整体向右发生了一点偏移，从而导致整个画面的色彩发生了变化。一般来说，经过 finetune 后，这种现象可以慢慢得到缓解。

以上是我对 biased error 的一些理解。

研究人员发现，用上 weight equalization 后，这种 biased error 会更加地突出。而 Bias Correction 就是为了解决该问题提出的。

具体方法

Weight Equalization

要实现 Weight Equalization，一个很直接的想法就是对卷积核的每个 kernel (或者是全连接层的每个权重通道) 都乘上一个缩放系数，对数值范围大的 kernel 进行缩小，范围小的则扩大。

Positive scaling equivariance (伸缩等价)

不过，乘上放缩系数的同时不能影响网络的输出。为了保证计算上的等效性，论文利用了卷积层 (包括全连接层) 和 ReLU 这类激活函数的伸缩等价性 (Positive scaling equivariance)。

卷积层和全连接层，本质上都是加权求和 (线性映射)，因此都满足下式：

\[f(sx)=sf(x) \tag{2} \]

(注意这个式子的 \(s\) 必须是正数)

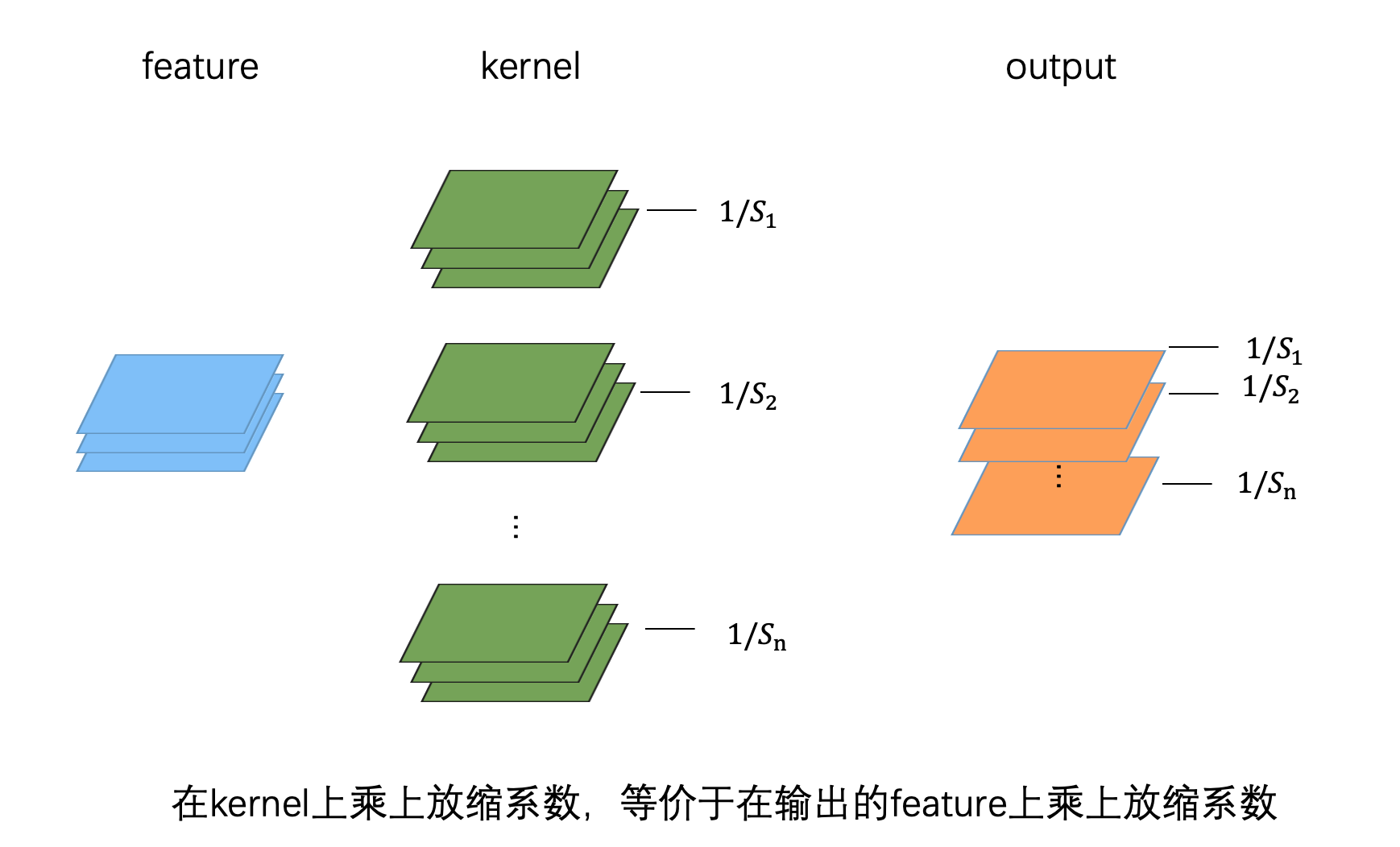
对于卷积来说，在卷积核上乘以放缩系数，等效于在输出上乘以同样的放缩系数。全连接层同理。(简单起见，上图中的 bias 被省略了)

如果卷积后跟着一个类 ReLU 的激活函数 (ReLU、LeakyReLU 等)，那么 (2) 式也是成立的，因为 ReLU 这类激活函数本质上也是分段线性的。

\[ReLU(sx)=sReLU(x) \tag{3} \]

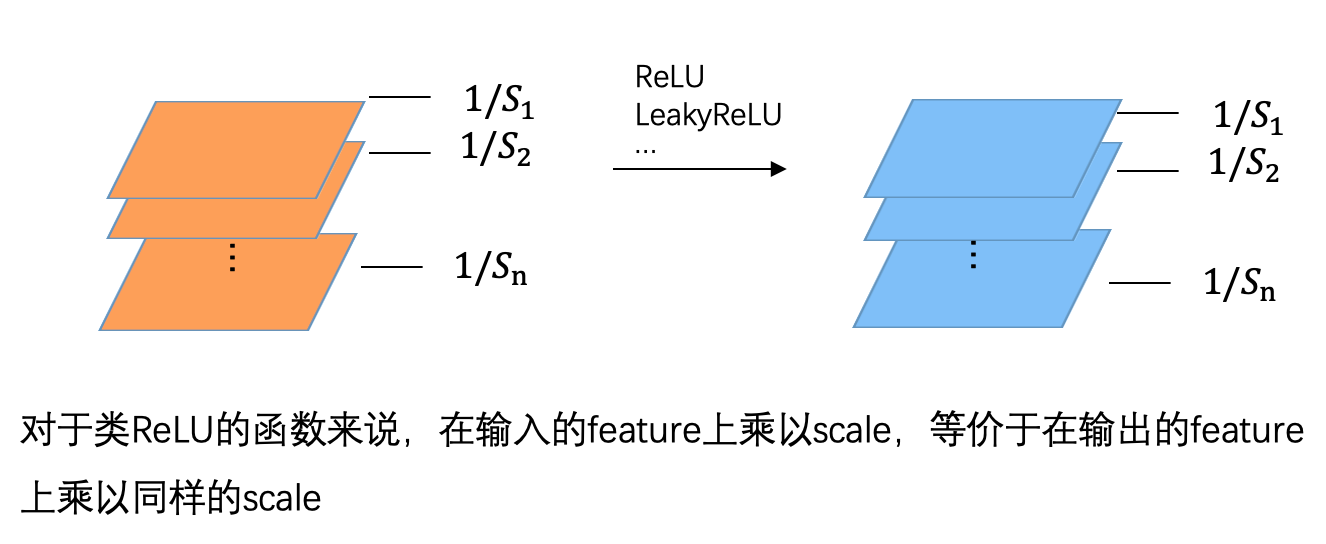
其实不只是 ReLU，任何分段线性的函数，都满足 Positive scaling equivariance。不过由于我们大部分时候使用的都是类 ReLU 的函数，所以这里就不再延伸了。

有了以上这些性质后，我们就可以在下一个卷积核上，乘以一个逆放缩系数，从而抵消第一个卷积核放缩的影响，实现计算上的等效性。

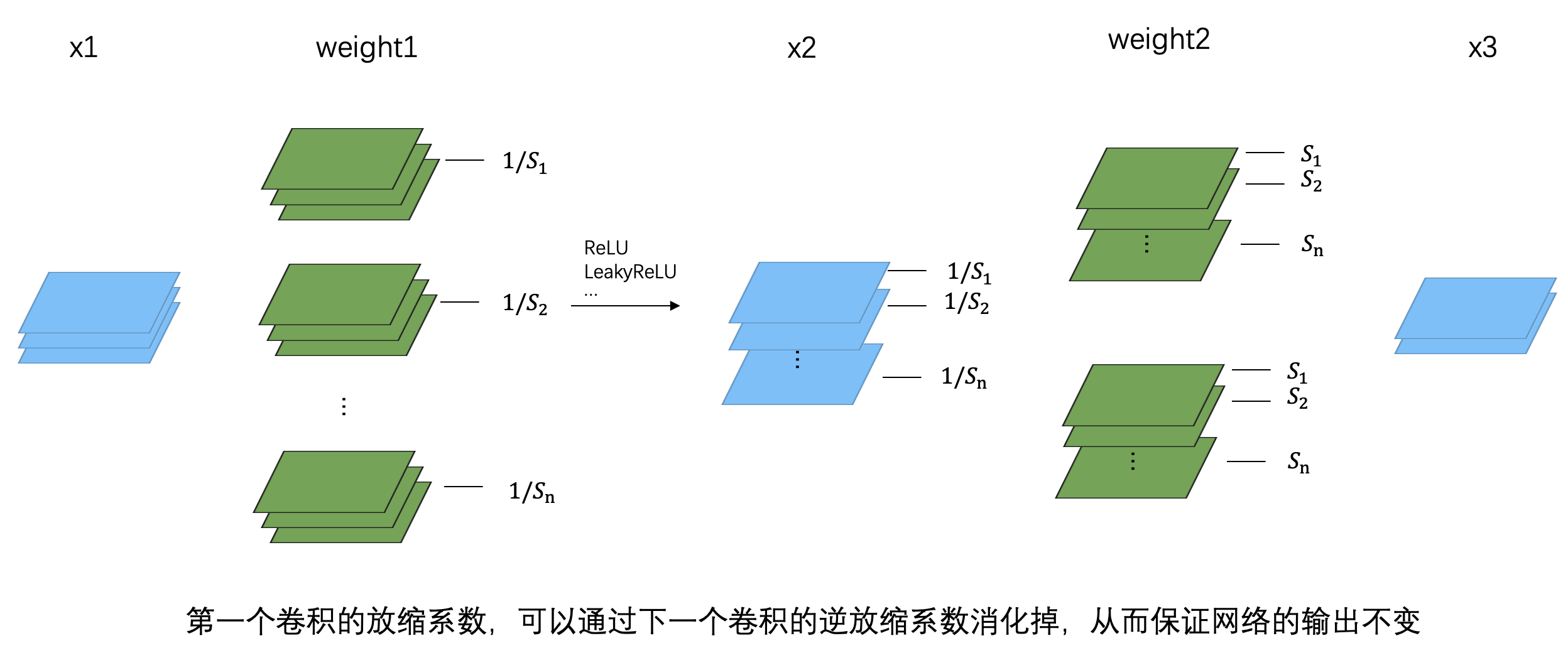
这一切成立的前提都在于 conv 和类 ReLU 函数满足公式 (2)，从而可以把缩放系数等价地作用到下一层输入上，并进一步被下一层卷积的逆缩放系数吸收掉。需要注意的是，第一个卷积的缩放系数是乘在每个 kernel 上，而第二个卷积的逆缩放系数则是乘在每个 kernel 的 channel 上的。

这个过程总结一下就得到了论文中的公式：

\[\begin{align} y&=f(W^{(2)}f(W^{(1)}x+b^{(1)})+b^{(2)}) \tag{4} \\ &=f(W^{(2)}S\hat{f}(S^{-1}W^{(1)}x+S^{-1}b^{(1)}) +b^{(2)}) \tag{5} \\ &=f(\hat{W}^{(2)}\hat{f}(\hat{W}^{(1)}x+\hat{b}^{(1)}) +b^{(2)}) \tag{6} \end{align} \]

如何找到放缩系数S

下一步就是如何找出合适的放缩系数 \(S\)。

回到开头，我们在 weight 上乘以 \(S\) 的目的是为了让不同 kernel 之间的数值尽可能相同，从而达到均衡化。为此，论文定义了一个指标来描述这种均衡化的程度 (称为均衡化系数)：

\[p_i^{(1)}=\frac{r_i^{(1)}}{R^{(1)}} \tag{7} \]

这里面，\(r_i^{(1)}\)表示第一个卷积核的第 i 个 kernel 的数值范围，\(R^{(1)}\) 则表示第一个卷积核整体的数值范围。理想情况下，当然是每个 kernel 的数值范围都近似整个卷积核的数值范围 (即 \(p_i^{(1)}\) 的数值越大)，均衡化的程度越好。

不过，由于我们把缩放的代价转移到了下一个卷积核上了，因此，我们同时要让这种代价越小越好。所以，对于下一个卷积核来说，它那些被缩放的权重也应该尽可能地均衡。

需要注意的是，在计算下一个卷积核的均衡化系数时，不能像第一个卷积核一样每个 kernel 单独计算，而应该把相同缩放系数的通道重新排列后，再按照前者的方式计算。(只是求解缩放系数的时候需要这么处理，正常卷积运算还是按照原来的卷积核来算)

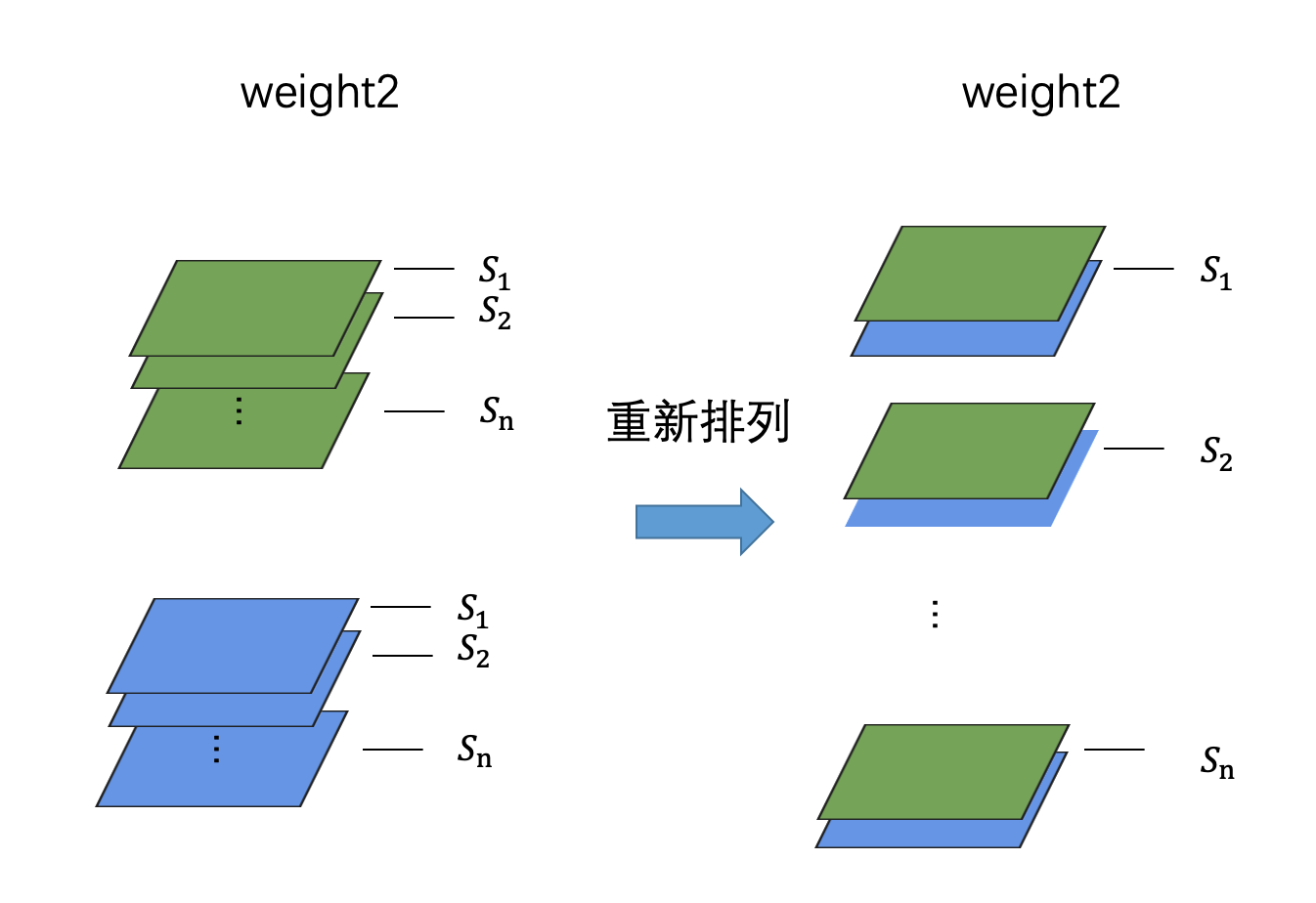
这种处理方法在数学优化以及代码实现上都能带来极大的方便。卷积核重新排列后，第二个卷积核的 kernel 数就和第一个相同了。

由此，论文给出了最终的优化函数：

\[\underset{S}{\operatorname{max}} \sum_i p_i^{(1)}p_i^{(2)} \tag{8} \]

这个式子翻译成人话就是，第一个卷积核和第二个卷积核 (重排后)，它们每个 kernel 的均衡化系数要尽可能大，而让所有 kernel 的系数之和最大的那个缩放系数 \(S\)，就是我们想要的。

论文只针对对称量化求解这个函数，非对称量化结果也是一样的。具体求解过程在论文附录里面已经给出了，感兴趣的同学可以自行参考。实在看不懂的话，也不用过分纠结，毕竟求解一个数学问题是数学家要做的事，作为工程师，我们要做的是在了解原理的情况下把想法实现。

这里直接给出最终的答案：

\[s_i=\frac{1}{r_i^{(1)}}\sqrt{r_i^{(1)}r_i^{(2)}} \tag{9} \]

这就是每个 kernel 最优的放缩系数了。

至此，两个卷积核的 equalization 算法可以通过下面的代码实现：

def equalize(weight1, bias1, weight2):
    # 重排列
    weight2 = weight2.permute(1, 0, 2, 3)
    out_channel = weight1.shape[0]
    for i in range(out_channel):
	r1 = compute_range(weight1, i)  # 计算kernel数值范围
	r2 = compute_range(weight2, i)
        s =  r1 / sqrt(r1 * r2)
	weight1[i] = weight1[i] * (1. / s)
	weight2[i] = weight2[i] * s
        bias1[i] = bias1[i] * (1. / s)
    # 调整回之前的数据排布
    weight2 = weight2.permute(1, 0, 2, 3)
    return weight1, bias1, weight2

在实际操作中，我们会以两个相邻的 conv 为一组 (比如 conv1、conv2 为一组，conv2、conv3 为一组)，按顺序逐个计算每一组的缩放系数，逐层逐层地做 weight equalize 直到结尾。

另外，我们上面的讨论都忽略了卷积里面 bias 的影响。论文提到，如果 \(s < 1\)，那么第一个卷积的 bias 相当于被放大了，这种情况下会导致 activation 里面某些 channel 的数值也被放大 (类似于形成某种 biases)，使得 activation 的 channel 之间也变得不够均衡化。因此，论文提出一种方法，可以把这个 biases 吸收掉 (Absorbing high biases)。

不过，论文对这种方法做了一个很严格的假设，作者假设 activation 会经过 batchnorm 层，使得数值分布接近高斯分布。但在实际情况中，这个假设过于严格，并非每个卷积层之后都会跟上一个 BN 层。因此，我觉得这个方法局限性比较大，不够通用，这里就不过多介绍了。

Bias Correction

前面提到，量化可能会破坏模型的数值分布，使得输出结果产生一个偏移 (biased)，因此需要对这个偏移做一点矫正。

假设原始全精度模型的权重是 \(W\)，而带了量化误差的权重是 \(\hat{W}\) (这里的权重是将 \(W\) 进行量化后再反量化得到的，熟悉量化训练的同学应该不陌生)。由于 bias 量化引起的误差一般较小，一般不考虑，因此，可以大致估算出量化导致的误差偏移为：

\[E[\epsilon x]=E[Wx]-E[\hat{W}x]=E[(W-\hat{W})x] \tag{10} \]

\(E[x]\) 表示从几个样本上计算得到的均值，又称期望，而 \(\epsilon=W-\hat{W}\)。

算出误差 \(E[\epsilon x]\) 后，我们可以从卷积或者全连接层的 bias 里面减掉这个误差，这样一来，就通过 bias 把这个偏移抵消掉，因此把这种方法称为 bias correction。

在手头上有数据集的情况下，我们可以从数据集里面拿出 \(N\) 个样本，然后，分别跑一遍全精度模型和量化模型 (这里是量化后再反量化的权重，同时做了 weight equalization)，针对每一层输出，按照公式 (10) 计算出偏移后，再从对应层的 bias 上减掉这个偏移即可。需要注意的是，后面层在计算误差时，要等前面层已经做了 bias correction 后再进行，防止前面层已经矫正的偏移量传导到后面的层。

如果手头上没有数据，而网络里面刚好使用了 BatchNorm，那就又到了论文秀 Data-Free 的时间了。

根据期望的性质 \(E[\epsilon x]=\epsilon E[x]\)，由于 \(\epsilon\) 是可以根据权重计算的，因此只要知道 \(E[x]\)，即输入的期望即可。那该如何在没有输入数据的情况下，得到输入的期望呢？论文假定，对于某一层 Conv 层，它的前一层跟着一个 BN 层和一个类 ReLU 的激活函数：

我们只要算出 ReLU 的输出的均值，那就相当于我们得到了所要求的 Conv 的输入均值 \(E[x]\)。这里起关键作用的是 BN，我们知道，BN 里面有两个参数：\(\gamma\) 和 \(\beta\)，它们表示 scale 和 shift，但同时它们还包含另一层物理意义，即均值和方差。换句话说，上面这幅图里面，\(x^{pre}\) 的均值就是 \(\gamma\)。

所以，如果没有中间的 ReLU 函数的话，我们就可以直接用 BN 的参数 \(\gamma\) 作为 \(E[x]\) 了。而如果 ReLU 存在的话，就需要考虑 ReLU 这类函数对数据分布的影响。论文在附录里面用了较大篇幅推出了 ReLU 后的均值：

\[\begin{align} E[x_c]&=E[ReLU(x_c^{pre})] \tag{11} \\ &=\gamma_{c}N(\frac{-\beta_c}{\gamma_c}）+\beta_c[1-\Phi(\frac{-\beta_c}{\gamma_c})] \tag{12} \end{align} \]

对推导过程感兴趣的同学，可以自行查阅论文附录。同样地，如果你看了之后一阵眩晕，也不用太强迫自己一定要看懂，毕竟公式推导是数学家的事，工程师要做的是把搭建数学和现实之间的桥梁，把它们实现出来。

实验

这里摘取部分我比较关注的实验结果。

首先是 weight equalize + per-layer 和 per-channel 量化的效果对比，毕竟用 weight equalize 就是希望用 per-layer 达到或接近 per-channel 的效果：

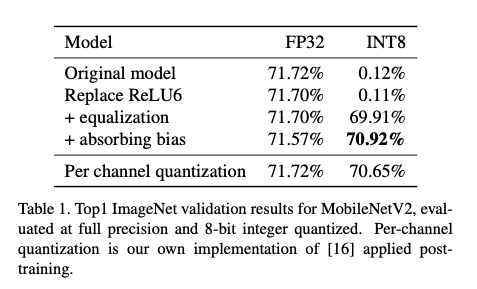
从 ImageNet 分类这个任务来看，在 MobilenetV2 这个网络上，weight equalize 和 per-channel 量化效果相当了。

我们也可以直观地感受下加上 weight equalize 后，权重是如何变化的。下图里面，左图是 MobilenetV2 里面，某个可分离卷积不同 kernel 的数值分布，右图是用上 weight equalize 后的数值分布，可以明显看到，用上 weight equalize 后，数值范围从 -50~100 的区间缩小到了 -0.75~0.75 的区间，这也正是 per-layer 量化时希望看到的结果：

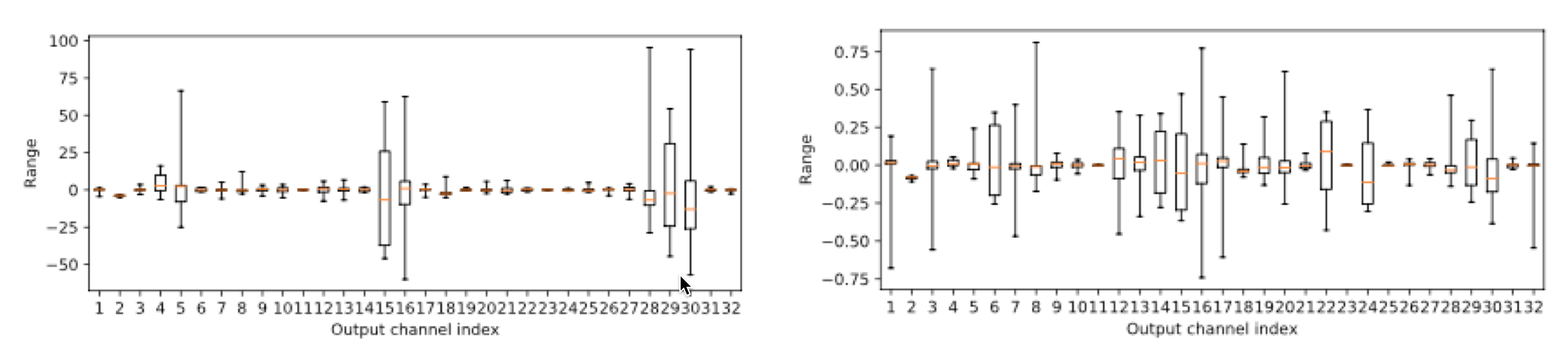
此外，我关注的另一个实验是，如果我们把卷积 kernel 中，那些大的 range 直接截断一部分，强制让每个 kernel 的数值接近，这样能不能取得好的结果呢？论文做的实验是强行把 kernel 的数值范围截断到 [-15, 15] 之间，然后对比和 weight equalize 的效果：

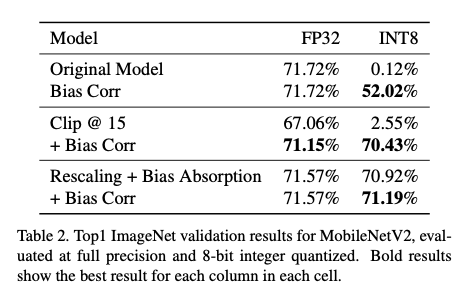
从结果来看，强行对 kernel 的数值进行截断，在没有重新训练的情况下，虽然全精度模型还能维持在 67% 的准确率上 (全精度只有 71%)，但量化后还是凉凉。如果截断到更小的范围，全精度的准确率应该要下降更多了，那量化后更没法比了。

论文还做了目标检测和分割的实验，结论基本类似，这里不再赘述。

不过，Bias Correction 对 weight equalize 的加持作用好像不明显啊。反倒是剪枝 (Clip@15) 和直接 per-layer 量化的情况中能带来很大的收益。这倒是给我带来一些启发，也许在一些模型剪枝压缩的任务中，可以考虑用上 Bias Correction。

总结

这篇文章主要介绍了高通 Data-Free 论文中的两个神技：Weight Equalization 和 Bias Correction。通过这些技巧，可以在卷积 (或者全连接层) 的 kernel 数值差异较大的情况下，用 per-layer 量化达到 per-channel 的效果。算法流程可以概括为下图：

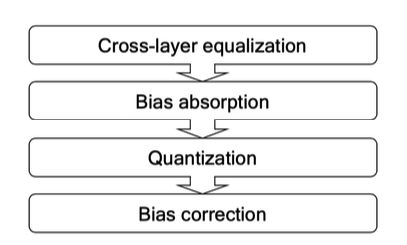
下一章中，我们挖一下 pytorch 源码，看看大佬们是怎么实现 Weight Equalization 和 Bias Correction 的，咱们下回见。

参考

1. Same, Same But Different - Recovering Neural Network Quantization Error Through Weight Factorization
2. https://zhuanlan.zhihu.com/p/104052236

欢迎关注我的公众号：大白话AI，立志用大白话讲懂AI。