Binary Tree
1.二叉树(含线索)的定义
typedef struct BTNode{ int data; int lTag;//0,左孩子;1,前驱 int rTag; struct BTNode *lchild; struct BTNode *rchild; }BTNode;
2.二叉树的遍历(递归形式)
void visit(BTNode *p){ cout<<p->data<<' '; } void pre_order(BTNode *p){ if(p!=NULL){ visit(p); pre_order(p->lchild); pre_order(p->rchild); } } void in_order(BTNode *p){ if(p!=NULL){ in_order(p->lchild); visit(p); in_order(p->rchild); } } void post_order(BTNode *p){ if(p!=NULL){ post_order(p->lchild); post_order(p->rchild); visit(p); } }
3.二叉的遍历(非递归)
递归中系统栈帮助完成了保护现场和恢复现场的工作,现在手动模拟系统栈的工作
void preorderNonrecursion(BTNode *bt){ if(bt !=NULL){ BTNode *Stack[maxSize]; int top=-1; BTNode *p=NULL; Stack[++top]=bt; while(top!=-1){ p=Stack[top--]; visit(p); if(p->rchild !=NULL){ Stack[++top]=p->rchild; } if(p->lchild !=NULL){ Stack[++top]=p->lchild; } } } } void postorderNonrecursin(BTNode * bt){ if(bt !=NULL){ BTNode *Stack1[maxSize];int top1=-1; BTNode *Stack2[maxSize];int top2=-1; BTNode *p=NULL; while(top1 !=-1){ p=Stack1[top1--]; Stack2[++top2]=p; //先序遍历和逆后续遍历相同,所有左右孩子顺序相反 if(p->lchild !=NULL){ Stack1[++top1]=p->lchild; } if(p->rchild!=NULL){ Stack1[++top1]=p->rchild; } } while(top2 !=-1){ p=Stack2[top2--]; visit(p); } } } void inorderNonrecursion(BTNode *bt){ if(bt !=NULL){ BTNode *Stack[maxSize];int top=-1; BTNode *p=NULL; p=bt; while(top!=-1||p!=NULL){ while(p!=NULL){ Stack[++top]=p; p=p->lchild; } if(top!=-1){ p=Stack[top--]; visit(p); p=p->rchild; } } } }
4.二叉树的层次遍历
void level(BTNode *bt){ if(bt !=NULL){ int front,rear; BTNode *que[maxSize]; front=rear=0; BTNode *p; rear=(rear+1)%maxSize; que[rear]=bt; while(front!=rear){ front=(front+1)%maxSize; p=que[front]; visit(p); if(p->lchild !=NULL){ rear=(rear+1)%maxSize; que[rear]=p->lchild; } if(p->rchild!=NULL){ rear=(rear+1)%maxSize; que[rear]=p->rchild; } } } }
5.二叉树的线索化
p为根节点,pre=NULL
void preThread(BTNode *p,BTNode *&pre){ if(p!=NULL){ if(p->lchild == NULL){ p->lchild=pre; p->lTag=1; } if(pre!=NULL&&pre->rchild==NULL){ pre->rchild=p; pre->rTag=1; } pre=p; if(p->lTag==0){ preThread(p,pre); } if(p->rTag==0){ preThread(p,pre); } } }
void inThread(BTNode *p,BTNode *&pre){ if(p!=NULL){ inThread(p->lchild,pre); if(p->lchild == NULL){ p->lchild=pre; p->lTag=1; } if(pre !=NULL &&pre->rchild){ pre->rchild=p; pre->rTag=1; } pre=p; inThread(p->rchild,pre); } }
void postThread(BTNode *p,BTNode *&pre){ if(p!=NULL){ postThread(p->lchild,pre); postThread(p->rchild,pre); if(p->lchild == NULL){ p->lchild=pre; p->lTag=1; } if(pre!=NULL && pre->rchild ==NULL){ pre->rchild=p; pre->rTag=1; } pre=p; } }
6.线索化二叉树的遍历
void preorder_pt(BTNode *tbt){ if(tbt!=NULL){ BTNode *p=tbt; while(p!=NULL){ while(p->lTag == 0){ visit(p); p=p->lchild; } } visit(p); p=p->rchild; } }
7.根据二叉树先中序遍历序列确定一颗二叉树
//根据先序,中序遍历序列确定二叉树 BTNode *CreateBT(char pre[],char in[],int L1,int R1,int L2,int R2){ if(L1>R1){ return NULL; } BTNode *s=(BTNode *)malloc(sizeof(BTNode)); s->lchild=s->rchild=NULL; s->data=pre[L1]; int i; for(int i=L2;i<=R2;++i){ if(in[i] == pre[L1]){ break; } } s->lchild=CreateBT(pre,in,L1+1,L1+i-L2,L2,i-1); s->rchild=CreateBT(pre,in,L1+i-L2+1,R1,i+1,R2); return s; }
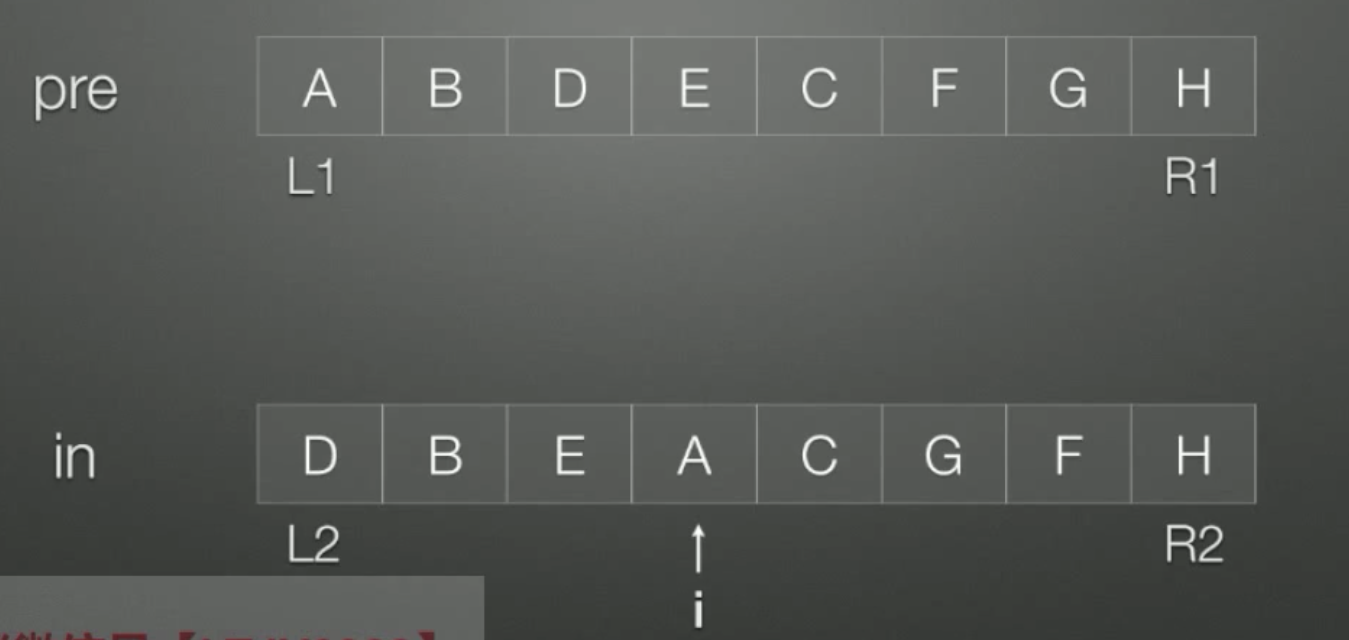

8.根据二叉树的后中序遍历序列确定二叉树
//根据后续,中序遍历序列确定二叉树 BTNode *CreateBT2(char post[],char in[],int L1,int R1,int L2,int R2){ if(L1>R1){ return NULL; } BTNode *s=(BTNode*)malloc(sizeof(BTNode*)); s->lchild=s->rchild=NULL; s->data=post[R1]; int i; for(i=L2;i<=R2;i++){ if(in[i] ==post[R1]){ break; } } s->lchild=CreateBT2(post,in,L1,L1+i-L2-1,L2,i-1); s->rchild=CreateBT2(post,in,L1+i-L2,R1-1,i+1,R2); }

9.根据二叉树的层次遍历和中序遍历序列确定二叉树

策略:根据中序遍历序列中的根结点划分子序列,其在层次遍历序列中是不连续的,把两部分不连续的结点挑出来,并保持其在层次遍历序列中的顺序,然后存入两个数组中,这样他们就连续了,之后在这两个数组中选出子树根结点,然后进行递归处理。


int search(char arr[],char key,int L,int R){ int idx; for(idx=L;idx<=R;idx++){ if(arr[idx] == key){ return idx; } } return -1; } void getSubLevel(char subLevel[],char level[],char in[],int n,int L,int R){ int k=0; for(int i=0;i<n;i++){ if(search(in,level[i],L,R) !=-1){ subLevel[k++]=level[i]; } } } //根据层次遍历和中序遍历确定二叉树 BTNode *CreateBT3(char level[],char in[],int n,int L,int R){ if(L>R){ return NULL; } BTNode *s=(BTNode*)malloc(sizeof(BTNode)); s->lchild=s->rchild=NULL; s->data=level[0]; int i=search(in,level[0],L,R); int LN=i-L;char LLevel[LN]; int RN=R-i;char RLevel[RN]; getSubLevel(LLevel,level,in,n,L,i-1); getSubLevel(RLevel,level,in,n,i+1,R); s->lchild=CreateBT3(LLevel,in,LN,L,i-1); s->rchild=CreateBT3(RLevel,in,RN,i+1,R); return s; }
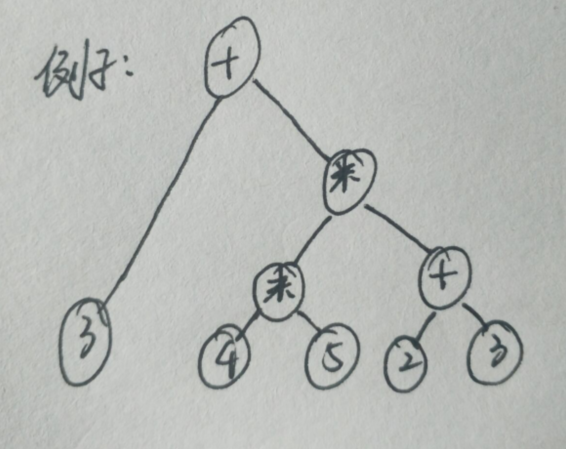
10.对存储了中缀表达式的二叉树求值
int calSub(float opand1,char op,float opand2,float &result){ if(op == '+') result=opand1+opand2; if(op == '-') result=opand1-opand2; if(op == '*') result=opand1*opand2; if(op == '/'){ if((fabs(opand2))<MIN){ return 0; }else{ result=opand1/opand2; } } return 1; } float cal(BTNode *root){ if(root->lchild==NULL&& root->rchild==NULL){ return root->data-'0'; }else{ float opand1=cal(root->lchild); float opand2=cal(root->rchild); float result; calSub(opand1,root->data,opand2,result); return result; } }
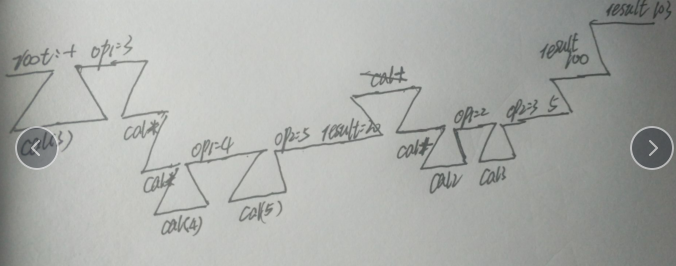
递归层次图



 浙公网安备 33010602011771号
浙公网安备 33010602011771号