机器学习(ML)三之多层感知机
多层感知机
深度学习主要关注多层模型,现在以多层感知机(multilayer perceptron,MLP)为例,介绍多层神经网络的概念。
隐藏层
多层感知机在单层神经网络的基础上引入了一到多个隐藏层(hidden layer)。隐藏层位于输入层和输出层之间。图展示了一个多层感知机的神经网络图。
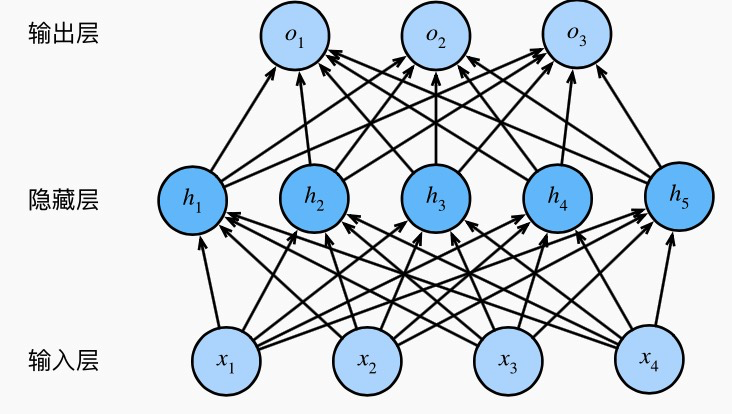

模型图所示的多层感知机中,输入和输出个数分别为4和3,中间的隐藏层中包含了5个隐藏单元(hidden unit)。由于输入层不涉及计算,模型图中的多层感知机的层数为2。由模型图可见,隐藏层中的神经元和输入层中各个输入完全连接,输出层中的神经元和隐藏层中的各个神经元也完全连接。因此,多层感知机中的隐藏层和输出层都是全连接层。
具体来说,给定一个小批量样本X∈ℝn×d,其批量大小为n,输入个数为d。假设多层感知机只有一个隐藏层,其中隐藏单元个数为h。记隐藏层的输出(也称为隐藏层变量或隐藏变量)为H,有H∈ℝn×h,因为隐藏层和输出层均是全连接层,可以设隐藏层的权重参数和偏差参数分别为Wh∈ℝd×h和bh∈ℝ1×h,输出层的权重和偏差参数分别W0∈ℝh×q和b0∈ℝ1×q
我们先来看一种含单隐藏层的多层感知机的设计。其输出![]() 的计算为
的计算为
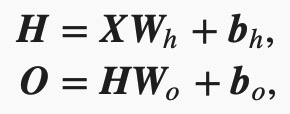
也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来,可以得到
![]()
从联立后的式子可以看出,虽然神经网络引入了隐藏层,却依然等价于一个单层神经网络:其中输出层权重参数为WhW0,偏差参数为bhW0+b。难发现,即便再添加更多的隐藏层,以上设计依然只能与仅含输出层的单层神经网络等价。
激活函数
上述问题的根源在于全连接层只是对数据做仿射变换(affine transformation),而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换,例如对隐藏变量使用按元素运算的非线性函数进行变换,然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数(activation function)。下面我们介绍几个常用的激活函数。
ReLU函数
ReLU(rectified linear unit)函数提供了一个很简单的非线性变换。给定元素xx,该函数定义为
![]()
可以看出,ReLU函数只保留正数元素,并将负数元素清零。为了直观地观察这一非线性变换,我们先定义一个绘图函数xyplot。
%matplotlib inline import d2lzh as d2l from mxnet import autograd, nd def xyplot(x_vals, y_vals, name): d2l.set_figsize(figsize=(5, 2.5)) d2l.plt.plot(x_vals.asnumpy(), y_vals.asnumpy()) d2l.plt.xlabel('x') d2l.plt.ylabel(name + '(x)')
我们接下来通过NDArray提供的relu函数来绘制ReLU函数。可以看到,该激活函数是一个两段线性函数。
x = nd.arange(-8.0, 8.0, 0.1) x.attach_grad() with autograd.record(): y = x.relu() xyplot(x, y, 'relu')

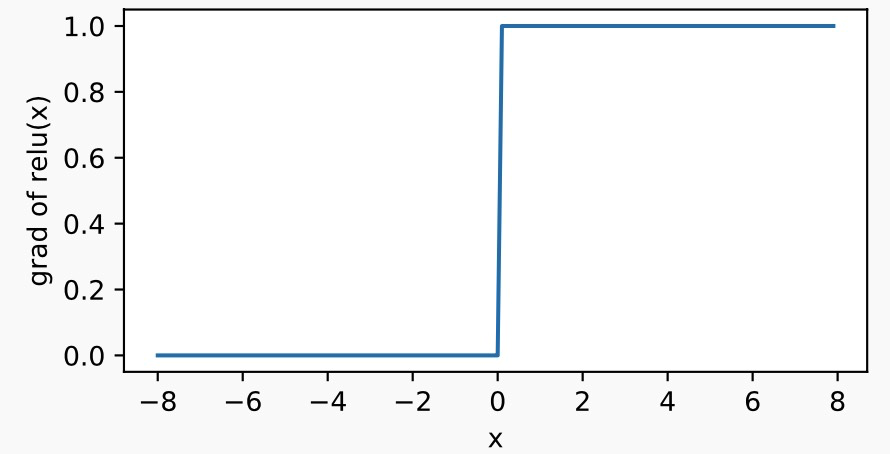
显然,当输入为负数时,ReLU函数的导数为0;当输入为正数时,ReLU函数的导数为1。尽管输入为0时ReLU函数不可导,但是我们可以取此处的导数为0。下面绘制ReLU函数的导数。
y.backward() xyplot(x, x.grad, 'grad of relu')
sigmoid函数
sigmoid函数可以将元素的值变换到0和1之间:
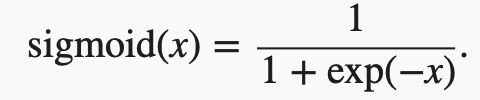
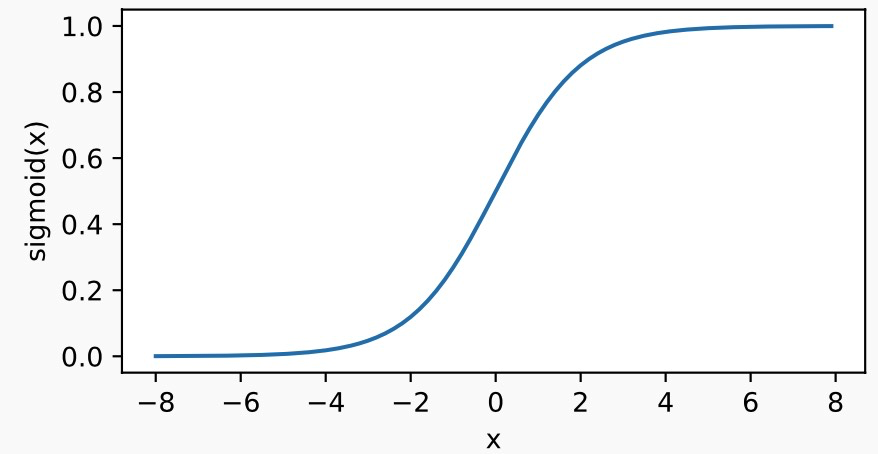
sigmoid函数在早期的神经网络中较为普遍,但它目前逐渐被更简单的ReLU函数取代。在后面“循环神经网络”一章中我们会介绍如何利用它值域在0到1之间这一特性来控制信息在神经网络中的流动。下面绘制了sigmoid函数。当输入接近0时,sigmoid函数接近线性变换。
with autograd.record(): y = x.sigmoid() xyplot(x, y, 'sigmoid')
依据链式法则,sigmoid函数的导数
![]()
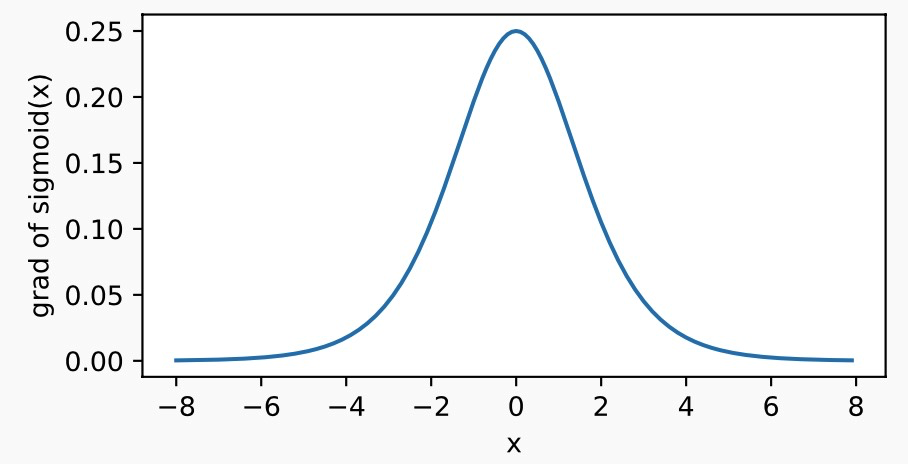
下面绘制了sigmoid函数的导数。当输入为0时,sigmoid函数的导数达到最大值0.25;当输入越偏离0时,sigmoid函数的导数越接近0。
y.backward() xyplot(x, x.grad, 'grad of sigmoid')
tanh函数
tanh(双曲正切)函数可以将元素的值变换到-1和1之间:

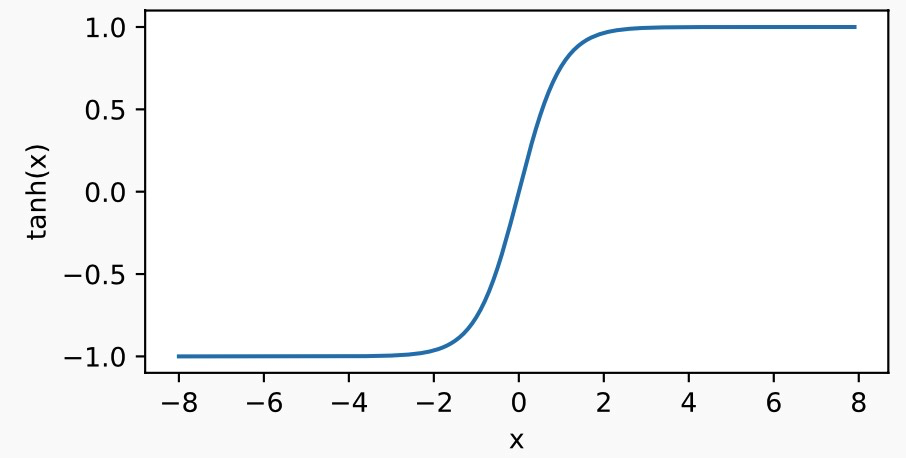
绘制tanh函数。当输入接近0时,tanh函数接近线性变换。虽然该函数的形状和sigmoid函数的形状很像,但tanh函数在坐标系的原点上对称。
with autograd.record(): y = x.tanh() xyplot(x, y, 'tanh')
依据链式法则,tanh函数的导数
![]()
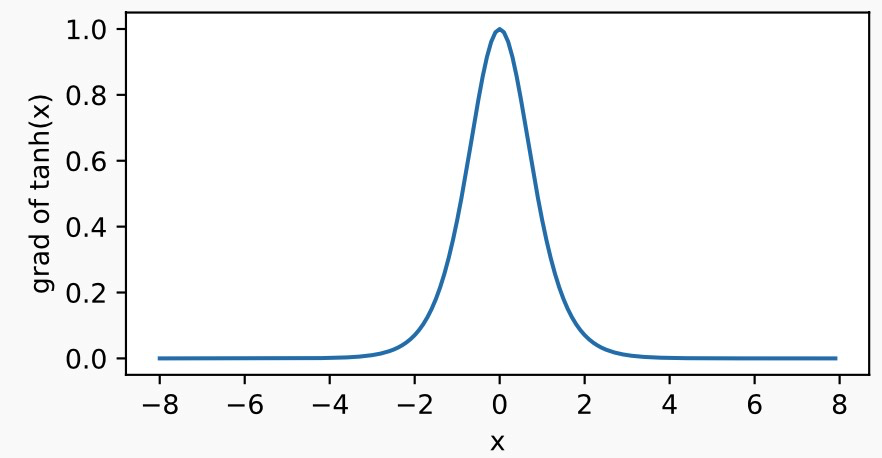
绘制了tanh函数的导数。当输入为0时,tanh函数的导数达到最大值1;当输入越偏离0时,tanh函数的导数越接近0。
y.backward() xyplot(x, x.grad, 'grad of tanh')
多层感知机
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号,多层感知机按以下方式计算输出:
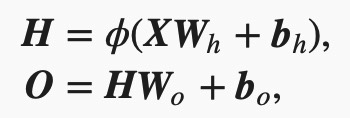
其中ϕ表示激活函数。在分类问题中,我们可以对输出O做softmax运算,并使用softmax回归中的交叉熵损失函数。 在回归问题中,我们将输出层的输出个数设为1,并将输出O直接提供给线性回归中使用的平方损失函数。
代码实现
#!/usr/bin/env python # coding: utf-8 # In[1]: get_ipython().run_line_magic('matplotlib', 'inline') import d2lzh as d2l from mxnet import nd from mxnet.gluon import loss as gloss # In[2]: #读取数据 batch_size = 256 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # In[3]: #定义模型参数 #Fashion-MNIST数据集中图像形状为28×28,类别数为10。我们使用长度为28×28=784的向量表示每一张图像。 #因此,输入个数为784,输出个数为10。实验中,我们设超参数隐藏单元个数为256。 num_inputs, num_outputs, num_hiddens = 784, 10, 256 W1 = nd.random.normal(scale=0.01, shape=(num_inputs, num_hiddens)) b1 = nd.zeros(num_hiddens) W2 = nd.random.normal(scale=0.01, shape=(num_hiddens, num_outputs)) b2 = nd.zeros(num_outputs) params = [W1, b1, W2, b2] for param in params: param.attach_grad() # In[4]: #定义激活函数 def relu(X): return nd.maximum(X, 0) # In[6]: #定义模型 def net(X): X = X.reshape((-1, num_inputs)) H = relu(nd.dot(X, W1) + b1) return nd.dot(H, W2) + b2 # In[8]: #定义损失函数 loss = gloss.SoftmaxCrossEntropyLoss() # In[9]: #训练模型 num_epochs, lr = 5, 0.5 d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号