面向对象课程第一单元作业总结

面向对象课程第一单元作业总结

—— 表达式求导的进击之路

---

前言

面向对象课程的前三次作业是表达式求导的不断进阶的过程。本文从思路、代码度量分析、Bug发现、阶段思考等方面对三次作业逐个进行分析总结，最后再针对第三次作业探讨工厂模式的应用。

目录

• 一、第一次作业 —— Java编程初探
• 二、第二次作业 —— 懒人式扩展代码
• 三、第三次作业 —— 面向对象编程入门
• 四、对象创建模式应用尝试

一、第一次作业 —— Java编程初探

1. 思路

第一次的作业麻雀虽小，但五脏俱全。因为是第一次写Java程序，笔者很用心地思考了一下层序的结构。

首先，确定程序的总体结构。在上个学期的《Ruby程序设计语言》和《数据库课程设计》课程中接触到了web开发时使用的MVC模式，于是想到把这种模式应用到本次作业中来。具体方法是定义三个类，Model模块用来处理表达式数据的存储和求导（Polynomial），View模块用来处理控制台的输入数据（Expression），Control模块用来协调程序运行逻辑（Main）。

其次，识别表达式的方法。在拿到这个题目的时候，笔者第一反应是《编译原理》的递归下降子表达式那一套，但是后来经过指导书的提醒，决定使用正则表达式进行表达式的识别。

再次，多项式存储数据结构设计。笔者使用HashMap存储多项式，以指数（exponent）作为Key，系数（coefficient）作为value。一来本次作业比较简单，这样的结构足够存储表达式；二来这样设计有利于优化时同类项的合并（实际上在识别表达式的过程中就可以进行表达式同类项的合并）。

然后，大数处理。这个倒是很容易，使用Java自带的 BigInteger 类即可。

最后，优化方法。本次作业复杂度有限，因此优化方法也很简单，只包含输出过程中的优化。秉承下面几个原则即可：

• 尽量使输出的第一个项为正（减小一个 + 的长度）；
• 确保两项之间只有一个运算符号；
• 处理项系数或指数为 1 或 0 或 -1 时的特殊情况；
• 为了保证正确性，在没有输出任何项的时候，输出 "0"。

2. 代码度量分析

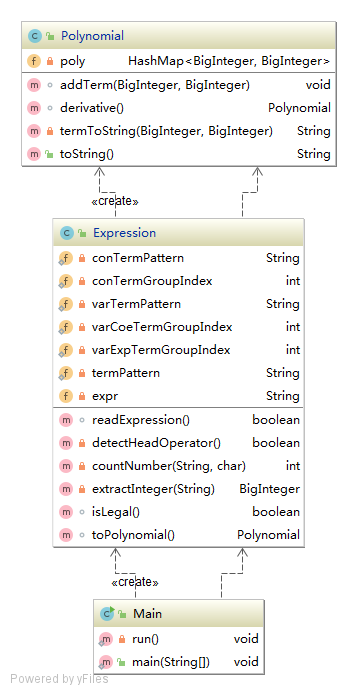
类及其依赖关系

方法复杂度

Method	ev(G)	iv(G)	v(G)
polynomial.Expression.countNumber(String,char)	1	2	3
polynomial.Expression.detectHeadOperator()	1	1	1
polynomial.Expression.extractInteger(String)	1	3	4
polynomial.Expression.isLegal()	1	1	1
polynomial.Expression.readExpression()	1	2	4
polynomial.Expression.toPolynomial()	1	4	4
polynomial.Main.main(String[])	1	1	1
polynomial.Main.run()	1	3	3
polynomial.Polynomial.addTerm(BigInteger,BigInteger)	1	3	3
polynomial.Polynomial.derivative()	1	3	3
polynomial.Polynomial.termToString(BigInteger,BigInteger)	1	9	11
polynomial.Polynomial.toString()	1	4	6
Total	12	36	44
Average	1	3	3.67

从上面的类图可以看出框架大致是按照 MVC 模式设计的，基本达到预期效果。但是在对类方法进行度量分析的时候，笔者发现 Polynomial.termToString() 方法的圈复杂度超标。那么圈复杂度是个什么东西呢？经过百度，圈复杂度是用来衡量一个模块判定结构的复杂程度的量，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护。

经过检查代码发现，在该方法中存在如下的判断逻辑：

	...
	if (coe.compareTo(zero) != 0) {
	    // ignore (coe) when exp != 0 and coe == 1 or -1
	    if (exp.compareTo(zero) == 0) {
	        tmpString = coe.toString();
	    } else {
	        if (coe.compareTo(negOne) == 0) {
	            tmpString = "-";
	        }
	        else if (coe.compareTo(posOne) != 0) {
	            tmpString = coe.toString();
	        }
	    }
	    // ignore (*) when exp == 0 or coe == 1 or coe == -1
	    if (exp.compareTo(zero) != 0 &&
	        coe.compareTo(posOne) != 0 &&
	        coe.compareTo(negOne) != 0) {
	        tmpString = tmpString + "*";
	    }
	    // ignore (x) when exp == 0
	    if (exp.compareTo(zero) != 0) {
	        tmpString = tmpString + "x";
	    }
	    // ignore (^exp) when exp == 0 or 1
	    if (exp.compareTo(zero) != 0 && exp.compareTo(posOne) != 0) {
	        tmpString = tmpString + "^" + exp.toString();
	    }
	}
	...

这段代码用于输出一个 term ，具体方法是将一个项的输出分成四个部分 (op)(coe)(*)(x)(^exp) ，根据不同的系数和指数判断各个部分是否需要输出，从而得到最短结果，比如当系数是 1 的时候省略系数和 (coe) 和 (*)。这段代码虽然判断逻辑有些复杂，但实际上思路很清晰（恬不知耻地自认为），所以勉强也是可以接受的。

3. Bug发现

在公测中并没有发现Bug。不参与互测。

本次作业非常简单，去掉空格和注释后，纯代码量为204行，所以测试也非常简单。

主要分为两个部分进行测试，一是表达式合法性检查，二是表达式运算结果检查。

4. 作业小结

本次作业实现过程中实际上没有使用到多少面向对象的机制。表面上通过类之间的调用来实现，只不过是将功能相近的过程封装到一个类中了，本质上还是过程式编程。所以基本上没有什么面向对象的思想可以应用到本次作业中来。通过这次作业，笔者得到的最大收获是Java语言的正则表达式。有句未知来源的话说得很在理：

Let’s say you have a problem, and you decide to solve it with regular expressions. Well, now you have two problems.

下面对在作业中遇到的正则表达式相关的问题进行详细的阐述。

可读性

正则表达式的功能非常强大，但是在做一些稍微复杂的字符串匹配的时候，正则表达式的复杂度也会随之提高。如此一来，正则表达式很容易变成一长串糟糕的多层括号嵌套的字符串。以这次作业的正则表达式为例，按照指导书规定写出来的正则表达式为((\s*(([+-]\s*[+-]?(\d+\s*\*)?\s*)x((\s*\^\s*[+-]?\d+)?))|(\s*[+-]\s*[+-]?\d+))\s*)++。私以为这不是适合人类阅读的代码。

于是，笔者在作业中使用了分层次拼接正则表达式的方法。如下：

public class Expression {
    private static String conTermPattern;
    private static String varTermPattern;
    private static String termPattern;
    ...
    static {
        conTermPattern = "(\\s*[+-]\\s*[+-]?\\d+)";
        String signedCoefficientPattern = "([+-]\\s*[+-]?(\\d+\\s*\\*)?\\s*)";
        String signedExponentPattern = "((\\s*\\^\\s*[+-]?\\d+)?)";
        varTermPattern = String.format("\\s*(%sx%s)",
            signedCoefficientPattern, signedExponentPattern);
        termPattern = String.format("(%s|%s)\\s*",
            varTermPattern, conTermPattern);
		...
    }
	...
}

这样一来使得正则式的层次更加清晰，也增加了代码的可读性和可维护性。

Java正则表达式的三种模式

在进行输入字符串合法性判断的时候需要使用 (termPattern)+ 对整个表达式进行匹配，然而遇到字符串过长的时候就会报 java.lang.StackOverflowError 的异常。

经过百度，发现原来Java正则表达式有三种不同的匹配模式，贪婪模式（默认），懒惰模式和独占模式。三种模式的具体含义不再赘述，具体书写方式是在正则表达式的 +、*、?、{} 后面添加特殊字符即可。懒惰模式添加 ? ，独占模式添加 + 。

当把贪婪模式转换成独占模式的时候，正则表达式引擎每成功匹配到一个最长字符串便会将状态归零，不会像贪婪模式一样将已经匹配的字符一直缓存下来，占用大量空间，造成栈溢出。

所以，将 (termPattern)+ 修改为 (termPattern)++ 便能够解决栈溢出的问题（情不自禁，真香！）。

二、第二次作业 —— 懒人式扩展代码

1. 思路

第二次作业相对于第一次作业增加了乘法规则和正余弦三角函数。在本质上和第一次作业区别不大，于是便直接在第一次作业的基础上做了扩展。大致思路和第一次作业相同，只是在多项式存储数据结构、优化方法和求导方法上做了修改。

多项式存储数据结构

采用两级存储结构，底层是 Term 类，以三元组的形式保存 x，sin(x) 和 cos(x)的指数，表示三项相乘；上层是 Expression 类，使用 HashMap<Term, BigInteger> 来保存 Term 和它对应的系数，表示各项相加。这样的设计适合同类项的合并，但是不适合三角函数的化简，并且扩展性很差。

优化方法

优化可以划分为两个部分，同类项合并和三角函数特殊优化。

关于同类项合并，很容易可以观察到只有两项的自变量 x，正弦函数 sin(x) 和余弦函数 cos(x)各项指数分别相等的时候，能够进行合并。使用以 Term 为Key，coefficient 为value的 HashMap 可以很方便实现这种同类项合并，但是这种方法也带来了一定的弊端，也相当不优雅，后面会讲到这一点。

关于三角函数化简，讨论区大佬们提出各种各样的方案，甚至有人提到了遗传算法。表达式的最终化简结果将会和项合并的顺序和拆分方法有关。笔者意识到将表达式化简到最简形式将会大大增加代码量和程序复杂度，所以采用了贪心的近似算法（实际上并不是很接近最优解），指导思想是 \(sin(x)^{2}+cos(x)^{2}=1\) ，循环进行扫描发现可合并的两项，算法复杂度为\(O(n^{2})\)（这里不再详细论证）。由于笔者采用的化简方法是在当前对象上直接进行修改，所以还需要一点点小技巧处理迭代器的问题，不再赘述。

对于两个表达式项：

\[a_1*x^{b_1}*sin(x)^{c_1}*cos(x)^{d1} \]

\[a_2*x^{b_2}*sin(x)^{c_2}*cos(x)^{d2} \]

二者能够进行拆分合并的条件是：

\[c_1 - c_2 = d_2 - d_1 = 2 或 -2 \]

当两个表达式项满足合并条件时，出现三种处理方案：

1. 当\(a_1=a_2\)时，直接将两项系数相加完成合并；
2. 当\(a_1 \not=a_2\)时，拆分系数为 \(a_1\) 的项成为为系数为 \(a_2\) 和 \((a_1-a_2)\) 的两项，将此时将此时两个系数相同的项合并；
3. 当\(a_1 \not=a_2\)时，拆分系数为 \(a_2\) 的项，合并同系数的两项。

针对上面的三种方法，分别计算出合并之后的表达式输出长度，选择输出长度最小的方式。

这种方式显然很难达到最优解，比如对于表达式 \(sin(x)^{4}+2*sin(x)^{2}*cos(x)^{2}+cos(x)^{4}\) 我们期待的最优解是 \(1\) ，但是最后化简出的结果很有可能是 \(2*sin(x)^{2}+cos(x)^{4}-sin(x)^{4}\)。

求导方法

第二次作业在表达式求导的加法规则上添加了乘法规则。因为本次作业的特殊性 —— 每一项最多只有三个非常数函数相乘，所以直接套用公式

\[(f*g*h)'=f'*g*h+f*g'*h+f*g*h' \]

2. 代码度量分析

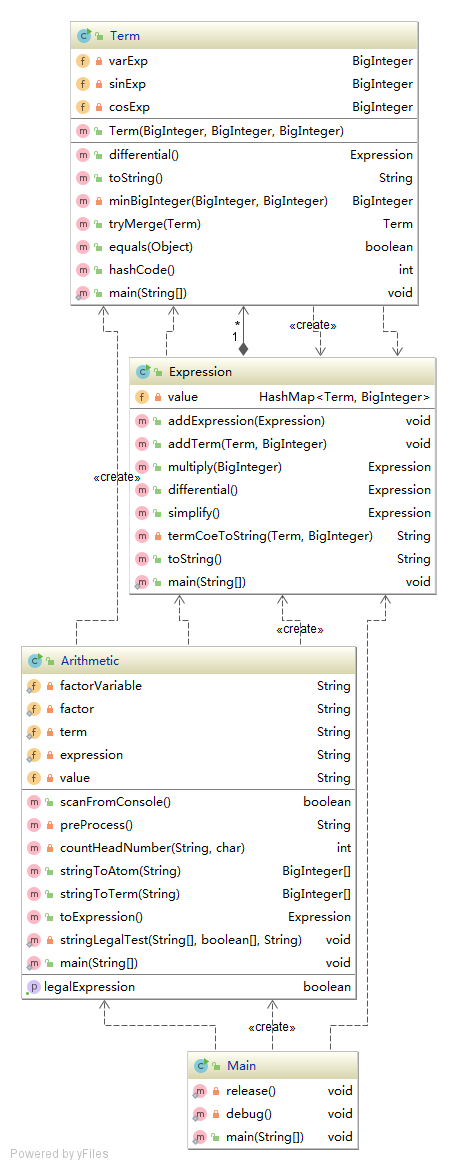
类及其依赖关系

方法复杂度

Method	ev(G)	iv(G)	v(G)
differential.Arithmetic.countHeadNumber(String,char)	1	3	4
differential.Arithmetic.isLegalExpression()	1	1	1
differential.Arithmetic.main(String[])	1	1	1
differential.Arithmetic.preProcess()	1	1	2
differential.Arithmetic.scanFromConsole()	1	1	2
differential.Arithmetic.stringLegalTest(String[],boolean[],String)	1	3	3
differential.Arithmetic.stringToAtom(String)	1	7	7
differential.Arithmetic.stringToTerm(String)	1	3	4
differential.Arithmetic.toExpression()	1	2	2
differential.Expression.addExpression(Expression)	1	2	2
differential.Expression.addTerm(Term,BigInteger)	1	3	3
differential.Expression.differential()	1	2	2
differential.Expression.main(String[])	1	1	1
differential.Expression.multiply(BigInteger)	1	3	3
differential.Expression.simplify()	10	7	13
differential.Expression.termCoeToString(Term,BigInteger)	2	9	9
differential.Expression.toString()	2	5	6
differential.Main.debug()	1	3	3
differential.Main.main(String[])	1	1	1
differential.Main.release()	1	3	3
differential.Term.Term(BigInteger,BigInteger,BigInteger)	1	1	1
differential.Term.differential()	1	1	1
differential.Term.equals(Object)	2	4	4
differential.Term.hashCode()	1	1	1
differential.Term.main(String[])	1	1	1
differential.Term.minBigInteger(BigInteger,BigInteger)	1	1	2
differential.Term.toString()	1	7	7
differential.Term.tryMerge(Term)	1	6	6
Total	40	83	95
Average	1.43	2.96	3.39

类图方面，由于第二次作业仅仅在第一次作业的基础上做了简单的扩展，所以两者类图基本相似。

代码度量方面，第二次作业仍然存在第一次作业中输出方法复杂度过高的问题，而且还出现了新的问题。differential.Expression.simplify()方法复杂度超标，经过排查代码发现此代码中为了实现上面叙述的复杂度为 \(O(n^{2})\) 的优化算法，使用了三层循环进行扫描可合并项，循环内部还存在条件判断分支来选择三种合并方案中的一种，此方法长度达到近60行。目前想到的方法是将条件分支拆分到一个新的函数中，实现方法功能的单一化，降低复杂度。

虽然出现了上面的问题，但是总体上而言代码结构实现了“高内聚，低耦合”。

3. Bug发现

由于在第二次作业上偷了不少懒，所以果不其然出现了Bug。

该Bug出现在识别出表达式项之后将字符串转化为系数和指数等数据的过程中，具体原因是项系数正负判断的漏洞。由于第一次作业的特性，在识别出系数字符串之后将字符串交给 differential.Arithmetic.countHeadNumber(String,char) 方法，该方法逐个字符检查记录 '-' 出现次数并返回，以此便能够判断系数正负；但是对于第二次作业，传递给该方法的字符串不再是系数字符串，而是项字符串，这时候仍然计算整个字符串中 '-' 出现次数，就导致会有其它常数的符号影响系数符号的计次。于是，本次作业在强测中错了两个点（感觉还是很幸运？）

这个Bug出现的位置是在 MVC 设计模式中的 View 部分。在第一次作业向第二次作业的扩展过程中，这一部分的代码实际上不需要太大的修改，所以就放松了警惕。而且在第一次作业的代码书写过程中，仅仅考虑了当次代码的实现逻辑是否正确，而没有考虑代码的普适性和扩展性，这也是出现Bug的原因之一。当然最大的问题还是因为测试马虎，前三次作业都是使用了很原始的构造数据样例，写 main 函数进行测试，这样进行的测试过程繁琐消磨意志，计划在后面的作业中使用Junit进行代码的测试。

4. 作业小结

除了吸取了两个点 WA 的教训之外，其他的没什么好总结的。

本次作业相对于第一次作业在代码架构没有本质上的突破，仍然是一个披着面向对象外衣的面向过程编程。一来是因为业务逻辑比较简单，二来是因为对Java面向对象的机制一知半解。但是已经能够意识到这个架构扩展的局限性，到了第三次作业的时候，这座小破茅屋自然要推倒重建了。

三、第三次作业 —— 面向对象编程入门

1. 思路

第三次作业由于加入了嵌套规则，难度陡然上升。笔者将从代码架构、表达式识别和优化方法方面具体阐述本次作业 的思路。

代码架构

先来承接上文，前面说使用三元组哈希表来存储的表达式相当不优雅，这是为什么呢？一来，常数也是表达式项各个乘法元素的一个因子，为什么要把常数从中剥离开，塞到哈希表的value字段中呢？二来，如果要在现有代码的基础上实现新的需求，我们只能对现有的Term类进行修改，添加一个新的域，表示新函数的指数，现在问题来了，幂函数也是函数，凭什么它就如此特殊，能够用来组织表达式项的存储结构呢？而且这是很典型的面向过程式思维——使用不同的域来表示不同的对象，更不用说这种扩展方式严重违反了“开闭原则”。

经过上面的分析，笔者大致确定了代码架构的大致方向：

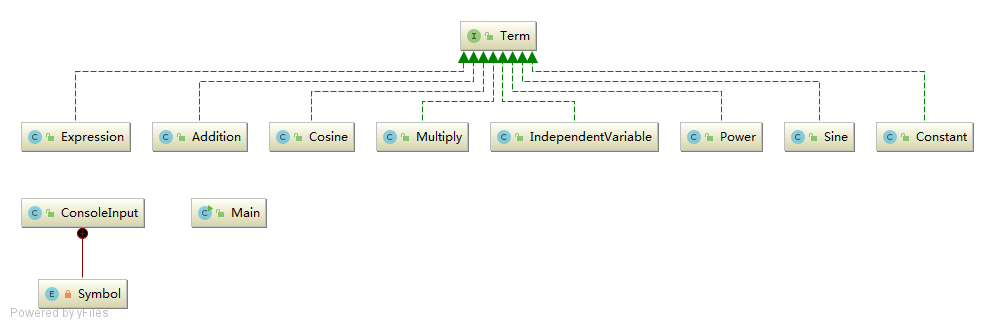
• 保持 MVC 框架不改变。不同于前两次作业使用类来划分框架结构，本次作业使用包结构来体现 MVC 框架结构，即在顶层包下有两个包（分别为engine和parse）和一个总控逻辑main类。engine包用于处理表达式存储和求导计算，parse用于实现识别并解析控制台输入的表达式。
• 将所有的函数抽象出来，一视同仁。将所有的函数都看作加减乘除一样的运算符，它们都实现同一个接口。实现接口的目的是实现各函数类的统一访问。不同的是分为单目运算符和多目运算符，甚至有零目运算符。单目运算符包括三角函数，多目运算符包括加法乘法等运算，零目运算符（常量）包括自变量 \(x\) 和常数。

表达式识别

第三次作业的表达式规则中添加了嵌套规则，表达式包含项，而项中又包含表达式，所以Java正则表达式机制便不再能够很好地支持表达式字符串的解析工作了。于是只好回到最初的起点——递归下降子函数法（感恩《编译原理》）。该方法最后得到的表达式存储结构是多层次的树形结构。笔者构造的文法规则如下：

<expression> = [+-]?<term>([+-]<term>)*
<term> = [+-]?<factor>(<factor>)*
<factor> = <conFactor>|<varFactor>|<powerFactor>|<triFactor>|<exprFactor>
<conFactor> = [+-]?\d+
<varFactor> = x
<powerFactor> = <varFactor>[^<conFactor>]
<triFactor> = (sin|cos(<factor>))[^<conFactor>]
<exprFactor> = (<expression>)

虽然正则表达式不能一站式解决表达式解析的问题，但是有了正则表达式的加持，递归下降子程序法在识别表达式符号也轻松了不不少。

优化方法

由于第三次作业的重点不在于表达式输出的优化（实际上也很难演算出表达式的最简形式），所以笔者仅仅做了第一次作业中类似的输出优化。

值得一提的是，虽然表达式输出优化比较困难，上升空间非常有限，但是表达式存储结构的优化对于程序而言非常重要。在递归下降子程序自动解析表达式字符串的时候形成的表达式存储树存在大量的冗余嵌套。例如，我们期待的 \(sin(x)\) 的存储方式是一个正弦函数类，但是实际上解析得到的结果经常是一个加法类，加法类中包含一个乘法类，在这个乘法类中才是正弦函数列，显然就出现了很不必要的冗余的嵌套。

仔细思考之后会发现，这种冗余是采用递归下降子程序方法解析字符串和树形结构存储表达式的天然缺陷。冗余的嵌套必然会造成后面代码调试和优化上巨大的资源开销。

其实想要解决这个问题也非常简单，本文提出的解决方案是在每个类的构造函数中调用其value的simplify方法，从源头斩断多层冗余嵌套出现的可能性。

2. 代码度量分析

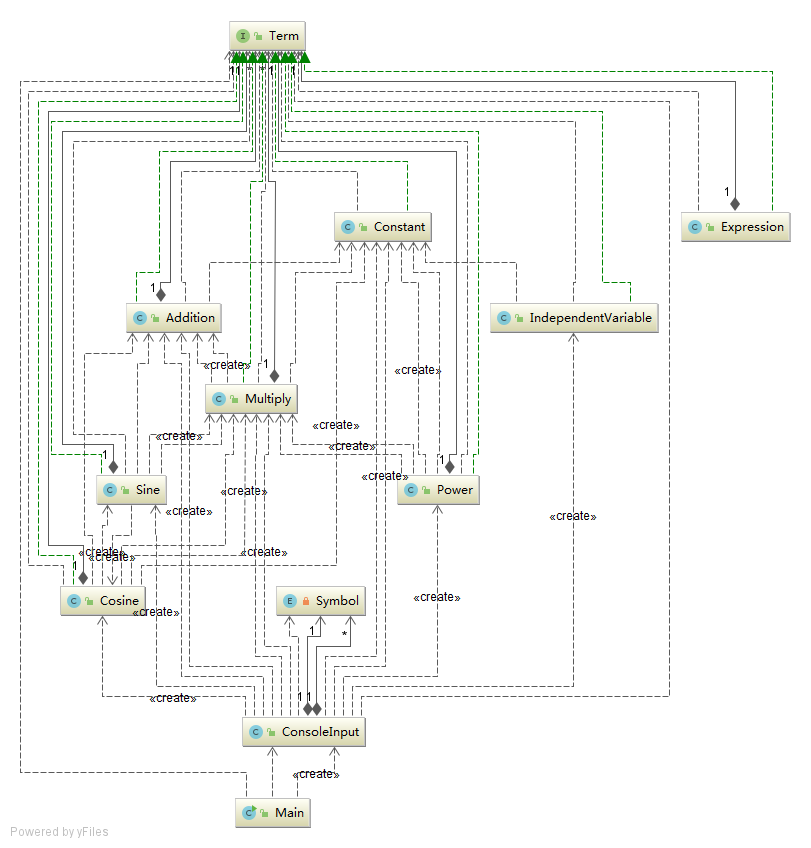
类图及其简化版

类间依赖关系

方法复杂度

Method	ev(G)	iv(G)	v(G)
differiential.Main.debug()	1	2	2
differiential.Main.main(String[])	1	1	1
differiential.Main.release()	1	3	3
differiential.Main.wrongFormatInfo()	1	1	1
differiential.engine.Addition.addTerm(Addition)	1	2	2
differiential.engine.Addition.addTerm(Term)	1	3	3
differiential.engine.Addition.clone()	1	2	2
differiential.engine.Addition.detectNegOp(String)	4	2	4
differiential.engine.Addition.differential()	1	2	2
differiential.engine.Addition.isEmpty()	4	3	4
differiential.engine.Addition.mergeConstant()	1	4	4
differiential.engine.Addition.simplify()	1	3	3
differiential.engine.Addition.toString()	1	5	5
differiential.engine.Constant.Constant(BigInteger)	1	1	1
differiential.engine.Constant.Constant(long)	1	1	1
differiential.engine.Constant.add(Constant)	1	1	1
differiential.engine.Constant.clone()	1	1	1
differiential.engine.Constant.compareTo(long)	1	1	1
differiential.engine.Constant.differential()	1	1	1
differiential.engine.Constant.equals(Object)	2	2	2
differiential.engine.Constant.getValue()	1	1	1
differiential.engine.Constant.mul(Constant)	1	1	1
differiential.engine.Constant.simplify()	1	1	1
differiential.engine.Constant.toString()	1	1	1
differiential.engine.Cosine.Cosine(Term)	1	1	1
differiential.engine.Cosine.clone()	1	1	1
differiential.engine.Cosine.differential()	1	1	1
differiential.engine.Cosine.simplify()	1	1	1
differiential.engine.Cosine.toString()	1	2	3
differiential.engine.Expression.Expression(Term)	1	1	1
differiential.engine.Expression.clone()	1	1	1
differiential.engine.Expression.differential()	1	1	1
differiential.engine.Expression.simplify()	1	1	1
differiential.engine.Expression.toString()	1	1	1
differiential.engine.IndependentVariable.clone()	1	1	1
differiential.engine.IndependentVariable.differential()	1	1	1
differiential.engine.IndependentVariable.simplify()	1	1	1
differiential.engine.IndependentVariable.toString()	1	1	1
differiential.engine.Multiply.clear()	1	1	1
differiential.engine.Multiply.clone()	1	2	2
differiential.engine.Multiply.differential()	1	4	4
differiential.engine.Multiply.mergeConstant()	1	5	5
differiential.engine.Multiply.mulTerm(Term)	1	4	4
differiential.engine.Multiply.simplify()	1	3	3
differiential.engine.Multiply.toString()	3	9	9
differiential.engine.Power.Power(Term,BigInteger)	1	1	1
differiential.engine.Power.Power(Term,Constant)	1	1	1
differiential.engine.Power.clone()	1	1	1
differiential.engine.Power.differential()	1	1	1
differiential.engine.Power.simplify()	1	1	1
differiential.engine.Power.toString()	1	3	3
differiential.engine.Sine.Sine(Term)	1	1	1
differiential.engine.Sine.clone()	1	1	1
differiential.engine.Sine.differential()	1	1	1
differiential.engine.Sine.simplify()	1	1	1
differiential.engine.Sine.toString()	1	2	3
differiential.parse.ConsoleInput.conFactor()	1	2	2
differiential.parse.ConsoleInput.errorHandler()	1	1	1
differiential.parse.ConsoleInput.exprFactor()	1	2	2
differiential.parse.ConsoleInput.expression()	1	5	6
differiential.parse.ConsoleInput.factor()	1	6	7
differiential.parse.ConsoleInput.getSymbol(int)	2	3	4
differiential.parse.ConsoleInput.powerFactor()	1	4	4
differiential.parse.ConsoleInput.scanFromConsole()	1	2	3
differiential.parse.ConsoleInput.term()	1	4	4
differiential.parse.ConsoleInput.toExpression()	1	2	2
differiential.parse.ConsoleInput.triFactor()	1	7	9
differiential.parse.ConsoleInput.varFactor()	1	1	1
Total	78	141	152
Average	1.15	2.07	2.24

从上面的度量分析来看，本次作业的70多个方法中仅仅有三个因为复杂度超标而标红，其中differiential.engine.Multiply.toString()方法是因为输出逻辑过于复杂，可以通过拆分函数的方法来解决，另外两个方法都是不超过10行代码的方法由于循环内包含分值判断造成的复杂度偏高，也很好修正。

总体而言，本次作业相对于上面的两次作业，平均复杂度的各项指标都有所下降，基本符合“高内聚，低耦合”的设计理念。

3. Bug发现

不参与互测，弱测和强测均没有发现Bug。

虽然本次作业的弱测和强测都没有发现Bug，但是其中仍然存在一些令人不安的因素。起因是在书写代码的过程中没有特别注意可变对象和不可变对象的区别，于是造成了下面的问题：

• 增加了对象克隆的复杂性。每个对象实际上都是一个表达式存储树的根节点，它下面存在很多子节点，其中有可变对象，也有不可变对象。在深拷贝的过程中由于没有很好地区分可变对象和不可变对象，所以很容易出现引用混乱的情况。
• 存储树结构混乱。在本次作业的表达式存储树中出现同一个对象被不同层次的树节点引用，或被同一层次的不同结点引用的情况。虽然只要保证对可变对象的修改都是等价修改（修改前后对象表示的表达式等价）就能保证程序运行的正确性（实际上也是这样做的），而且还能够在一定程度上减小程序的时间和空间复杂度，但是这始终不是一种令人放心的、对扩展友好的、优雅的代码实现方式。

那么怎么解决这个问题呢？笔者认为应该尽量使用不可变对象来代替可变对象，或使用多级继承结构来区分可变和不可变对象。

4. 作业小结

前两次作业都是披着面向对象外衣的面向过程式编程，到第三次作业才使用了接口等机制，变成了一次真正的面向对象式编程。深刻地感受到接口统一访问对于面向对象的重要意义。

还有一个关于静态成员变量的小技巧。前两次作业中为了实现大数的判零或判一，笔者都是新创建一个 \(0\) 或 \(1\) 的 BigInteger对象，然后使用BigInteger.compareTo()方法进行比较（求大佬们偷偷笑，不要出声）。直到读了BigInteger类的源码之后才发现人家已经给定义好了BigInteger.ZERO和BigInteger.ONE。将常用的对象设置为静态成员变量能够避免在每次使用的时候先创建一个对象造成不必要的开销；还能大大简化代码，提升美感。

除此之外，在第三次作业中，笔者还特意注意了代码注释的规范，努力写出赏心悦目的代码。

四、对象创建模式应用尝试

前面提到在每个类的构造方法中调用其value的simplify方法来规避冗余的存储结构嵌套，但是这种方法对扩展显然是很不友好的。

在学习了工厂方法模式之后，发现可以使用工厂来创建表达式项的对象，并将删除嵌套的过程放在工厂中，从而简化函数类的构造方法。代码如下（以构造正弦三角函数为例）：

public interface termFactory {
    public abstract Term create(Term val);
}

public class sineFactory implements termFactory {
    @Override
    public Term create(Term val) {
        Term value = val.simplify();
        return new Sine(value);
    }
}

这种方式将冗余嵌套删除过程提到了类构造函数之外，简化了类的构造逻辑，增强了扩展性，同时符合设计的“开闭原则”。