树状数组详解

树状数组

 

一、 引言

　　解题过程中，我们有时需要维护一个数组的前缀和S[i]=A[1]+A[2]+A[3]+A[4]+…+A[i]。

　　但是不难发现，如果我们修改了一个 A[i], S[i]、S[i+1]…S[n]都会发生变化。

　　可以说，每次修改 A[i]后，调整前缀和 S 在最坏的情况下会需要 O(n)的时间。

　　当 n 非常大时，程序会运行得非常慢。因此，这里我们引入“树状数组”，它的修改与求和都是 O(logn), 效率非常高。

 

二、 基本思想

　　根据任意正整数关于 2 的不重复次幂的唯一分解性质，若一个正整数 x 的二进制表示为 10101，

　　其中等于 1 的为是 0,2,4，则正整数 x 可以被“二进制分解”成 2^4+2^2+2^0。

　　进一步地，区间[1, x]可以分成 O(logx)个小区间：

　　　　· 长度为 2^4 的小区间[1, 2^4]

　　　　· 长度为 2^2 的小区间[2^4+1, 2^4+2^2]

　　　　· 长度为 2^0 的小区间[2^4+2^2+1, 2^4+2^2+2^0]

　　树状数组就是一种基于上述思想的数据结构，其基本用途是维护序列的前缀和。

　　对于区间[1, x], 树状数组将其分为 logx 个子区间，从而满足快速询问区间和。

 

三、 基本算法

　　由上文可知，这些子区间的共同特点是：

　　若区间结尾为 R,则区间长度就等于 R 的“二进制分解”下最小的 2 的次幂，我们设为 lowbit(R)。

　　对于给定的序列A,我们建立一个数组c,其中c[x]保存序列A的区间[x-lowbit(x)+1,x]中所有数的和。

　　树状数组叶子结点代表 A 数组 A[1]~A[8]

　

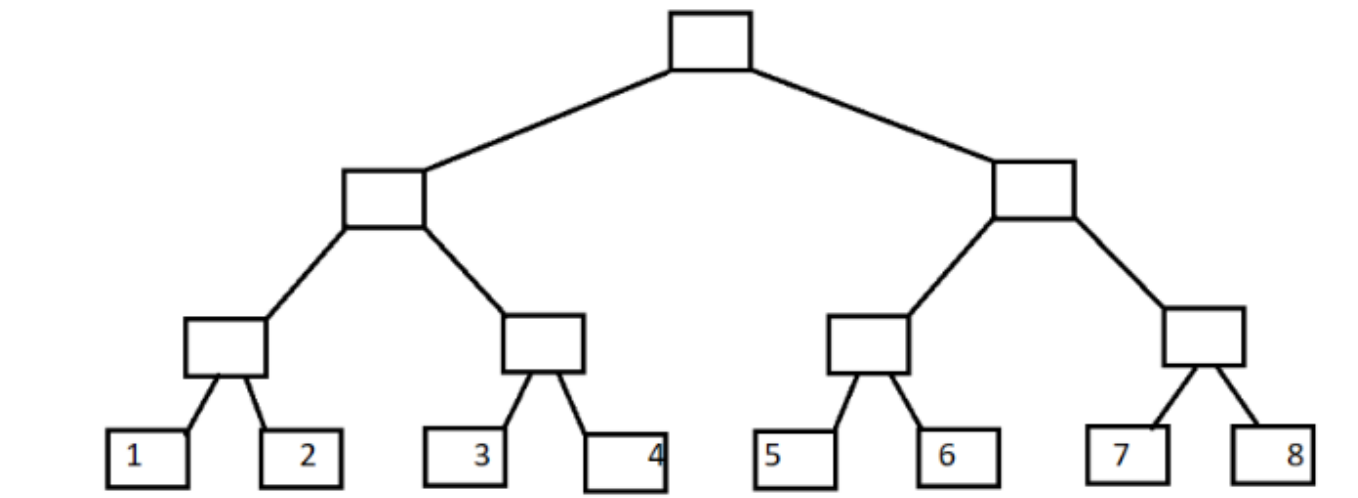
　　变形一下：

 　　现在定义每一列的顶端结点 C[]数组

　　C[i]代表子树的叶子结点的权值之和  // 这里以求和举例

　　如图可以知道：

　　C[1]=A[1];

　　C[2]=A[1]+A[2];

　　C[3]=A[3];

　　C[4]=A[1]+A[2]+A[3]+A[4];

　　C[5]=A[5];

　　C[6]=A[5]+A[6];

　　C[7]=A[7];

　　C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

 

　　下面观察如下图：

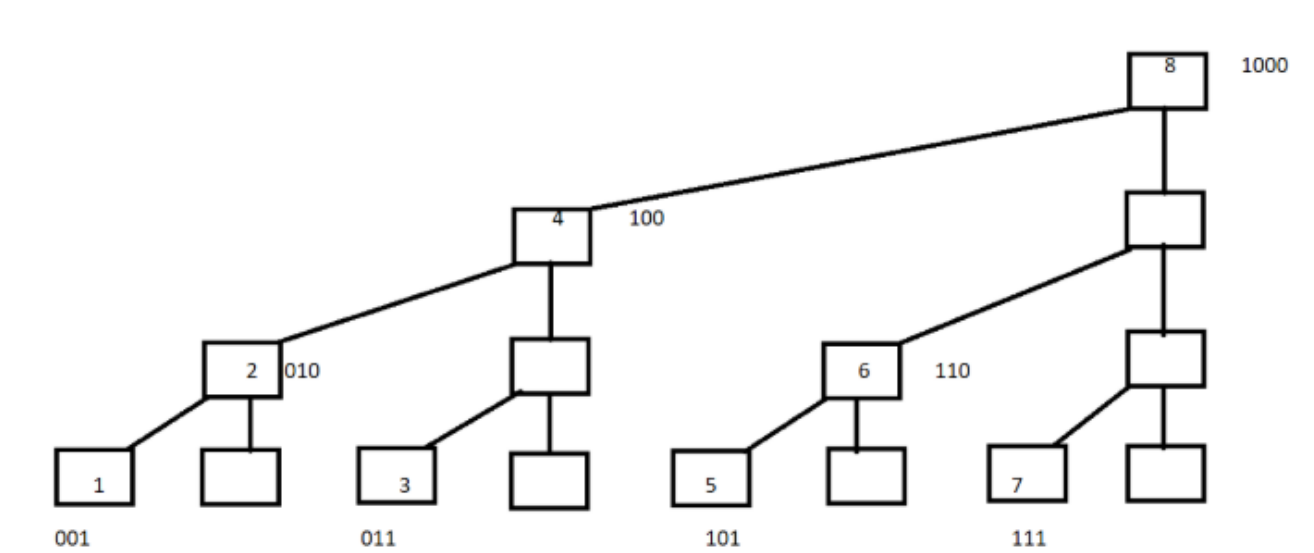
　　将C[]数组的结点序号转化为二进制：

　　1=(001)　　　　　　C[1]=A[1];

　　2=(010)　　　　　　C[2]=A[1]+A[2];

　　3=(011)　　　　　　C[3]=A[3];

　　4=(100)　　　　　　C[4]=A[1]+A[2]+A[3]+A[4];

　　5=(101)　　　　　　C[5]=A[5];

　　6=(110)　　　　　　C[6]=A[5]+A[6];

　　7=(111)　　　　　　C[7]=A[7];

　　8=(1000)　　　　　 C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]; 

　　对照式子可以发现 C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k 为 i 的二进制中从最

　　低位到高位连续零的长度）例如 i=8 时，k=3;

　　可以自行带入验证;

　　现在引入 lowbit(x)

　　lowbit(x) 其实就是取出 x 的最低位 1 换言之 lowbit(x)=2^k k 的含义与上面相同 理解一下

　　下面说代码

int lowbit(int t) { return t&(-t); }
//-t 代表 t 的负数，计算机中负数使用补码来表示
//例如 : // t=6（0110） 此时 k=1
//-t=-6=(1001+1)=(1010)
// t&(-t)=(0010)=2=2^1

 

　　C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i];

　　C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i]; 

 

四、区间查询

　　下面利用 C[i]数组，求 A 数组中前 i 项的和

　　举个例子 i=7;

　　sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ; 前 i 项和

　　C[4]=A[1]+A[2]+A[3]+A[4];　　C[6]=A[5]+A[6];　　C[7]=A[7];

　　可以推出: sum[7]=C[4]+C[6]+C[7];

　　序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];

　　再举个例子 i=5

　　sum[5]=A[1]+A[2]+A[3]+A[4]+A[5] ; 前 i 项和

　　C[4]=A[1]+A[2]+A[3]+A[4];　　C[5]=A[5];

　　可以推出: sum[5]=C[4]+C[5];

　　序号写为二进制: sum[(101)]=C[(100)]+C[(101)];

　　仔细观察二进制 树状数组其实就是二进制的应用

　　结合代码

int getsSum(int x)
{ 
    int ans=0; 
    for(int i=x;i>0;i-=lowbit(i)) 
        ans+=C[i]; 
    return ans;
}

　　对于 i=7 进行演示

　　7(111)　　　　　　　　　　　　　　ans+=C[7]

　　lowbit(7)=001　　7-lowbit(7)=6(110)   ans+=C[6]

　　lowbit(6)=010　　6-lowbit(6)=4(100)   ans+=C[4]

　　lowbit(4)=100　　4-lowbit(4)=0(000)

　　对于 i=5 进行演示

　　5(101)　　　　　　　　　　　　　　ans+=C[5]

　　lowbit(5)=001　　5-lowbit(5)=4(100)   ans+=C[4]

　　lowbit(4)=100　　4-lowbit(4)=0(000) 

 

五、单点更新

　　当我们修改 A[]数组中的某一个值时 应当如何更新 C[]数组呢？

　　回想一下区间查询的过程，再看一下上文中列出的图

　　结合代码分析

void update(int x,int y)
{ 
    for(int i=x;i<=n;i+=lowbit(i))
        C[i]+=y;
} 
//可以发现 更新过程是查询过程的逆过程 
//由叶子结点向上更新 C[]数组

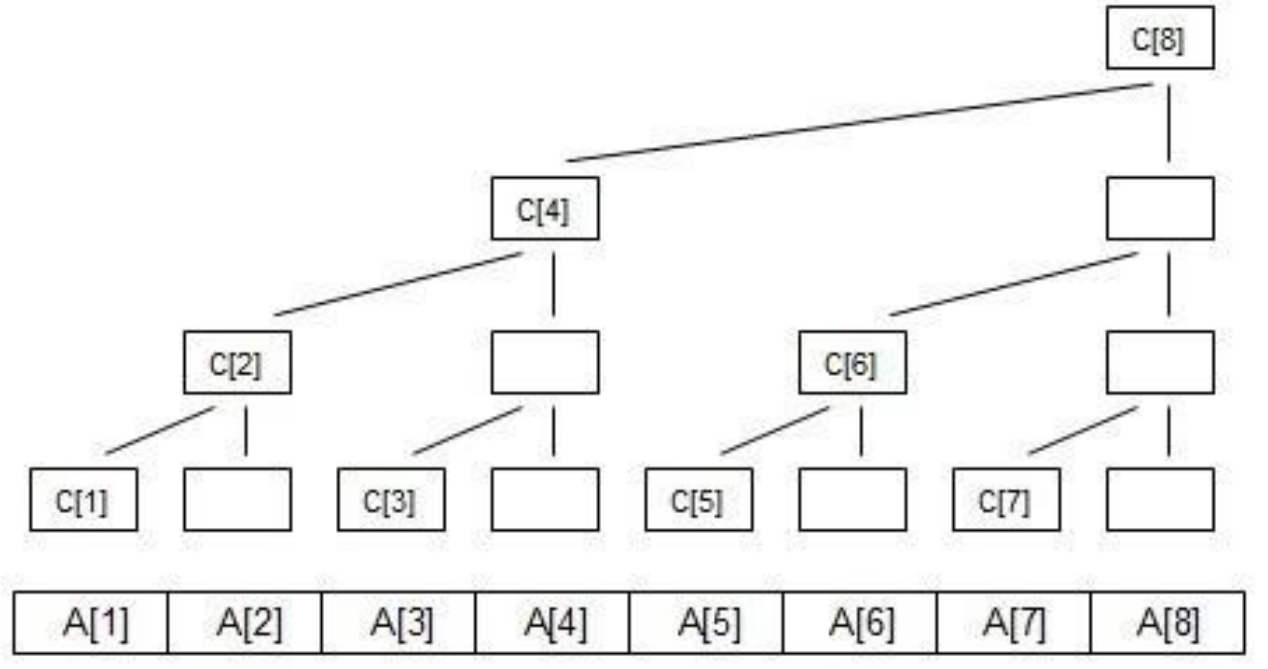
　　如图：

　　当更新 A[1]时 需要向上更新 C[1] ,C[2],C[4],C[8]

　　写为二进制 C[(001)],C[(010)],C[(100)],C[(1000)]

　　1(001)　　　　　　　　　　　　　　 C[1]+=A[1]

　　lowbit(1)=001　　1+lowbit(1)=2(010)   C[2]+=A[1]

　　lowbit(2)=010　　2+lowbit(2)=4(100)   C[4]+=A[1]

　　lowbit(4)=100　　4+lowbit(4)=8(1000) C[8]+=A[1] 

 

六、注意事项

　　要注意树状数组能处理的是下标为 1…n 的数组，绝对不能出现下标为 0 的情况。

　　因为lowbit(0)=0，这样会陷入死循环。 

 

七、例题练习

　　【例 1】#130. 树状数组 1 ：单点修改，区间查询

　　https://loj.ac/problem/130

　　【例 2】#10114. 「一本通 4.1 例 2」数星星 Stars

　　https://loj.ac/problem/10114

　　【例 3】#10115. 「一本通 4.1 例 3」校门外的树

　　https://loj.ac/problem/10115 

 

八、小结

　　在线性数据结构方面，树状数组与线段树异曲同工，

　　其优点在于算法时间复杂度低，并且可以大幅度降低程序调试难度，为选手节省时间。

　　但树状数组的使用条件要求更加严格。

　　它只能处理修改树状数组某一个点的数据，并不能有效处理修改一个区间的数据。

　　不过，对于某些题目，可以对其进行转化，将区间修改的操作转化为端点修改的操作。

　　总之，能用树状数组求解的题目，一定能用线段树求解，

　　但能用线段树求解的题目，不一定能用树状数组求解。