JS数据结构与算法
大纲:
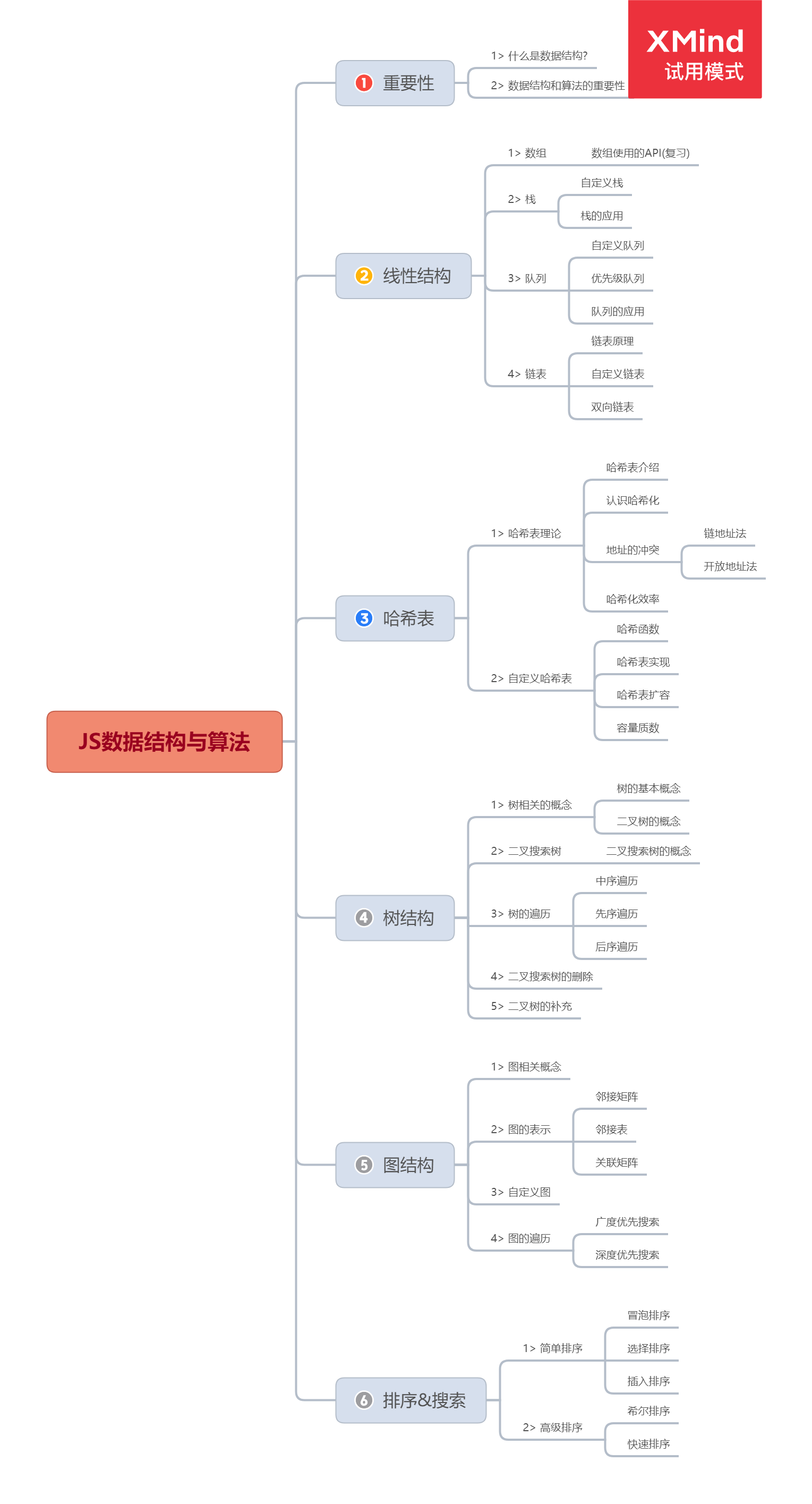
1、数据结构与算法
1.1、数据结构就是在计算机中存储和组织数据的方式。解决问题的效率和数组组织的方式有关:图书馆的书摆在正确的位置我才好找
1.2、算法:一个有限的指令集,每条指令的描述不依赖语言;可能会接受输入;产生输出;一定会在有限的步骤后停止
2、数组:插入、删除慢:查找:下标快;内容慢
常用API:join、reverse、concat、pop、push、shift、unshift、splice、slice、filter、map、forEach、every、some、sort、
reduce / reduceRight、toString / toLocaleString、indexOf / astIndexOf
3、栈:后进先出 LIFO。基于数组或链表;插入快,查找慢
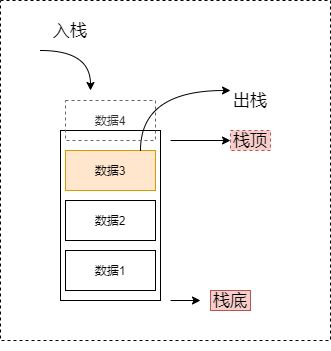
常见的操作(自定义封装):push、pop、peek返回栈顶、isEmpty、size、toString字符串全输出,等
4、队列:先进先出FIFO。基于数组或链表
只允许表前front出,表后rear进
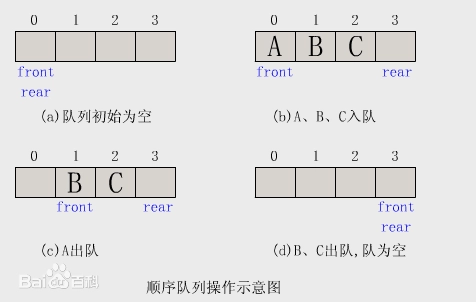
常见的操作(自定义封装):enqueue尾插、dequeue头删、front返回头、isEmpty、size、toString
4.1:优先级队列:插队。考虑新插入的元素与已有元素的优先级,从而确定插入位置
需要注意的点:1、每个元素不再只是一个数据,而是要包含数据的优先级;2、根据优先级将数据放入正确的位置
5、链表:本身节点与指向下一元素的引用(指针)
相对于数组的优点:不必连续,实现内存动态管理;创建时不必确定大小,可无限延伸;插入和删除的时候O(1)
相对于数组的缺点:访问任何一个元素时都要从头访问,无法通过下标直接访问
5.1:单向链表:只能从头遍历到尾或者从尾遍历到头(一般从头到尾)也就是链表相连的过程是单向的。
单向链表有一个比较明显的缺点:可以轻松的到达下一个节点,但是回到前一个节点很难.
常见操作:append尾部插入、insert指定位置插入、get指定位置元素、indexOf查找某一元素、update修改某一位置元素、removeAt删除指定位置元素、remove删除某一元素、isEmpty、size、toString

5.2:双向链表:既可以从头遍历到尾,又可以从尾遍历到头,也就是链表相连的过程是双向的。一个节点既有向前连接的引用,也有一个向后连接的引用。
双向链表缺点:每次在插入或删除某个节点时,需要处理四个节点的引用,而不是两个。也就是实现起来要困难一些,并且相对于单向链表,必然占用内存空间更大一些

常见操作:append尾部插入、insert指定位置插入、get指定位置元素、indexOf查找某一元素、update修改某一位置元素、removeAt删除指定位置元素、remove删除某一元素、isEmpty、size、toString、forwardString正序输出、reverseString逆序输出
哈希前序知识:集合与字典(Map映射):
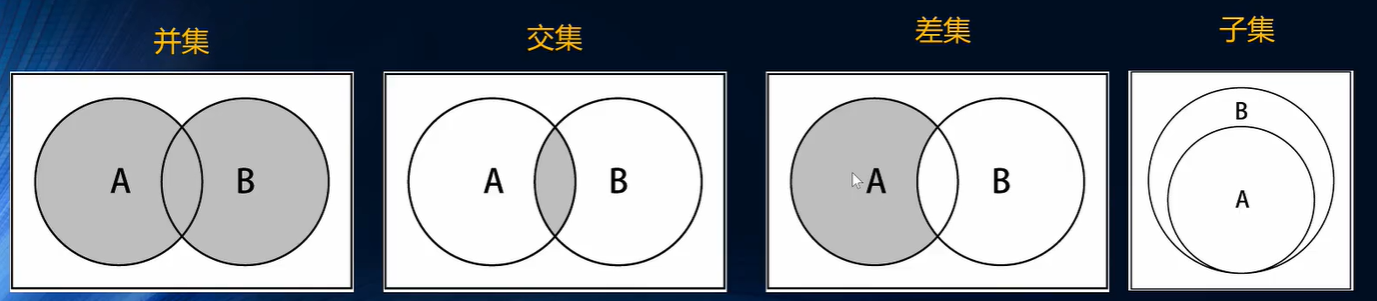
集合:无序、不能重复
常见操作:并集、交集、差集、子集:A是否全包含于B
字典(Map映射):一一对应、键值对、无序。Key不可重复,value可重复
6、哈希表:基于数组;但是有更快的插入-删除-查找:O(1);比树快,但是空间利用率不高。
基于数组,针对下标值的一个变换(哈希函数),得到HashCode

6.1:哈希函数:将单词转换成大数字,大数字进行哈希化的代码实现就是哈希函数
6.2:哈希化:大数字转换成数组范围内下标的过程
6.3:哈希表:最终将数据插入到这个数组,整个结构封装,这个结构就是哈希表
6.4:冲突:哈希化后存在两个相同的值,虽然可能比较小,但是还是有可能发生。
解决:6.4.1:链地址法
6.4.2:开放地址法
链地址法(拉链法):在哈希表每一个单元中设置链表(数组),某个数据项对的关键字还是像通常一样映射到哈希表的单元中,而数据项本身插入到单元的链表中
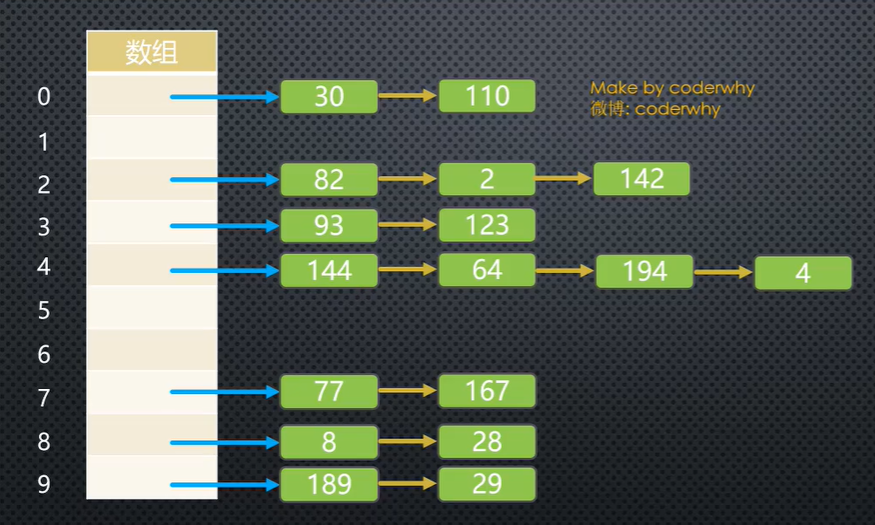
关于选择数组还是链表:由于哈希化后查找基本是用index线性查找,效率差不多;但是有些情况下,新插入的数据会被考虑到取出来的可能性大,所以可能会插入到头部,这时候选择链表比较好。
开放地址法:寻找空白的单元格添加重复的数据

寻找空白单元格的三个方法:
线性探测:线性查找。
约定:线性插入配合线性查找,通过线性插入的元素,需要用线性查找来查询。如果删除该元素,不能把这个元素的位置置为null而要为-1,因为线性查找碰到null就会停止,当看到-1的时候会继续往下查询。
缺陷:聚集。一连串填充单元成为聚集,如21、22、23插入后占据1、2和3,为了放置一个数据而探测多次,影响性能。
二次探测:基于线性探测,对步长进行优化:index+1^2、index+2^2.....也称为平方探测
缺陷:21-31-51-101都插入到1,但是这样会对1这个类的平方步长造成聚集(当然,相对于线性来说可能性小)
再哈希法:不同关键字使用不同的步长,如21-31-51-101,给每个都取不同步长防止聚集。
步骤:关键字用另一个哈希函数再哈希化,使用这次的结果作为步长。
二次哈希需要的特点:和第一个哈希函数不同,要是相同那还是原来的位置;不能输出0,不然就死循环了
stepSize = constant -(key % constant) constant为质数,且小于数组容量
6.5:哈希化的效率:如果没冲突,自然效率高;如果冲突,存取时间依赖后来的探测长度。
平均探测长度和平均存取时间取决于填装因子,其越大,长度越长。一般大于0.75就要扩容,小于0.25就缩容
填装因子 = 已包含总数据 / 哈希表长度
开放地址法填装因子最大为1(全填充);链地址法可超过1(拉链)
一般来说,链地址法用的多,性能不会急剧下降,Java的HashMap和别的,基本都是链地址法
少用乘除,快速获得hashCode:比如多项式用秦九韶算法优化;数据均匀分布;常数部分多用质数。
6.6:一般的hash表结构:[ [ [k,v],[k,v],[k,v] ] , [ [k,v],[k,v],[k,v] ] ],大数组哈希化,包含多个桶,每个桶拉链,每个链又用一个数组保存[key,value]
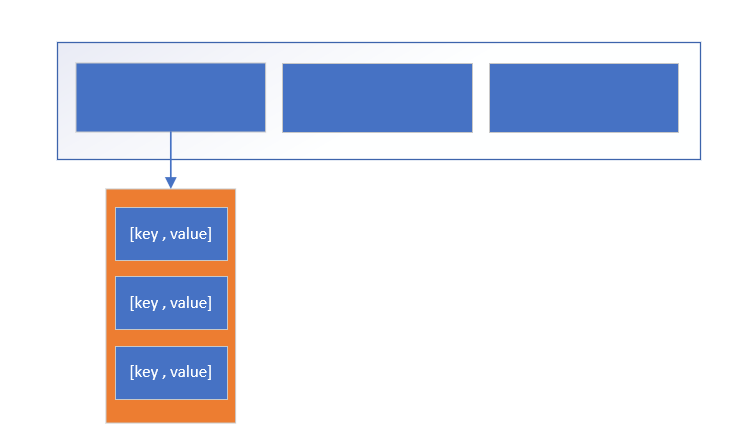
6.7:哈希表的扩容:数据增多造成的桶过长,效率降低。
扩容一般扩容成一个质数,乘二并寻找最接近的质数;扩容时limit改变了,所以要重新装载全部数据;
一般填装因子大于0.75就扩容,小于0.25缩容。
6.8:质数的判断:只能被自己和1除的数。
//低效代码 function isPrime(num) { for (var i = 2; i < num; i++) { if (num % i == 0) { return false } } return true } //有些不需要相除判断的 function isPrime(num) { // 1.获取平方根 var temp = parseInt(Math.sqrt(num)) // 2.循环判断 for (var i = 2; i <= temp; i++) { if (num % i == 0) { return false } } return true }
//还有其他如孪生素数等方法
7、树:空间利用率比哈希表高,查找效率比数组和链表高
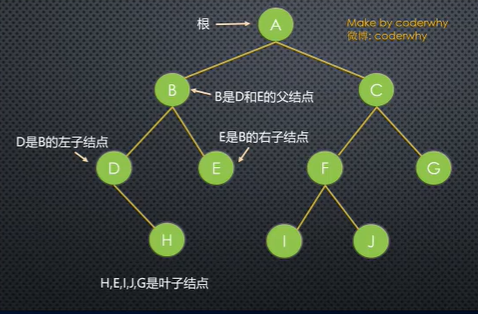
7.1:树:n(n>=0)个节点构成的有限集合。n=0称为空树;n>0为非空树。
7.2:非空树:
- 根,r表示;
- 其余节点可以分为m(m>0)个不相交的有限集T1、T2...Tm,每个集合本身又是一棵树,称为原来大树的“子树”;
- 结点(Node):表示树中的数据元素,由数据项和数据元素之间的关系组成。
- 结点的度(Degree of Node):结点所拥有的子树的个数,
- 树的度(Degree of Tree):树中各结点度的最大值。
- 叶子结点(Leaf Node):度为0的结点,也叫终端结点。
- 分支结点(Branch Node):度不为0的结点,也叫非终端结点或内部结点。
- 孩子(Child):结点子树的根。
- 双亲(Parent):结点的上层结点叫该结点的双亲。
- 祖先(Ancestor):从根到该结点所经分支上的所有结点。
- 子孙(Descendant):以某结点为根的子树中的任一结点。
- 兄弟(Brother):同一双亲的孩子。
- 结点的层次(Level of Node):从根结点到树中某结点所经路径上的分支数称为该结点的层次。根结点的层次规定为1,其余结点的层次等于其双亲结点的层次加1。
- 堂兄弟(Sibling):同一层的双亲不同的结点。
- 树的深度(Depth of Tree):树中结点的最大层次数。
- 无序树(Unordered Tree):树中任意一个结点的各孩子结点之间的次序构成无关紧要的树。通常树指无序树。
- 有序树(Ordered Tree):树中任意一个结点的各孩子结点有严格排列次序的树。二叉树是有序树,因为二叉树中每个孩子结点都确切定义为是该结点的左孩子结点还是右孩子结点。
- 森林(Forest):m(m≥0)棵树的集合。自然界中的树和森林的概念差别很大,但在数据结构中树和森林的概念差别很小。从定义可知,一棵树有根结点和m个子树构成,若把树的根结点删除,则树变成了包含m棵树的森林。当然,根据定义,一棵树也可以称为森林。
7.3:表示方式:
7.3.1:普通表示:当数据增加时,不好表示
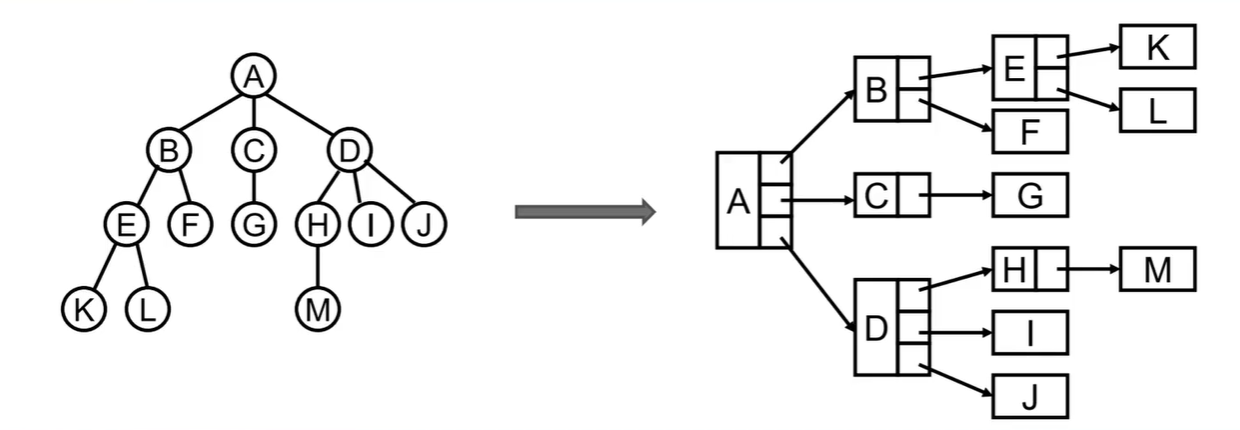
7.3.2:儿子兄弟表示法:左表示子,右表示兄

引出二叉树:
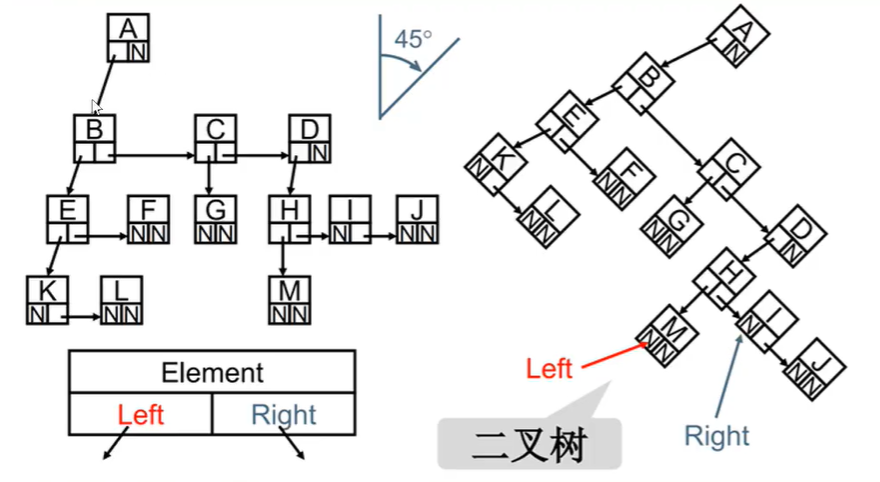
7.4:二叉树:树中每个节点最多只能有两个子节点。所有树的本质其实都是二叉树
7.4.1、定义:二叉树可以为空(没有节点);若不为空,则它是由根节点和左子树TL和右子树TR的两个不相交的二叉树组成
7.4.2、形态:
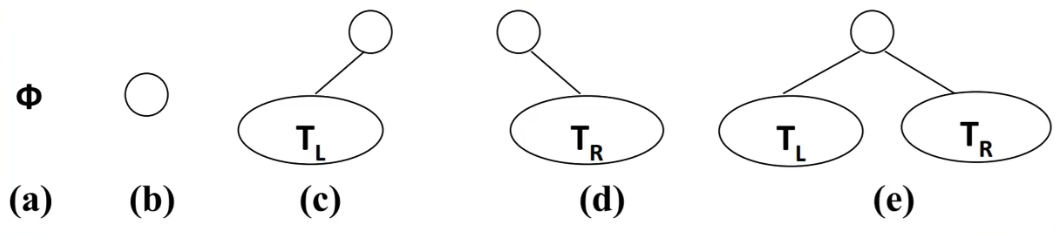
7.4.3、特性:1、二叉树第 i 层最大节点数:2^(i-1), i>=1
2、深度为k的二叉树有最大节点总数:2^k-1, k>=1
3、对任何非空二叉树T,n0表示叶节点的个数、n2是度为2的非叶节点个数,则n0=n2+1
7.4.4、类型
完美二叉树(满二叉树):除了最下层叶子,其他都有2个子节点
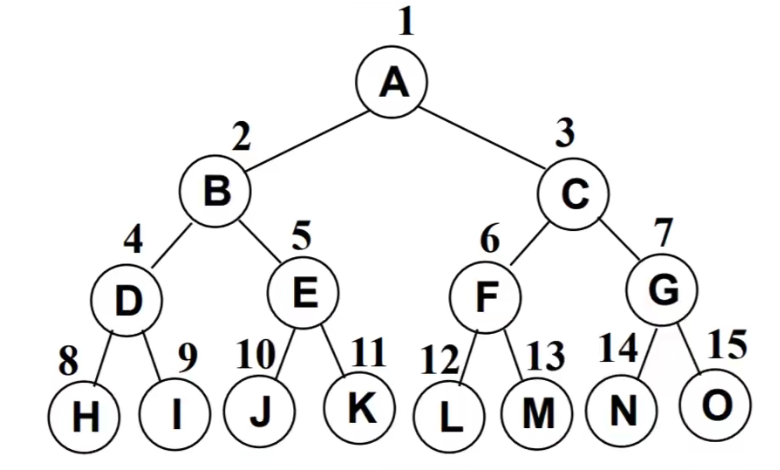
完全二叉树:除最后一层外,其他各层节点都达到最大个数;最后一层节点从左往右连续存在,只缺右侧若干节点。完全二叉树包含完美二叉树
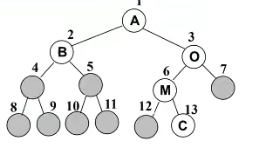
7.4.5:二叉树存储:常见为数组和链表
数组:一般用完全二叉树,非完全二叉树会造成空间浪费;
链表:二叉树最常用的存储方法。每个节点封装一个Node,Node包含左引用和右引用。
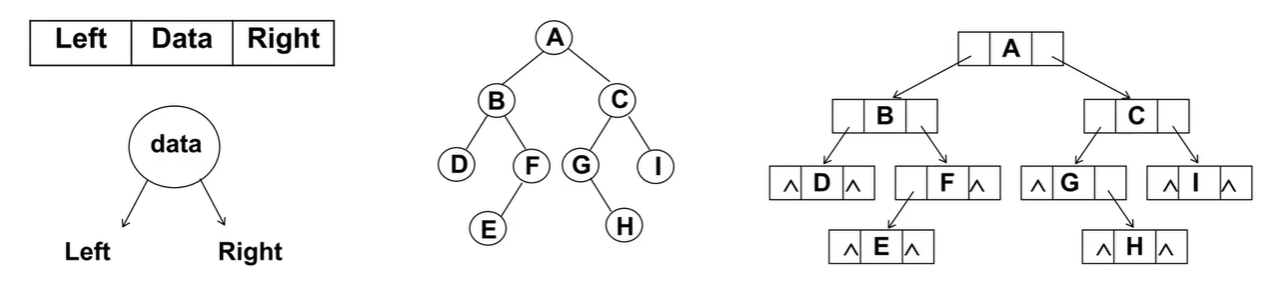
7.4.6:二叉搜索树(二叉排序树,二叉查找树):可以为空
非空性质:非空左子树的键值小于其根节点的键值;非空右子树的键值大于其根节点的键值;左、右树本身也是二叉搜索树。
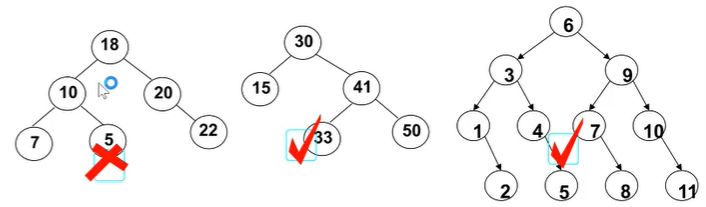
所以,在二叉搜索树中,大值基本在左边,小值在右边。所以其查找效率非常高。利用了二分查找的思想
常见操作:
递归操作(这里要理解执行上下文),如递归判断再插入等;
遍历,先序遍历、中序遍历、后续遍历和程序遍历(这个用得比较少)
A、先序遍历:1、根节点;2、先序遍历左;3、先序遍历右
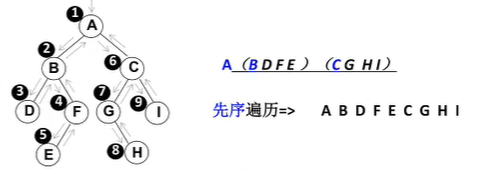
B、中序遍历:1、中序遍历左;2、根;3中序遍历右
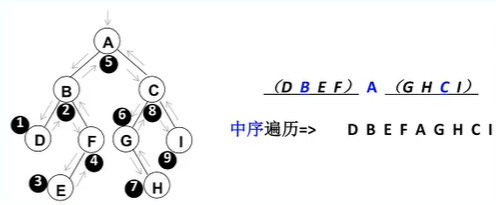
C、后序遍历:1、后序遍历左;2、后序遍历右;3根
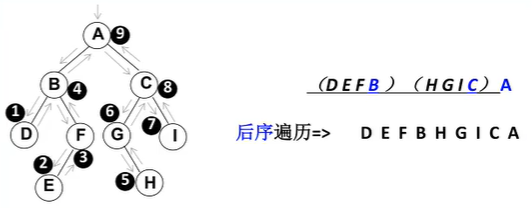
最大值max、最小值min,往最右和最左找就行
搜索,其实也和插入差不多,二分找
删除,难点。需要考虑的较多:
情况1:删除的结点为叶子结点,父节点的left或者right置空即可(这里还要先判断是否为根节点,根节点没有parent);
情况2:删除的结点只有一个子节点,让其父节点指向子节点即可;
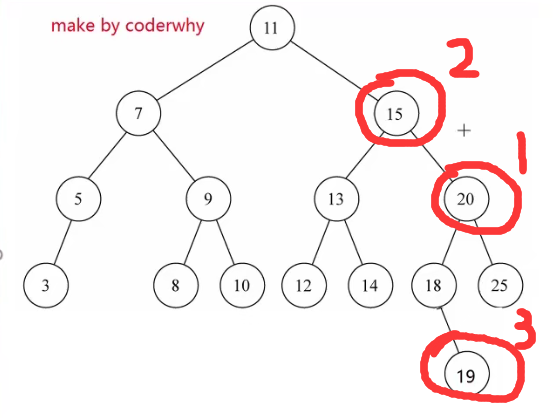
BinarySerachTree.prototype.getSuccssor = function (delNode) { let parentNode = delNode let currentNode = delNode.right //两种情况 //1、当删除节点为叶子节点上一个,则父节点,也就是要删除的节点的右指向null if (currentNode.left == null) { //这里要判断子节点的右是否为空,若不为空,则父的右指向子的右 parentNode.right = currentNode.right != null ? currentNode.right : null } else { //2、当删除节点不为叶子节点上一个,则父节点,找到右树最小叶子,叶子的父节点左指向null while (currentNode.left !== null) { parentNode = currentNode currentNode = currentNode.left } //这里还有一种情况要考虑,当后继还有右节点时,父节点的left应该指向当前的right parentNode.left = currentNode.right != null ? currentNode.right : null } return currentNode.key } }
二叉搜索树可以快速查找,快速插入和删除项。但是如果插入的是有序数据,会造成链状插入,过大的深度会影响性能。
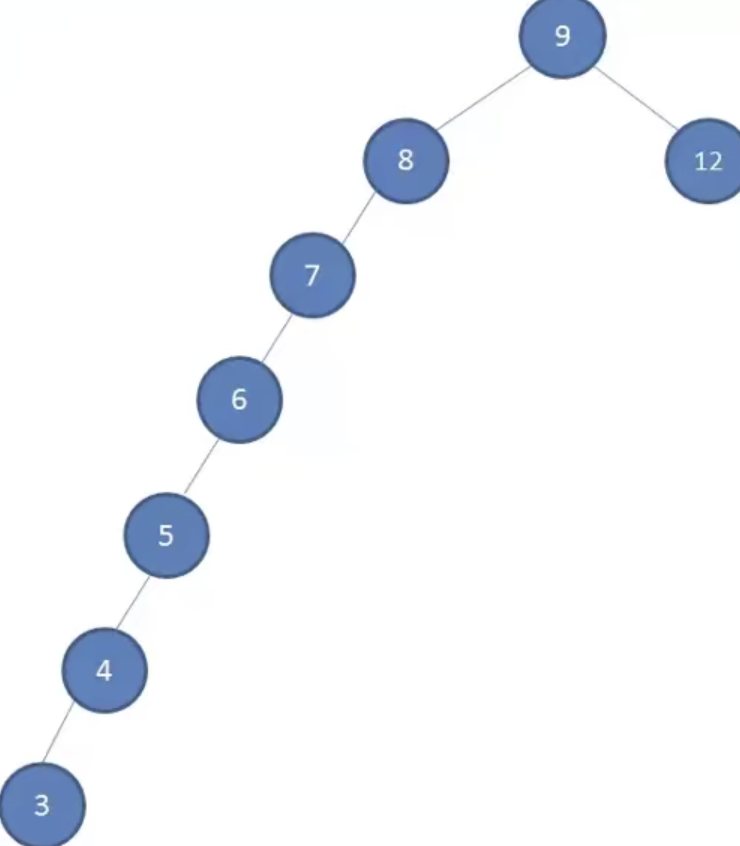
该树可称为非平衡树 O(N),好的二叉树应该是分布均匀的平衡树 O(logn)
7.4.7:引申出 平衡二叉树:树种节点左子孙节点的个数尽量与右子孙节点的个数相同
常见的平衡树:AVL树、红黑树
7.4.8:红黑树:符合二叉树的特性,且有额外特性(规则):
1、节点是红色和黑色
2、根节点是黑色
3、每个叶子节点都是黑色空节点NIL
4、每个红色节点的两个子节点都是黑色NIL(即不会有两个连续的红色节点)
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
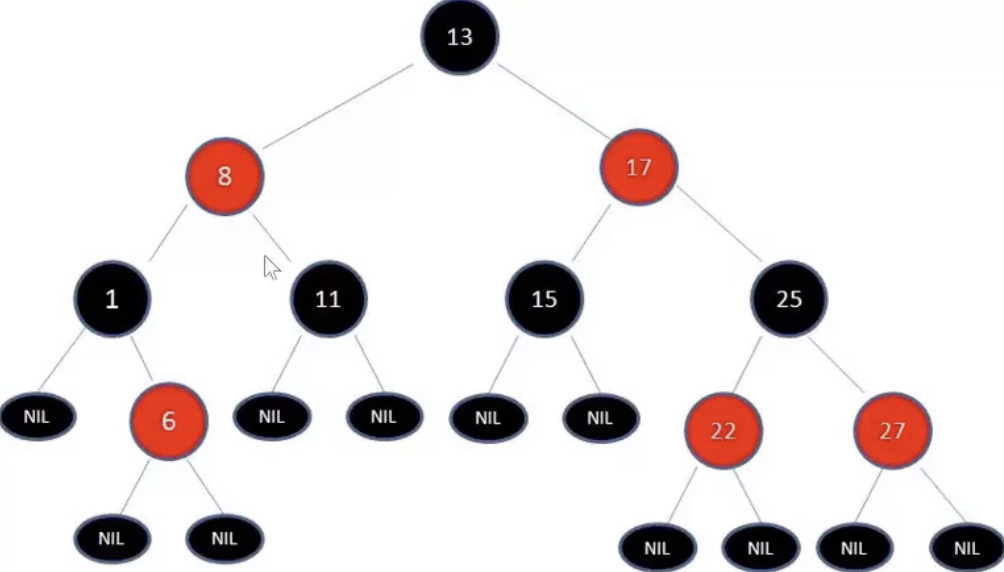
7.4.8.1:红黑树的相对平衡:从根到叶子的最长可能路径,不会超过最短可能路径的两倍长
当插入新节点时,有可能树不平衡,需要调整变换:变色、左旋转、右旋转
变色:尝试把红转黑,或者黑转红;
首先,需要知道插入的新的节点通常都是红色节点。
因为在插入节点为红色的时候,有可能插入一次是不违反红黑树任何规则的;而插入黑色节点,必然会导致有一条路径上多了黑色节点,这是很难调整的.
红色节点可能导致出现红红相连的情况,但是这种情况可以通过颜色调换和旋转来调整
旋转:左旋转(逆时针)
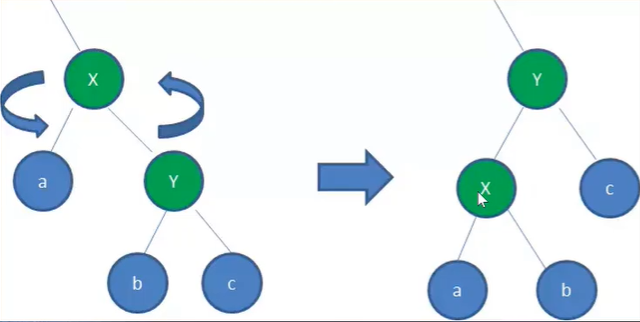
右旋转(顺时针)
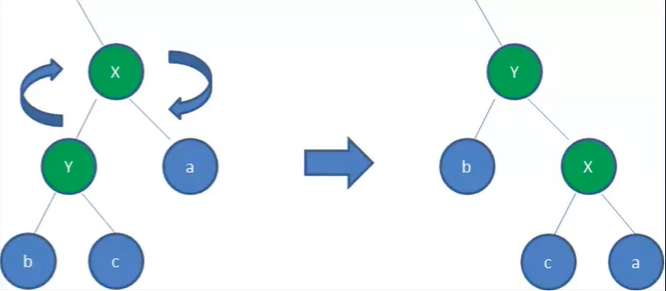
7.4.8.2:操作:
1、插入:假设,当前节点为N、父节点为P、祖父节点为G、父亲的兄弟,即伯父节点为U
情况一:新节点位于根,没有父节点:红转黑即可
情况二:新节点父节点为黑:直接插入红新节点即可
情况三:P为红,U为红,G为黑:P、G、U变色即可,然后G为根,G再变黑;但可能G上一级的节点本来是红色的,就违反第四规则了,可以递归处理。
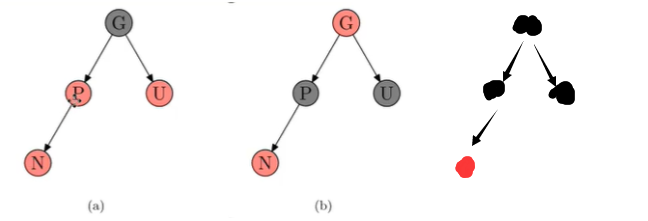
情况四:P红、G和U黑,且右兄弟黑:P黑、G红,且进行PGU右旋转(图是先旋转,再变色)
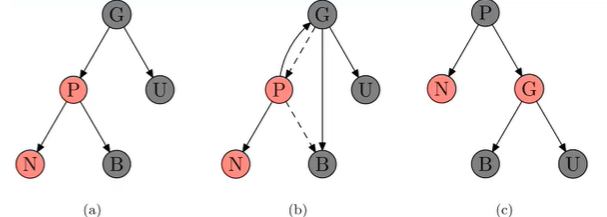
情况五:P红、G和U黑,且左兄弟黑:PBN左旋转,然后把P作为新节点:N黑G红,GNU右旋转
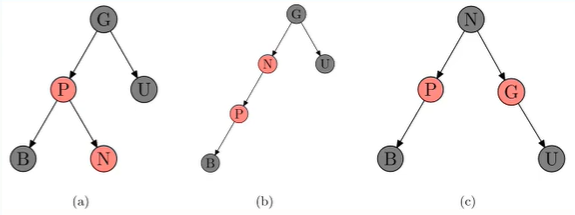
注意:以上所有操作都只在NPGU四个点进行,其他点不进行变色或旋转
2、删除(考虑二叉树的删除):
8、图:与树类似;树是图的一种;研究顶点和边组成的图形的数学理论和方法;主要研究事物之间的关系,顶点为事物,边为关系。
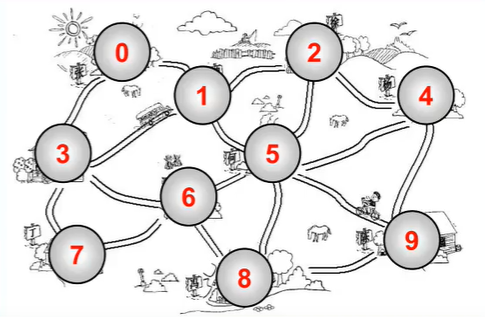
顶点Vertex,V表示顶点的集合;边Edge,E表示边的集合。边是顶点的连线,边可以有向也可以无向。运筹学里的弗洛伊德算法、狄克斯特拉算法解决方式
8.1:图的相关术语:
顶点:即图中的一个个节点
边:顶点和顶点之间的连线
相邻顶点:一条边连接在一起的顶点
度:一个顶点的相邻顶点的数量
路径:顶点的连续序列,如上图的0-1-5-9。分为简单路径(起点终点不同,且无重复顶点)和回路(一个闭环,起点终点为同一个顶点)两种。
无向图、有向图:有无方向
无权图、带权图:有无权重:距离,价格等
8.2:图的表示:顶点和边
邻接矩阵:每个节点和一个正数相关联,自己到自己的自回路用0表示,若要改成有权图,1换成权重大小即可。
缺点:如果是一个稀疏图,会存在大量的0,浪费空间
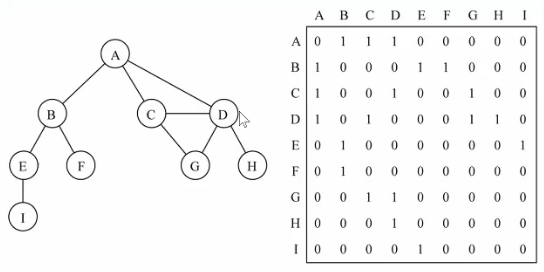
邻接表:由图中每个顶点和顶点相邻的顶点列表组成。数组/链表/字典(哈希表)表示都可以
缺点:出度(指向别人的数量)计算方便;入度(指向自己的数量)麻烦,需要设计逆邻接表,但是入度其实用得不多

8.3:操作:添加顶点(数组等)、添加边(字典等)、toString、遍历
遍历:广度优先搜索(Breadth-first search,BFS)海王、深度优先搜索(Deep-first search,DFS)专情
明确第一个被访问的顶点,树默认从根,图不一样。
广度优先搜索:从第一个顶点开始遍历图,访问所有相邻点,先宽后深的访问顶点。一般用队列来完成比较简单
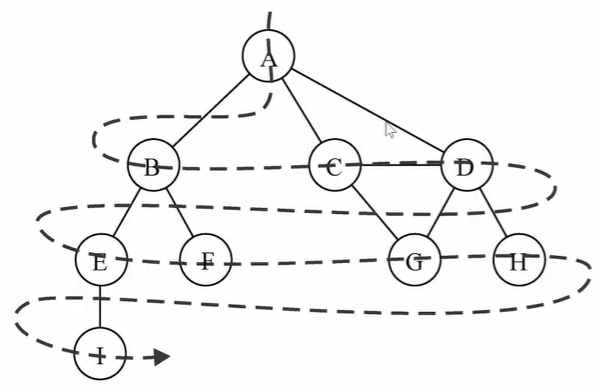
//广度优先,队列
//传入第一个被访问的点 Graph.prototype.breadthSearch = function (initV) { //这里可以使用一个颜色数组串,别的也可以,用于判断顶点是否被访问过,这样就不用重复访问 //白色:未访问未探测,灰色:访问未探测,黑色:探测 let colors = this.initializeColor() //创建一个空队列 let queue = new Queue() //将第一个V加入队列,并置灰 queue.enqueue(initV) //如果队列非空,则循环 while (!queue.isEmpty()) { //将V取出 let v = queue.dequeue() //V标注为灰色 colors[v] = 'gary' //V的未被访问过的邻接点(白色),加入队列 let vs = this.edges.get(v) //遍历顶点,加入队列 for (let i = 0; i < vs.length; i++) { let el = vs[i] //根据颜色判断是否探测过,防止重复添加 if (colors[el] == 'white') { colors[el] = 'gray' queue.enqueue(el) } } //V标志为黑 colors[v] == 'black' } }
深度优先搜索:顶点开始遍历图,沿着路径直到最后一个,然后原路返回探索新路径,和树的先序遍历类似。
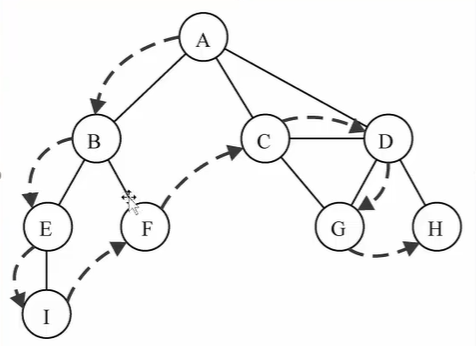
//深度优先,递归 Graph.prototype.deepSearch = function (initV) { let colors = this.initializeColor() //顶点递归访问 this.dfsAccess(initV, colors, handler) } Graph.prototype.dfsAccess = function (v, colors, handler) { colors[v] = 'gray' //访问v相连顶点 let vs = this.edges.get(v) for (let i = 0; i < vs.length; i++) { let el = vs[i] //根据颜色判断是否探测过,防止重复添加 if (colors[el] == 'white') { this.dfsAccess(el, colors) } } colors[v] == 'black' }
大O表示:粗略度量计算机算法的效率
表示方法:算法的速度会如何跟随数据量的变化而变化。
常见表示函数:
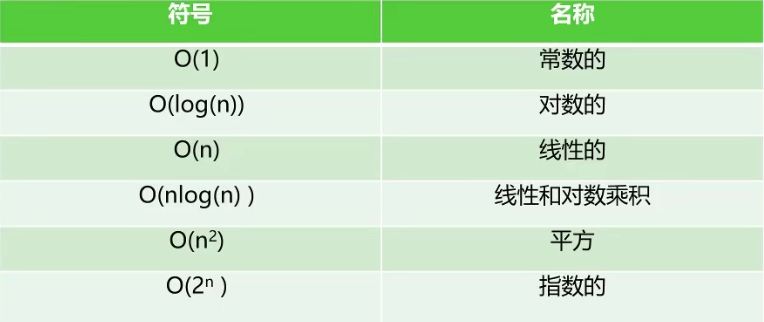
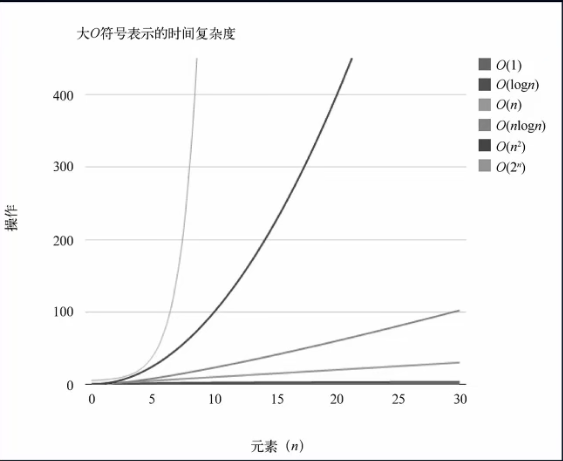
排序算法:
1、简单排序:冒泡、选择、插入
2、高级排序:希尔、快速、归并、技术、基数、堆、桶


 浙公网安备 33010602011771号
浙公网安备 33010602011771号