HDU - 1560 DNA sequence IDA*迭代式深搜

题目

DNA sequence

*Time Limit: 15000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7590 Accepted Submission(s): 3354
*

Problem Description

The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.

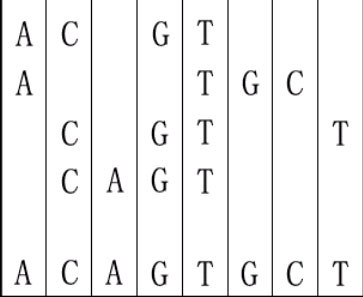
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

Input

The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

Output

For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

Sample Input

1
4
ACGT
ATGC
CGTT
CAGT

Sample Output

8

Author

LL

Source

HDU 2006-12 Programming Contest

思路 （IDA* 迭代式深搜）

​ 迭代式深搜的目的是为了减少空间上的浪费，众所周知BFS队列会提升空间复杂度, IDA*是限制深度

的深搜，对每个深度进行枚举，若达到上限深度则停止。

​ 对于本题，最大深度是所有DNA序列之和，最小深度是从所有字符中最大的开始，然后进行dfs，若当前匹配需要的最小深度大于当前的限制深度，那么我们直接return，当前匹配的最小深度可以通过计算每个串的匹配位置来得到，这样我们就可以类似于BFS的进行每一层的搜索

Code

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 10;

string ex = "ATCG";


// pos数组负责记录当前串的匹配位置
int n, deep, pos[N], ans;

vector<string> a;

string now;

bool flag;


int cal(int pos[]) {
	int mx = 0;
	for (int i = 0; i < a.size(); i ++) {
		int len = (int) a[i].length();
    // 最小所需深度=max(当前串的匹配位置减去其长度，即还所需匹配的字符)
		mx = max(mx, len - pos[i]);
	}
	return mx;
}

void dfs(int u, int pos[]) {

	if (u > deep) return;
	// cout << u << endl;
	if (flag) return;
	
  // 计算所需最小深度
	int mx = cal(pos);
  
	// 若当前需要的最小深度大于当前深度或需要的深度为0，则找到答案
	if (u + mx > deep || !mx) {
		if (!mx) ans = u;
		return;
	}
  
	// t为更新后的pos
	int t[N];
	
  // 枚举ACTG进行DFS
	for (int i = 0; i <= 3; i ++) {	
		bool check = false;
		for (int j = 0; j < a.size(); j ++) {
			t[j] = pos[j];
      // 若当前的pos位小于当前匹配串的大小，并且和当前串所对应字符相同
			if (pos[j] < a[j].size() && ex[i] == a[j][pos[j]]) {
				t[j] = pos[j] + 1;
				check = true;
			}
		}
		if (check) dfs(u + 1, t);
		if (flag) return;
	}
}


int main() {
	string t;
	int _;
	cin >> _;
	while (_ --) {
		deep = 0;
		a.clear();
		cin >> n;
		for (int i = 0; i < n; i ++) {
			cin >> t;
			a.push_back(t);
      // 记录最小所需深度
			deep = max(deep, (int) t.size());
		}

		ans = -1;
	
    // ida*枚举每个深度进行DFS，相当于DFS版本的宽搜
		while(true) {
			memset(pos, 0, sizeof pos);
			dfs(0, pos);
			if (ans != -1) {
				cout << ans << endl;
				break;
			}
			deep ++;
		}
	}
}