POJ3895

Cycles of Lanes

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2051		Accepted: 752

Description

Each of the M lanes of the Park of Polytechnic University of Bucharest connects two of the N crossroads of the park (labeled from 1 to N). There is no pair of crossroads connected by more than one lane and it is possible to pass from each crossroad to each other crossroad by a path composed of one or more lanes. A cycle of lanes is simple when passes through each of its crossroads exactly once.
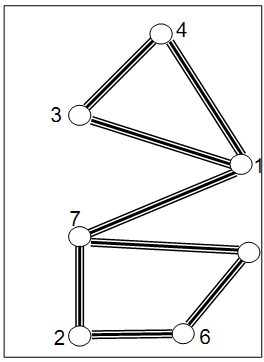
The administration of the University would like to put on the lanes pictures of the winners of Regional Collegiate Programming Contest in such way that the pictures of winners from the same university to be on the lanes of a same simple cycle. That is why the administration would like to assign the longest simple cycles of lanes to most successful universities. The problem is to find the longest cycles? Fortunately, it happens that each lane of the park is participating in no more than one simple cycle (see the Figure).

Input

On the first line of the input file the number T of the test cases will be given. Each test case starts with a line with the positive integers N and M, separated by interval (4 <= N <= 4444). Each of the next M lines of the test case contains the labels of one of the pairs of crossroads connected by a lane.

Output

For each of the test cases, on a single line of the output, print the length of a maximal simple cycle.

Sample Input

1 
7 8 
3 4 
1 4 
1 3 
7 1 
2 7 
7 5 
5 6 
6 2

Sample Output

4

package pro.proclass.chaopengfan;

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class POJ3895 {
    private static int N, M, num, ans, index;
    private static int[] low, dfn, parent, container;
    private static boolean[] visit;
    private static ArrayList<Integer>[] arr;
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int T = Integer.parseInt(st.nextToken());

        for (int t = 1; t <= T; t++) {
            st = new StringTokenizer(br.readLine());
            N = Integer.parseInt(st.nextToken());
            M = Integer.parseInt(st.nextToken());
//            data = new int[N+1][N+1];
            low = new int[N+1];
            dfn = new int[N+1];
            parent = new int[N+1];
            container = new int[N+1];
            visit = new boolean[N+1];
            arr = new ArrayList[N+1];
            num = 0;
            ans = 0;
            index = 0;

            for (int i = 0; i <= N; i++) {
                arr[i] = new ArrayList();
            }

            for (int i = 0; i < M; i++) {
                st = new StringTokenizer(br.readLine());
                int a = Integer.parseInt(st.nextToken());
                int b = Integer.parseInt(st.nextToken());

                arr[a].add(b);
                arr[b].add(a);
            }
            visit[1] = true;
            parent[1] = 1;

            for (int i = 1; i <= N; i++) {
                if(dfn[i] == 0)
                tarjan(i);
            }

            System.out.println(ans);
        }
    }

    private static void tarjan(int x) {
        low[x] = dfn[x] = ++num;
        container[++index] = x;
        for (int i = 0; i < arr[x].size(); i++) {
            int n = arr[x].get(i);
            if(parent[x] == n) continue;// 避免走到底，回溯走向自己亲父节点导致错误

            if(dfn[n] == 0) {
                visit[n] = true;
                parent[n] = x;
                int tem = num;
                tarjan(n);
                num = tem; // 找到一个环之后重新计数编号
                low[x] = Math.min(low[n], low[x]);
            }
            else if(visit[n]) {
                low[x] = Math.min(dfn[n], low[x]);
                ans = Math.max(ans, dfn[x] - dfn[n] + 1);
            }
        }

        if(low[x] == dfn[x]) {
            while (true) {
                int cur = container[index];
                index--;
                visit[cur] = false;
                if(cur == x) break;
            }
        }
    }
}

 

这里简单方法

package com.Vjudge;

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

import static java.lang.Integer.parseInt;

//A - 图论找最大环
//POJ 3895
public class A {

    static StringTokenizer st;
    static int N, M, u, v, cnt, ans;
    static Edge[] edges;
    static int[] head, dp;
    static boolean[] visited;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = parseInt(br.readLine());
        for (int i = 0; i < T; i++) {
            st = new StringTokenizer(br.readLine());
            N = parseInt(st.nextToken());
            M = parseInt(st.nextToken());
            initD();

            for (int j = 0; j < M; j++) {
                st = new StringTokenizer(br.readLine());
                u = parseInt(st.nextToken());
                v = parseInt(st.nextToken());
                addEdge(u, v);
                addEdge(v, u);
            }
            for (int k = 1; k <= N; k++) {
                if (!visited[k]) {
                    dfs(k, 1);
                }
            }
            if (ans <= 2) {
                System.out.println(0);
            } else {
                System.out.println(ans);
            }
        }
    }

    private static void initD() {
        edges = new Edge[5000 << 1];
        for (int i = 0; i < edges.length; i++) {
            edges[i] = new Edge();
        }
        head = new int[5000];
        Arrays.fill(head, -1);
        dp = new int[5000];
        cnt = 1;
        ans = 0;
        visited = new boolean[5000];
    }

    private static void dfs(int k, int len) {
        visited[k] = true;
        dp[k] = len;
        for (int i = head[k]; i != -1; i = edges[i].next) {
            int v = edges[i].to;
            if (!visited[v]) {
                dfs(v, len + 1);
            } else {
                ans = Math.max(ans, dp[k] - dp[v] + 1);
            }
        }
    }


    private static void addEdge(int from, int to) {
        edges[cnt] = new Edge(to, head[from]);
        head[from] = cnt++;
    }

    static class Edge {
        int to;
        int next;

        public Edge() {
        }

        public Edge(int to, int next) {
            this.to = to;
            this.next = next;
        }
    }
}