我的第一篇文章

碎碎念

为什么要开始进行记录？maybe是人总有遗忘的时候而数据不会
那么今天的主题就是我于2024.12.11所写的算法题
这将是一个长期更新的频道，将记录我的成长 视我心情而定吧
其实主要是练习markdown语法

题目一 二叉搜索树转双向链表

描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向循环链表。

示例 1：

输入：root = [4,2,5,1,3] 

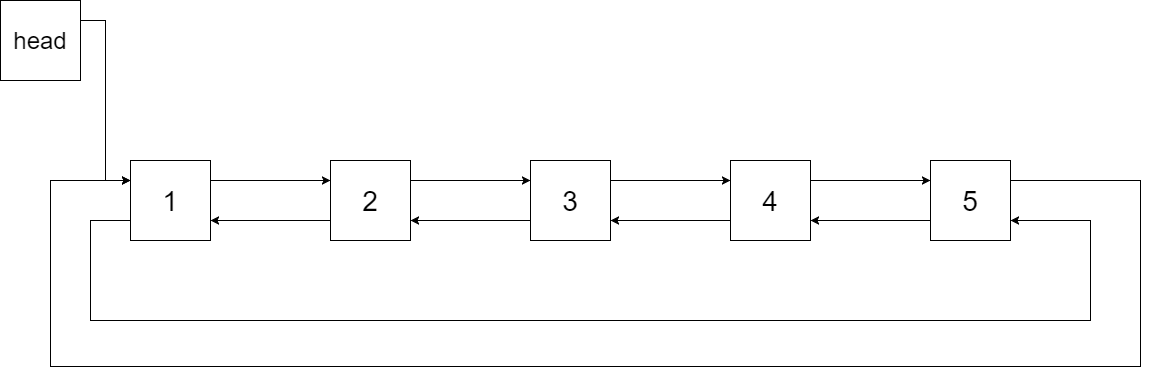
输出：[1,2,3,4,5]

解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系。

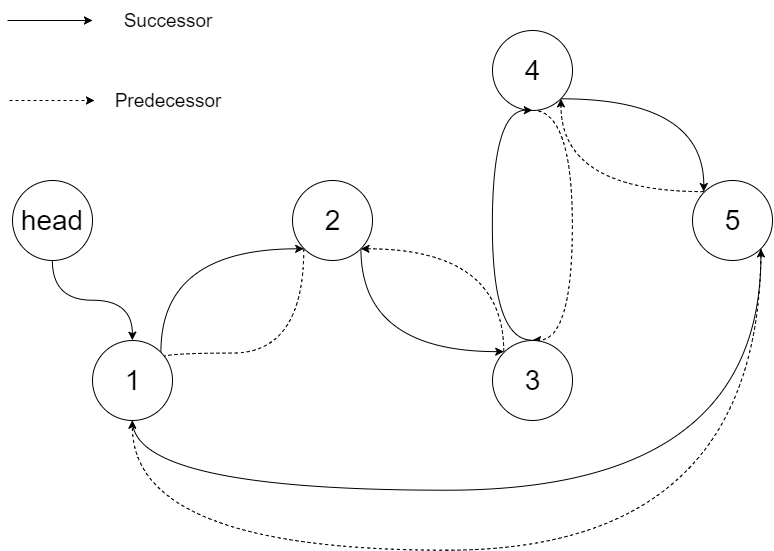
示例 2：

输入：root = [2,1,3]
输出：[1,2,3]

示例 3：

输入：root = []
输出：[]
解释：输入是空树，所以输出也是空链表。

示例 4：

输入：root = [1]
输出：[1]

提示：

• -1000 <= Node.val <= 1000
• Node.left.val < Node.val < Node.right.val
• Node.val 的所有值都是独一无二的
• 0 <= Number of Nodes <= 2000

题目来源 :leetcode 题目难度:中等

题目思路

当看到这题时 想到二叉搜索树右节点大于左节点 即通过中序遍历即可以实现有序
有了大致思路 让我们更加深入的思考一下 究竟应该如何构建这个双向循环链表
我的想法如下

1. 递归左子树：处理左子树的节点并返回到当前节点。

• 前节点的 left 指向中序遍历的前一个节点（即 prev）。
• 如果是第一个访问的节点，则将其作为 头节点。
• 更新 prev 为当前节点。

3. 递归右子树：处理右子树的节点。

递归右子树：处理右子树的节点。

最后将双向链表头尾相连即可
这里题 leetcode 和 牛客 题目大致相同 但是 牛客 是双向链表 而 leetcode 是双向循环链表 即 牛客 不需要连接头尾节点 各位小伙伴做题的时候需注意 我在这里做错了
代码实现如下：

class Solution
{
public:
    // 中序遍历，连接双向链表
    void InOrder(Node *root, Node *&prev, Node *&head)
    {
        if (root == NULL)
            return;
        // 递归左子树
        InOrder(root->left, prev, head);
        // 当前节点处理
        if (prev != NULL)
        {
            prev->right = root; // 上一个节点的右指针指向当前节点
            root->left = prev;  // 当前节点的左指针指向上一个节点
        }
        else
        {
            head = root; // 第一个节点设置为头节点
        }
        prev = root; // 更新前一个节点为当前节点
        // 递归右子树
        InOrder(root->right, prev, head);
    }
    Node *treeToDoublyList(Node *root)
    {
        if (root == NULL)
            return NULL; // 处理空树的情况
        Node *prev = NULL;
        Node *head = NULL;
        // 通过中序遍历将树转换为双向链表
        InOrder(root, prev, head);
        // 由于是双向链表，确保尾节点的右指针指向头节点，头节点的左指针指向尾节点
        if (head != NULL && prev != NULL)
        {
            prev->right = head; // 尾节点指向头节点
            head->left = prev;  // 头节点指向尾节点
        }
        return head; // 返回双向链表的头节点
    }
};

---

题目二 二叉树最近的公共祖先

描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 [2, 105] 内。
• -109 <= Node.val <= 109
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

二叉树最近的公共祖先

当我们看到这题，首先想到进行分类讨论

第一种情况 ：

- 根节点为空
- 根节点 = p
- 根节点 = q

这种情况返回根节点即可

第二种情况 ：p和q在左右两侧 返回根节点即可

第三种情况：p和q在同侧 返回最近的那个被递归找出来的节点即可

代码实现如下：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //如果
        if(root == NULL || root == p || root == q)
            return root;
        TreeNode* left = lowestCommonAncestor(root -> left,p,q);
        TreeNode* right = lowestCommonAncestor(root -> right,p,q);
        if(left && right)
            return root;
        if(left)
            return left;
        return right;
    }
};

算是比较简单的问题，如果还有什么问题可以在评论区给我留言 我看到会及时回复 >ᴗ<✧