java小记-三元运算符、各类运算符优先级、三码、流程控制语句
①三元运算符:
之前
之后:

格式:

计算规则:

范例:
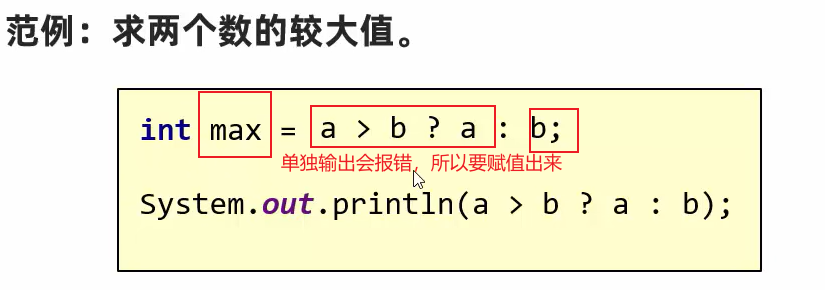
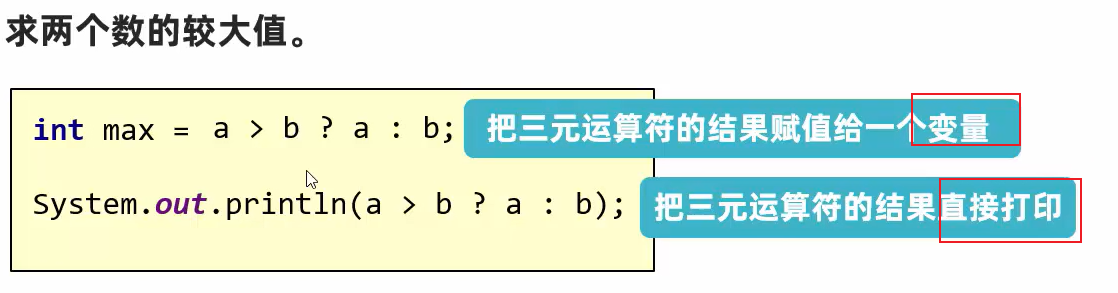
举例:
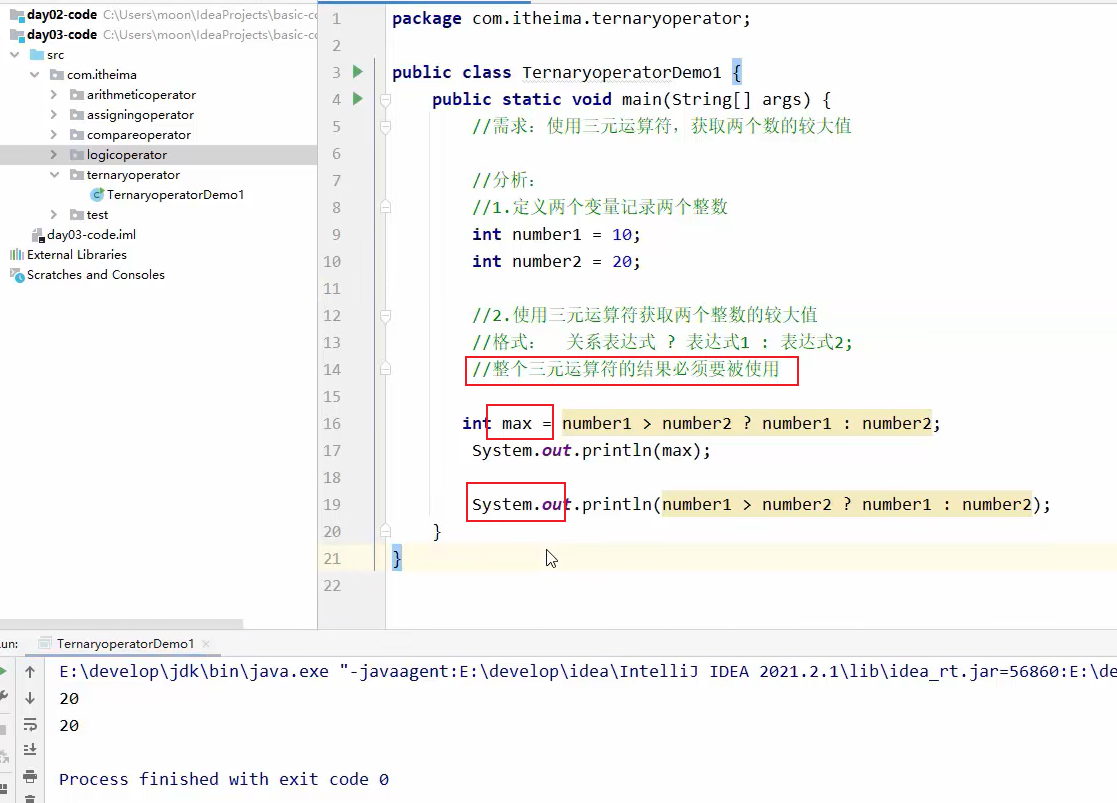
练习1:
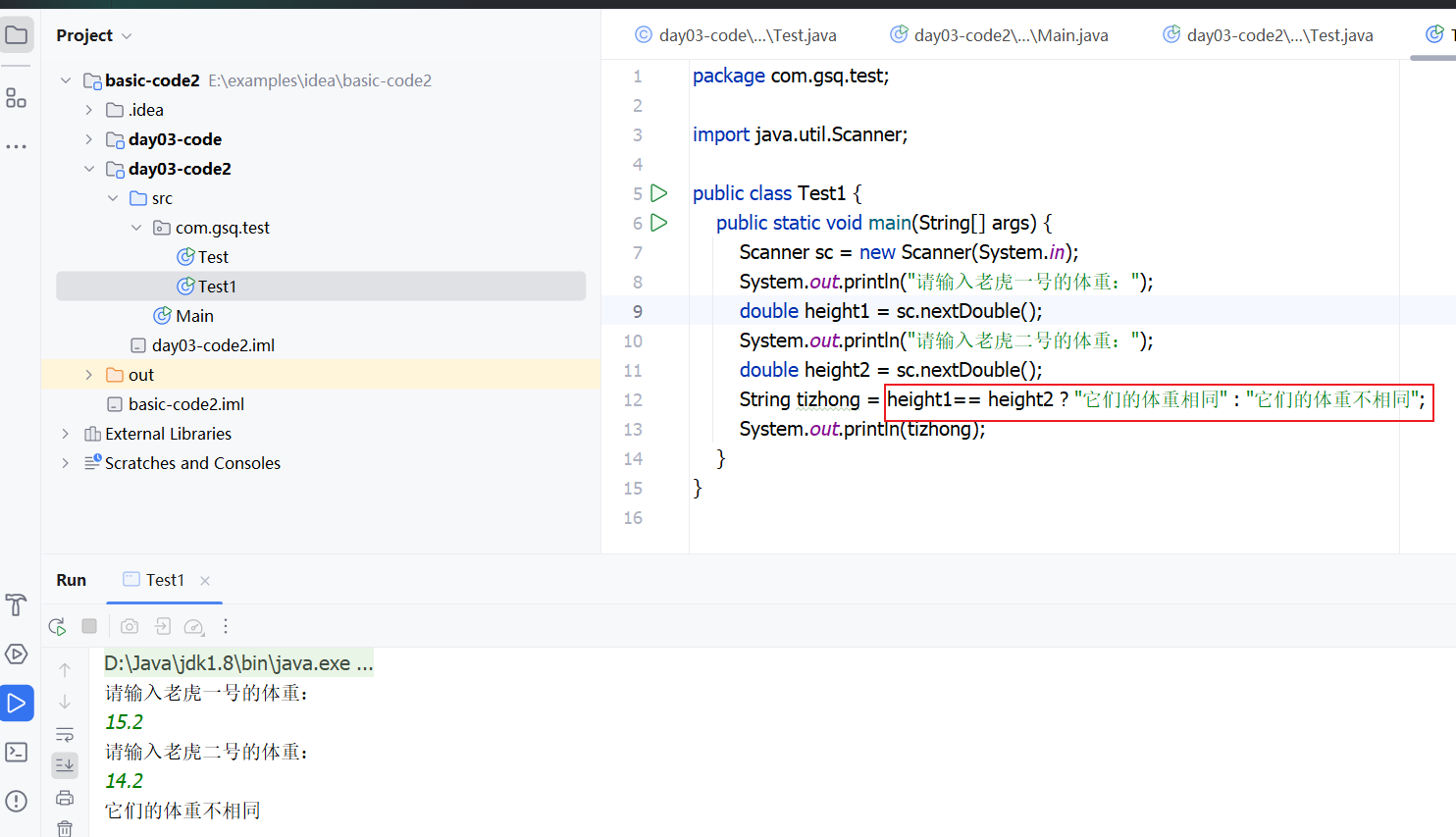
练习二:

我的使用的是三个人输入不同的数据比较大小:(实际上题目已经告知)
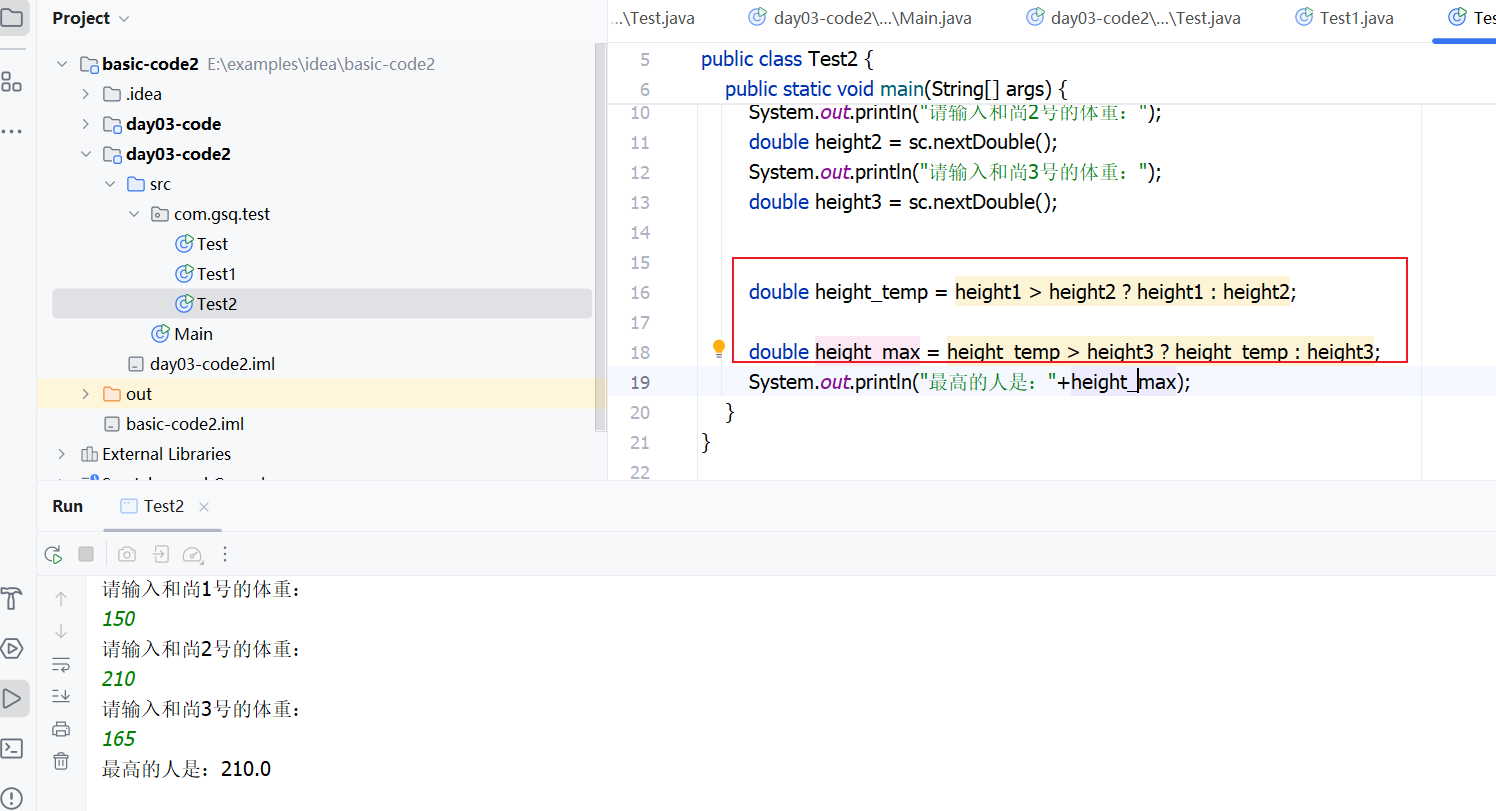
老师的:
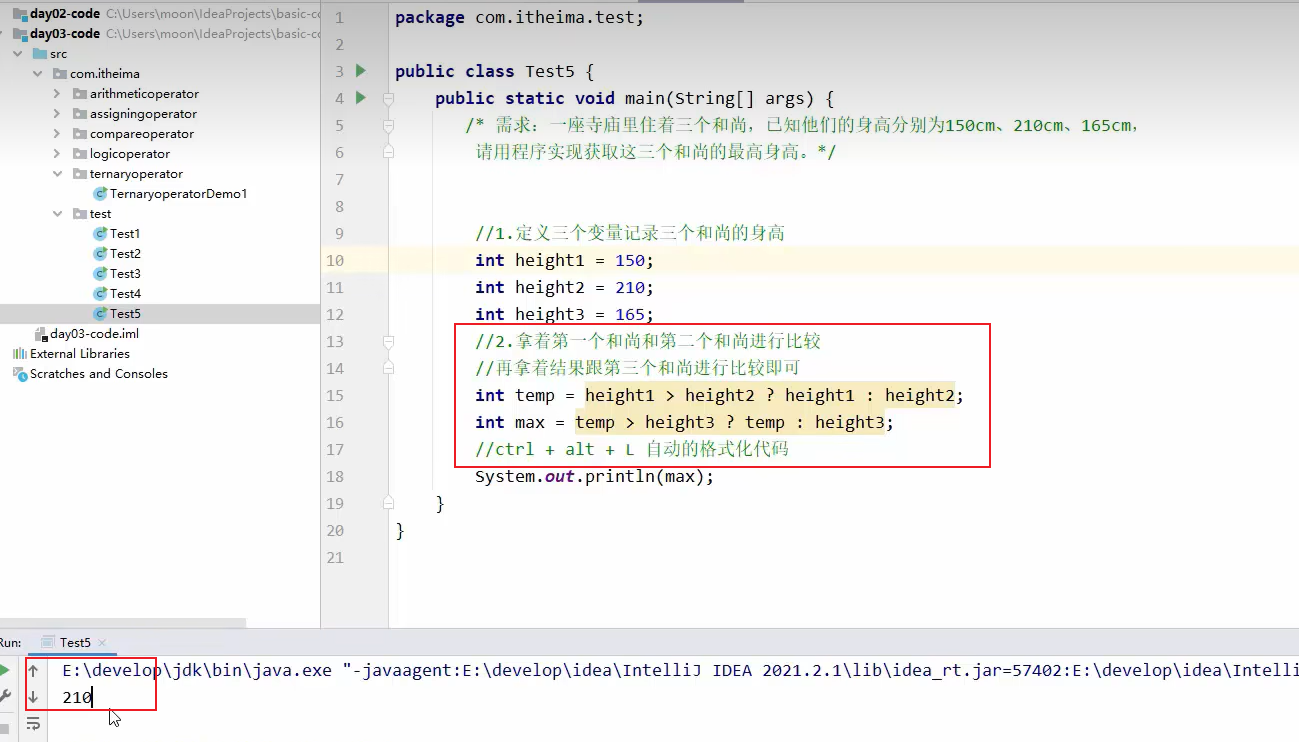
总结一下各类运算符的优先级:
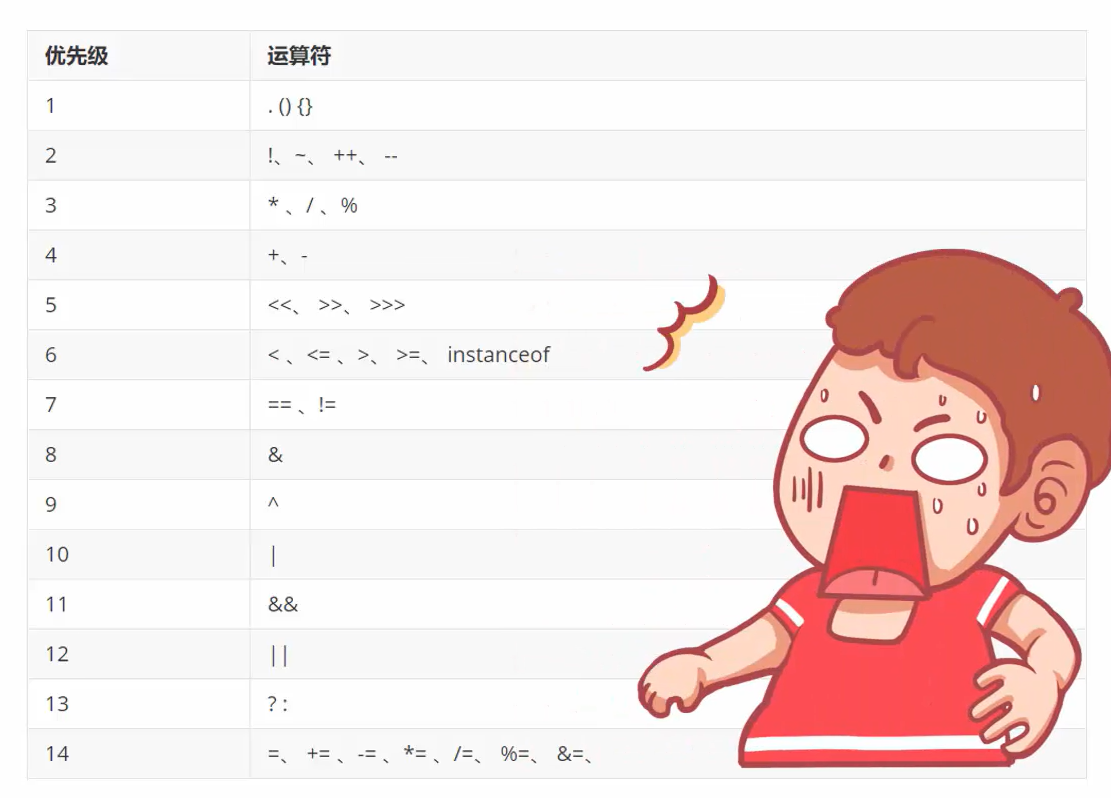
②三种码:(正数一样,负数各不相同)

原码,反码,补码:

各自出现的原因:



字节与比特:

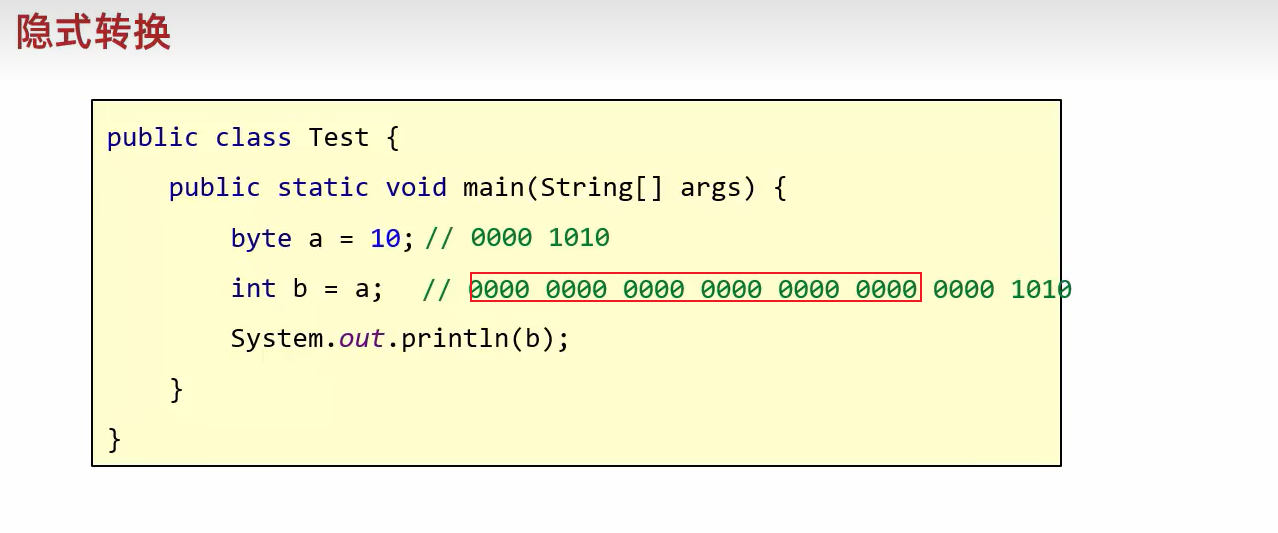
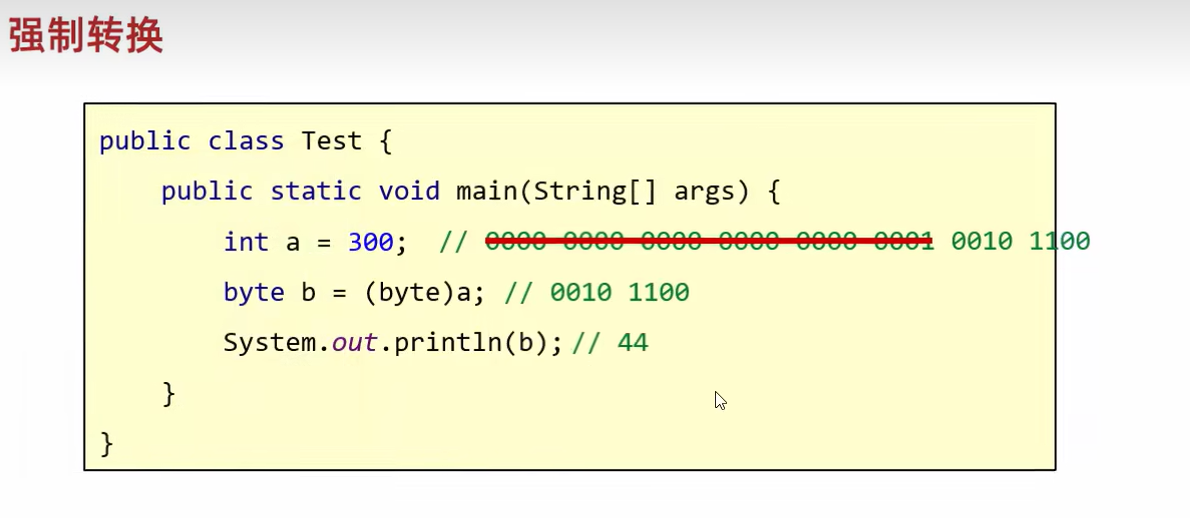
注意负数:
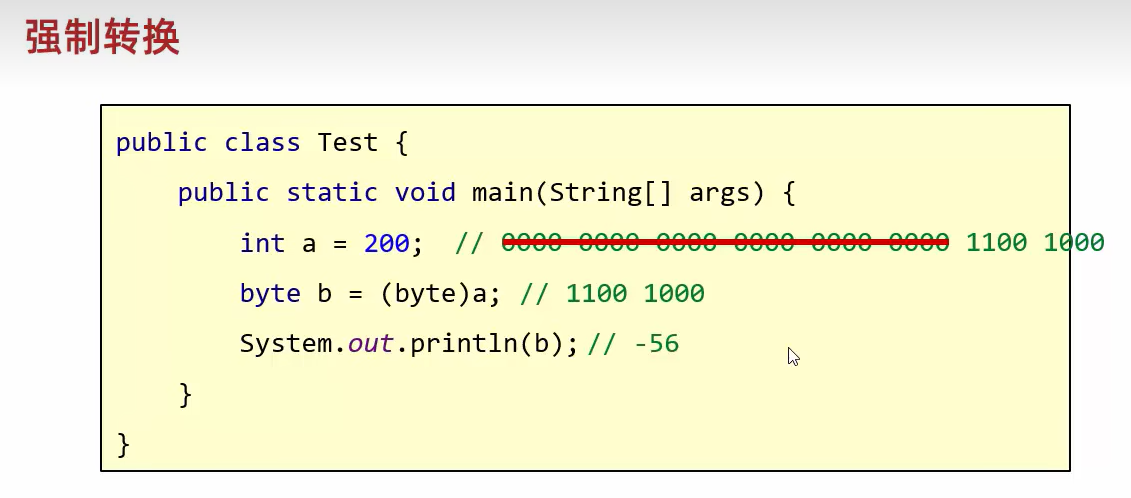
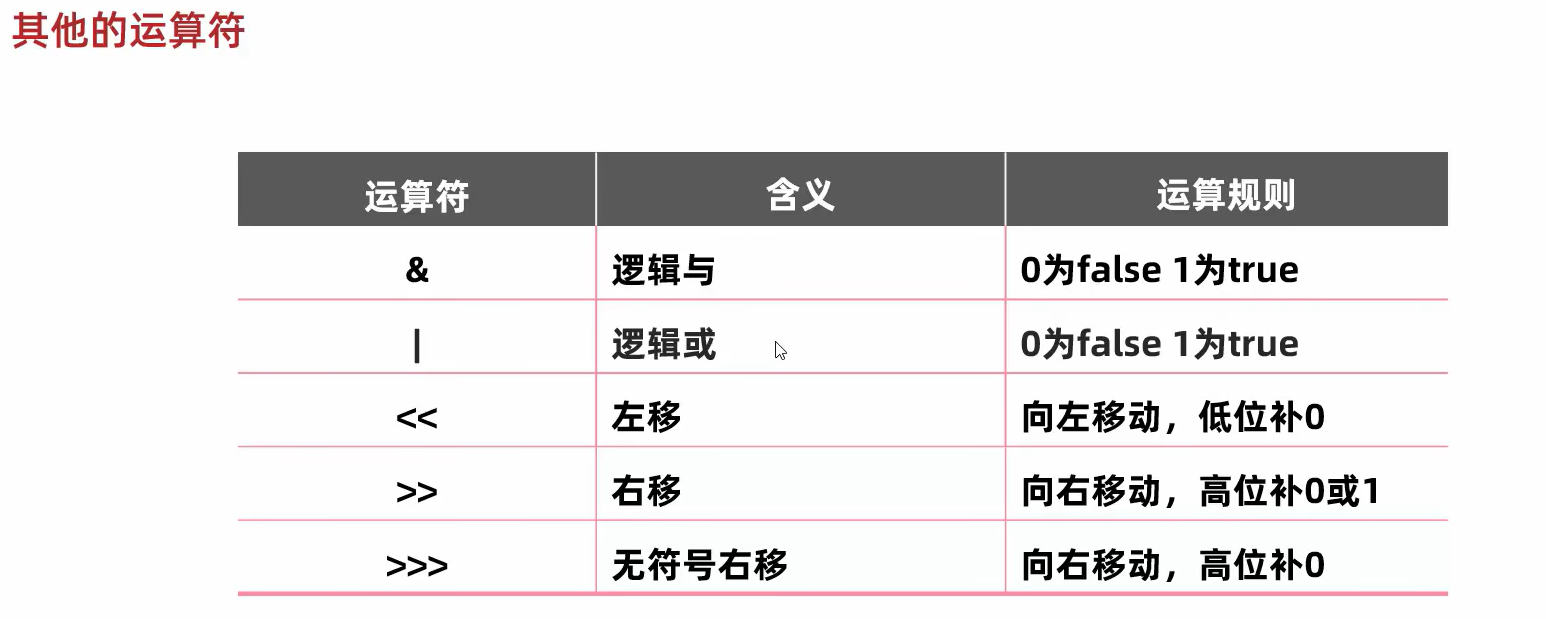
按位与:

按位或:

左移:(乘2)
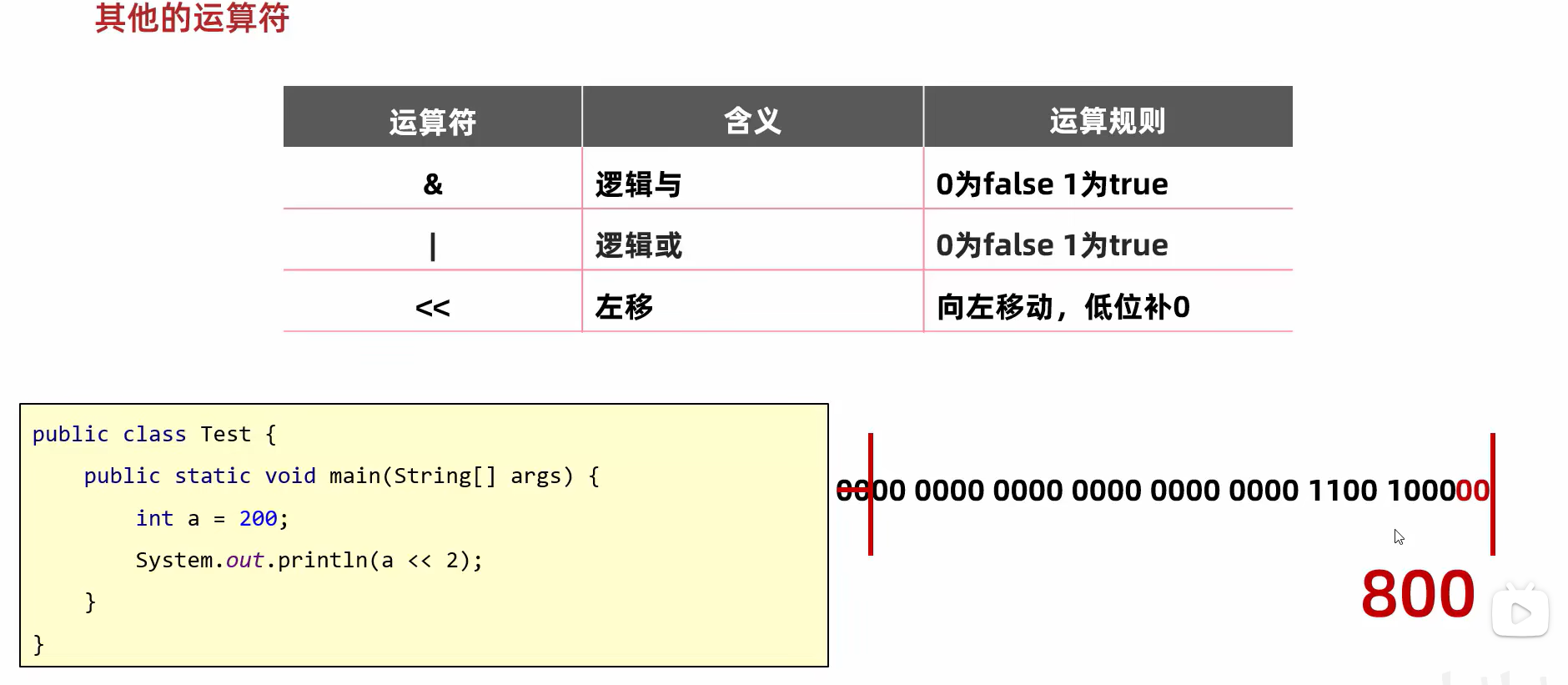
右移:(除2)原码是正补0,是负补1
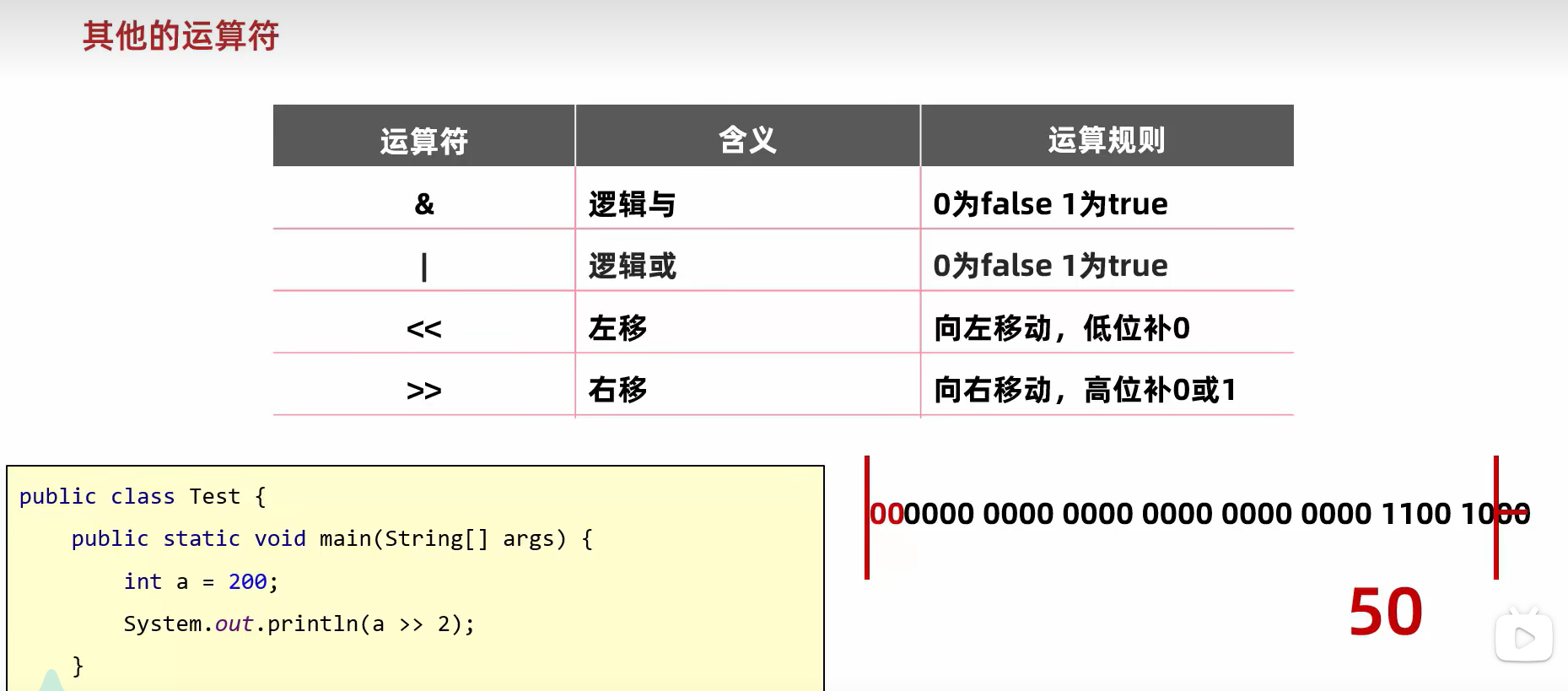

心得:
在计算机内部结构设定了用加法器实现减法,即减去一个数就是加上一个负数。
而这种情况的三种码得到结果各不相同,原码会出现错误结果,反码会导致有时出现0和-0的情况,两个二进制来表示一个数,产生矛盾,
而补码恰恰解决了以上原码和反码的问题,得出正确结果。
补码和时钟的原理类似,还没搞懂(24.6.12后面补起来)。
补充对于补码的自我理解:
举例,比如时钟现在是9点,我让它回到4点,有很多种方法,但一般有两种容易想到的方法:直接回调(减)5个钟,或者顺调(加)7个钟,为什么是7个呢?
这跟时钟的值有关,钟表是12个离散的数,12就是“模”,就比如用一个字节8个比特能表示256个不同状态,就是256个离散的数,256就是模。
回过来,9-5=9+(-5)=4 →-5=(9+7) MOD 12= 16 MOD 12=4,mod是求余,而在模为12时,-5和+7就是“同余”,也能看出规律,-5和+7 取绝对值,为5和7,它们相加的结果刚好等于那个模 12,相当于求一个数5在“模”为12中,它的互补的那个数就是7,+5就是-7,-5就是+7。在计算机中,以无符号8个bit为例,0到255总共256个不同状态,假如现在我要求255-10的结果(结果自然是245嘛),即255+(-10),换算下来就是 255-10=255+246。
这里,-10和+246就是彼此的“互补”的数 → "同余",取绝对值10和246,相加刚好是256,所以+10和-246以及-10和+246这两组就是各自的“同余”。
那么总范围是256个状态时,则255-10 =(255+246)mod 256(它是“模”)= 501 mod 256 = 245(只有256个状态,当加到255时候,就超出范围了,所以又从头开始计数,
比如钟表11点加4点结果是下午三点,原因是11加到12点之后就又从0点(即12点),1点,2点,3点走了,这里跟下午3点是15点的情况无关,15点是24小时制,又要从另一个角度看了。说多了也啰嗦)
说这么多,其实就是补码的作用:
它能通过某种方式,将一个负数转变成一个正数还不会出错的处理,这方便了计算机仅使用加法器就能实现减法的操作,节省了装备减法器的金钱和各种其他资源(话乱理不乱),归根结底就是节约电路成本,以最少的成本实现最大的效益。
③流程控制语句:
顺序结构(默认)从上往下依次执行;
分支结构(if语句和switch语句)
举例:




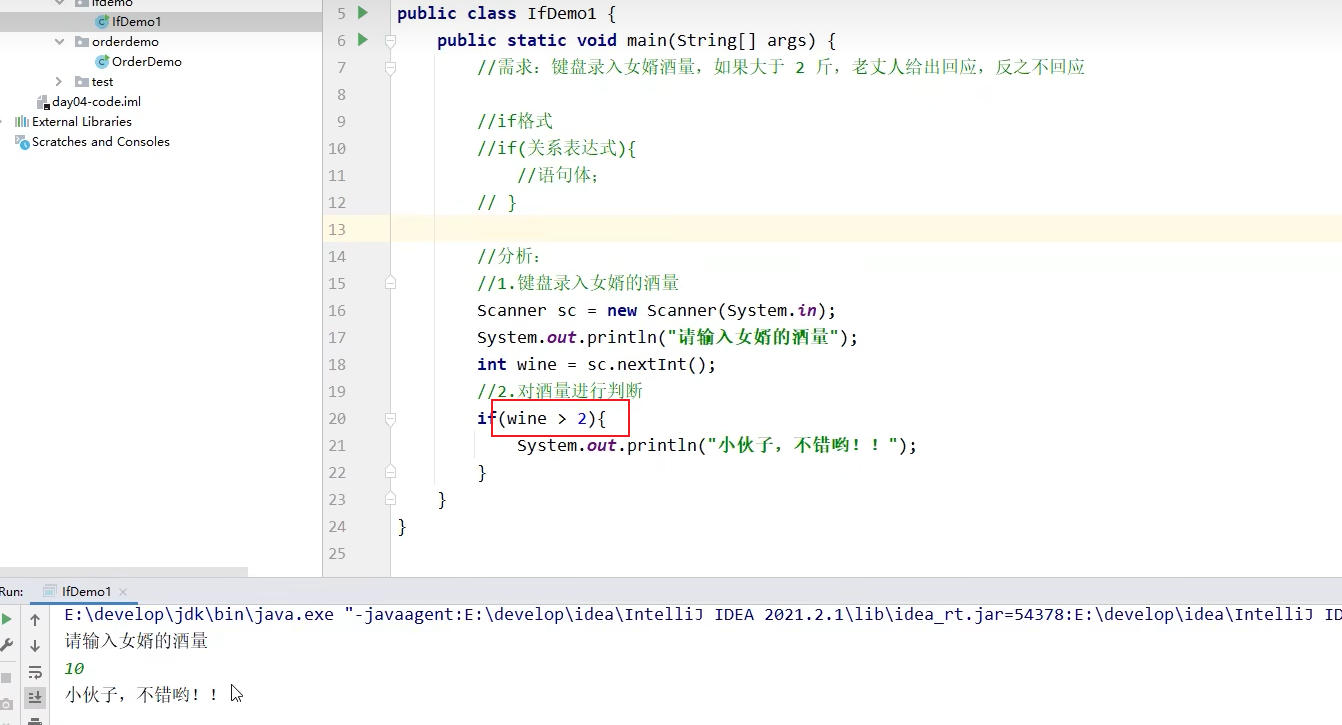

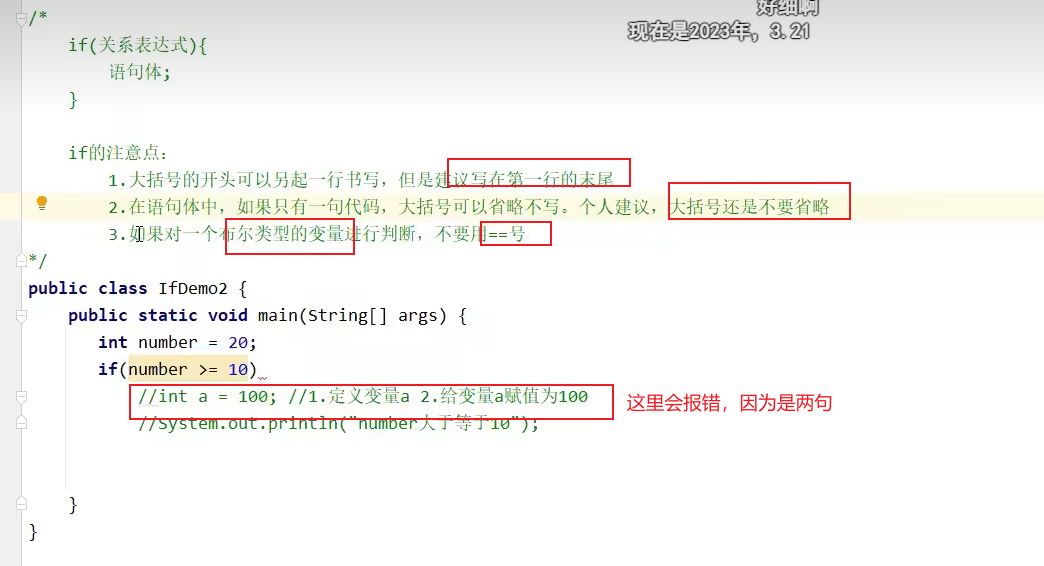
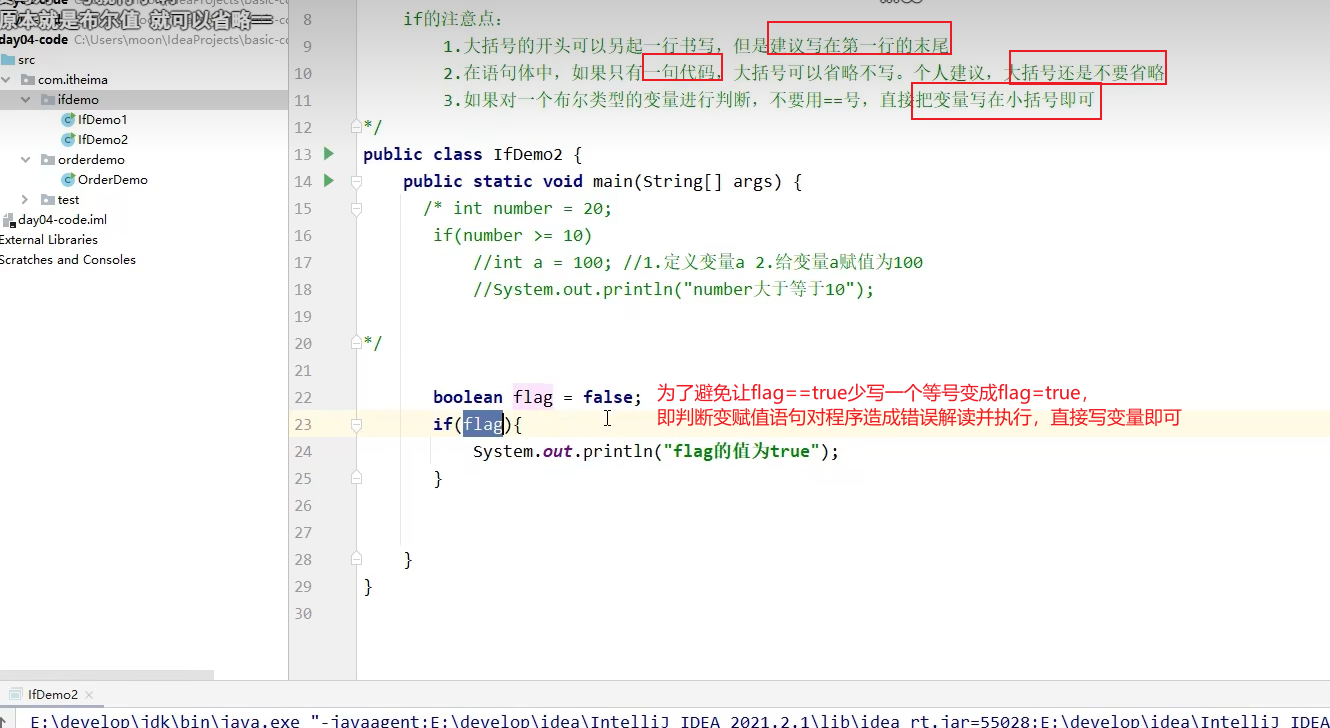
练习:

我也用另一种方式实现:
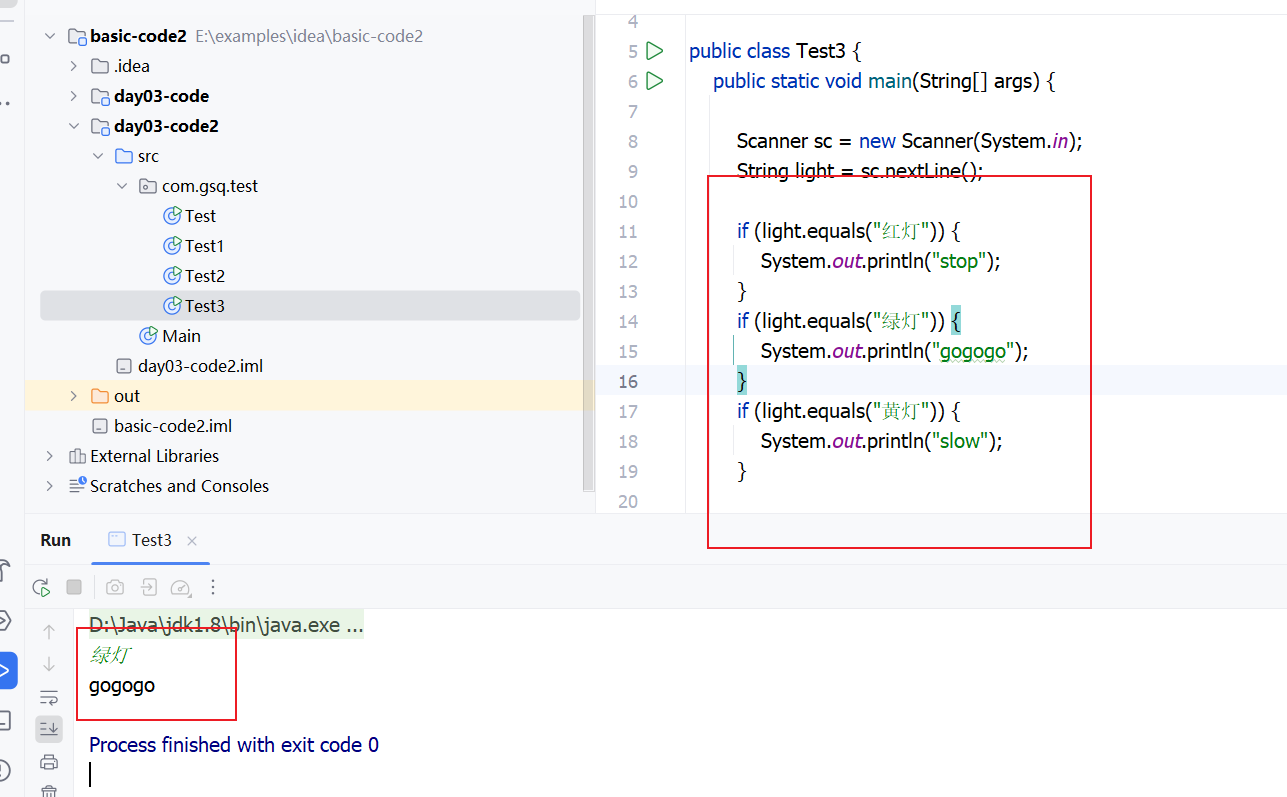


 浙公网安备 33010602011771号
浙公网安备 33010602011771号