机器学习 —— 概率图模型(贝叶斯网络)
概率图模型(PGM)是一种对现实情况进行描述的模型。其核心是条件概率,本质上是利用先验知识,确立一个随机变量之间的关联约束关系,最终达成方便求取条件概率的目的。
1.从现象出发---这个世界都是随机变量
这个世界都是随机变量。
第一,世界是未知的,是有多种可能性的。
第二,世界上一切都是相互联系的。
第三,随机变量是一种映射,把观测到的样本映射成数值的过程叫做随机变量。
上述三条原则给了我们以量化描述世界的手段,我们可以借此把一个抽象的问题变成一个数学问题。并且借助数学手段,发现问题,解决问题。世界上一切都是未知的,都是随机变量。明天会有多少婴儿降生武汉是随机变量,明天出生婴儿的基因也是随机变量,这些孩子智商高低是随机变量,高考分数是随机变量,月薪几何是随机变量。但是这些随机变量之间完全无关么?男孩,智商高,高考低分,月薪高的概率又有多少?显然,随机变量每增多一个,样本空间就会以指数形式爆表上涨。我们要如何快速的计算一组给定随机变量观察值的概率呢?概率图给出了答案。
2.概率图---自带智能的模型
其实在看CRF的时候我就常常在想,基于CRF的词性分割使用了词相邻的信息;基于边缘检测的图像处理使用了像素的相邻信息;相邻信息够么?仅仅考虑相邻像素所带来的信息足够将一个观察(句子或图像)恢复出其本意么?没错,最丰富的关系一定处于相邻信息中,比如图像的边缘对分割的共线绝对不可磨灭,HMM词性分割也效果不错.......但是如果把不相邻的信息引入判断会怎样?在我苦思冥想如何引入不相邻信息的时候Deep Learning 和 CNN凭空出现,不得不承认设计这套东西的人极度聪明,利用下采样建立较远像素的联系,利用卷积将之前产生的效果累加到目前时刻上(卷积的本质是堆砌+变质)。这样就把不相邻的信息给使用上了。但是这样是不是唯一的方法呢?显然不是,还有一种不那么自动,却 not intractable方法,叫做PGM。
还是从快速计算条件概率来谈PGM。首先是representation,概率图的表达是一张。。。图。。。图当然会有节点,会有边。节点则为随机变量(一切都是随机变量),边则为依赖关系(现在只谈有向图)。一张典型的概率图——贝叶斯网络如下所示:

2.1 相关性
对于一副给定的图,每个节点都代表一个随机变量,节点与节点之间通过箭头相连。似乎这在节点与节点之间形成了“流”。那么节点的流之间是否会和随机变量的相关性产生联系?答案是肯定的。考虑几种典型的流:

显然直观的看来,如果x与y直接相连,那么x,y必然是相关的,给出了x的信息则会影响我们对y的判断。当x与y间接相连时,若x,y呈链状关系,那么影响肯定会传递下去,如果x,y不呈链状关系,有共同原因时,则相关;共同发生作用时,则不相关。
这里称 x->W<-y 为 V 结构。
一般情况下,相关性的传递是无法通过V结构的。
但是如果是条件概率的情况下,相关性的传递则表现出完全不同的性质。W 是观测值,如果节点中有随机变量被观测了,那么相关性的连接则会全部取反。也就是说,原本通过W相关的两个变量,在W被观测的情况下,相关性被分离了。也叫做d-separated.记作:d-sepG(X, Y | Z)
上图中,当且仅当,G被观测且没有其他变化的情况下,S会与D相关。
2.2 因式分解
由上述分析可知,当给定某些观测时,原本相关的随机变量可以被分离。
由此我们得出以下定理:

考虑P(D,I,G,L,S)应该怎么计算?如果没有任何先验信息,那么应该是按照条件概率公式:
P(D,I,G,L,S) = P(D)*P(I|D)*P(G|I,D)*P(L|I,D,G)*P(S|D,I,G,L);
上式的最后一项,光是对于P(S|D,I,G,L)就需要考虑DIGL所有的可能,并且每增加一个随机变量,计算的复杂程度就会上升一个档次。使用贝叶斯链式法则,那么上式就可以简化成以下形式:

从概率图的角度上来讲,其表达了在给定父节点的情况下,任意一个节点都是与其非子节点,都是d分离的。
从概率的角度上来讲,任意一个随机变量,在给定父随机变量的情况下,和其非子随机变量,都是d分离的。
或者再通俗一点,一个聪明人,在一场很难的考试里拿了高分,却得到了一封很烂的推荐信,同时他SAT考试却是高分的概率是多少?
我们再隐藏一些细节,一个人推荐信很烂,他SAT高分的概率是多少?或者,一个人SAT低分,却手握牛推的概率是多少?
如果不考虑随机变量之间的依赖关系,上述内容是很难计算的。但是如果有一个构建好的概率图,上面的问题则可以转化为条件概率问题。
通过观察实验,我们可以得到一系列的条件概率,通过此条件概率,以及贝叶斯条件概率链式法则,则可求的我们想要的那一组随机变量的概率。


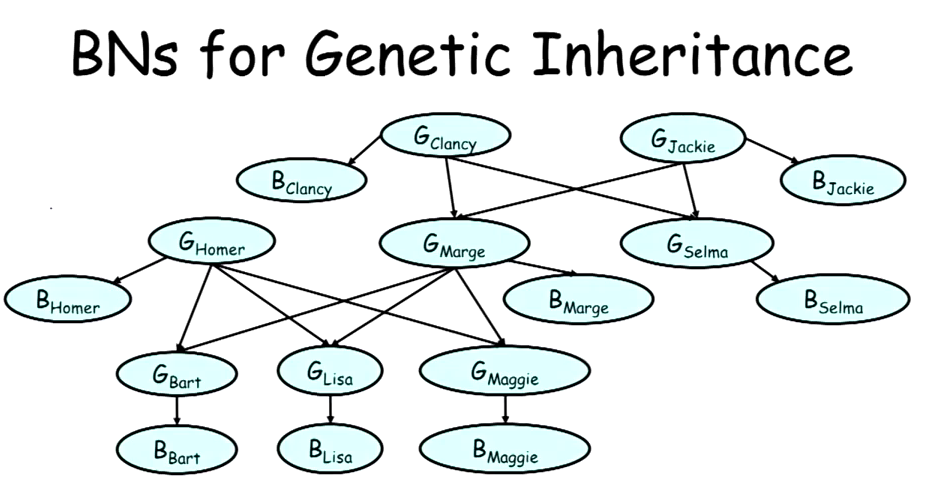
OK,玩具例子结束了,接下来我们来一点真的。如何通过某人血型(A B AB O)及其父母血型推测其基因型(AAAO AB BB BO ....),首先,我们可以建立一张概率图,所有的血型B,基因型G,都是随机变量(节点)。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号