Activation function

一、Activation function

1. Sigmod
   \[g(z) = \frac{1}{1 + e^{-z}} \]

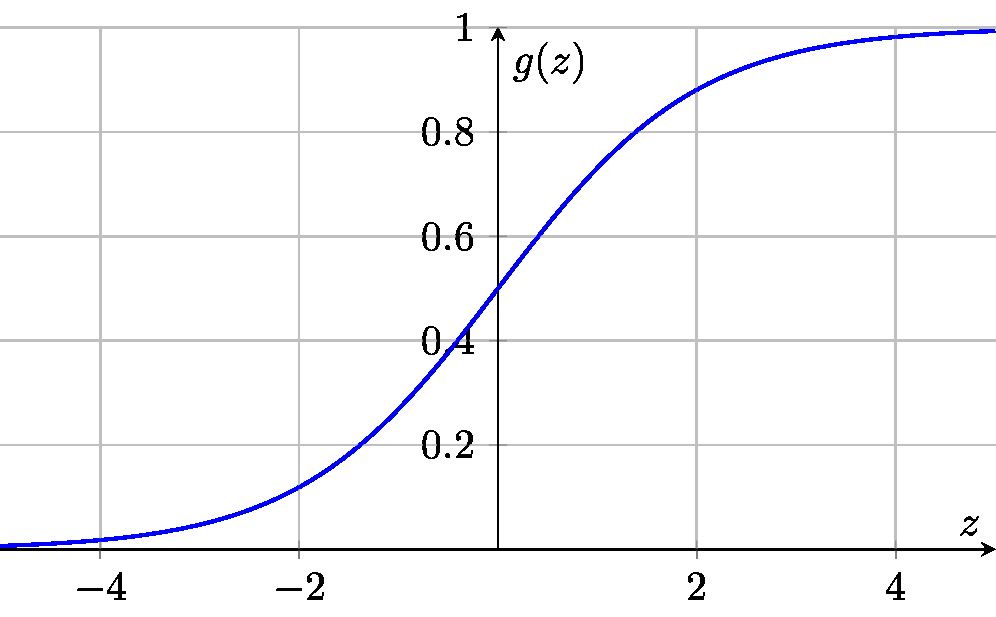
For Binary Classification(Logistic regression)/Output layer is binary.

---

2. ReLU——most common choice(faster)
   \[g(z) = \max(0,z) \]

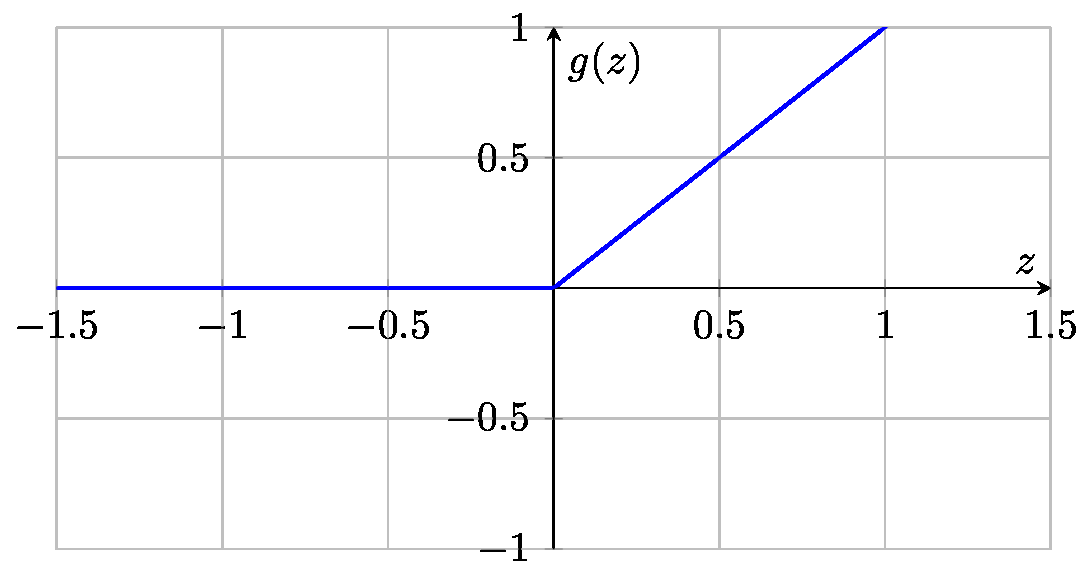
For Regression，y≥0

# hidden layers are recommended to use ReLU
    from tf.keras.layers import Dense
    model = Sequential([
      Dense(units=25, activation='relu'),
      Dense(units=15, activation='relu'),
      Dense(units=1, activation='sigmoid') # or 'linear'/'relu'
    ])

---

3. Linear activation function

\[g(z) = z \]

there is no g!
For Regression，y=+/-

---

4. Softmax由于浮点数计算会有误差，存在改进

\[z_j = \vec{w}_j \cdot \vec{x} + b_j \]

\[a_j = \frac{e^{z_i}}{e^{z_1}+e^{z_2} +...+ e^{z_j}+...+e^{z_n}}=\frac{e^{z_j}}{\sum_{k=1}^{N} e^{z_k}}=P(y=j| \vec{x}) \]

\[a_1 + a_2 + \ldots + a_N = 1 \]

For Multiclass（used in output layer）

---

5. Tahn

---

6. Leaky ReLU

---

7. Swish

---

二、How to choose activation functions

1. Dont use linear activations in hidden layers, cause that equals one linear function, instead gengerate more new and complex features.

2. Multiclass：

---

三、Example———Multiclass Classification

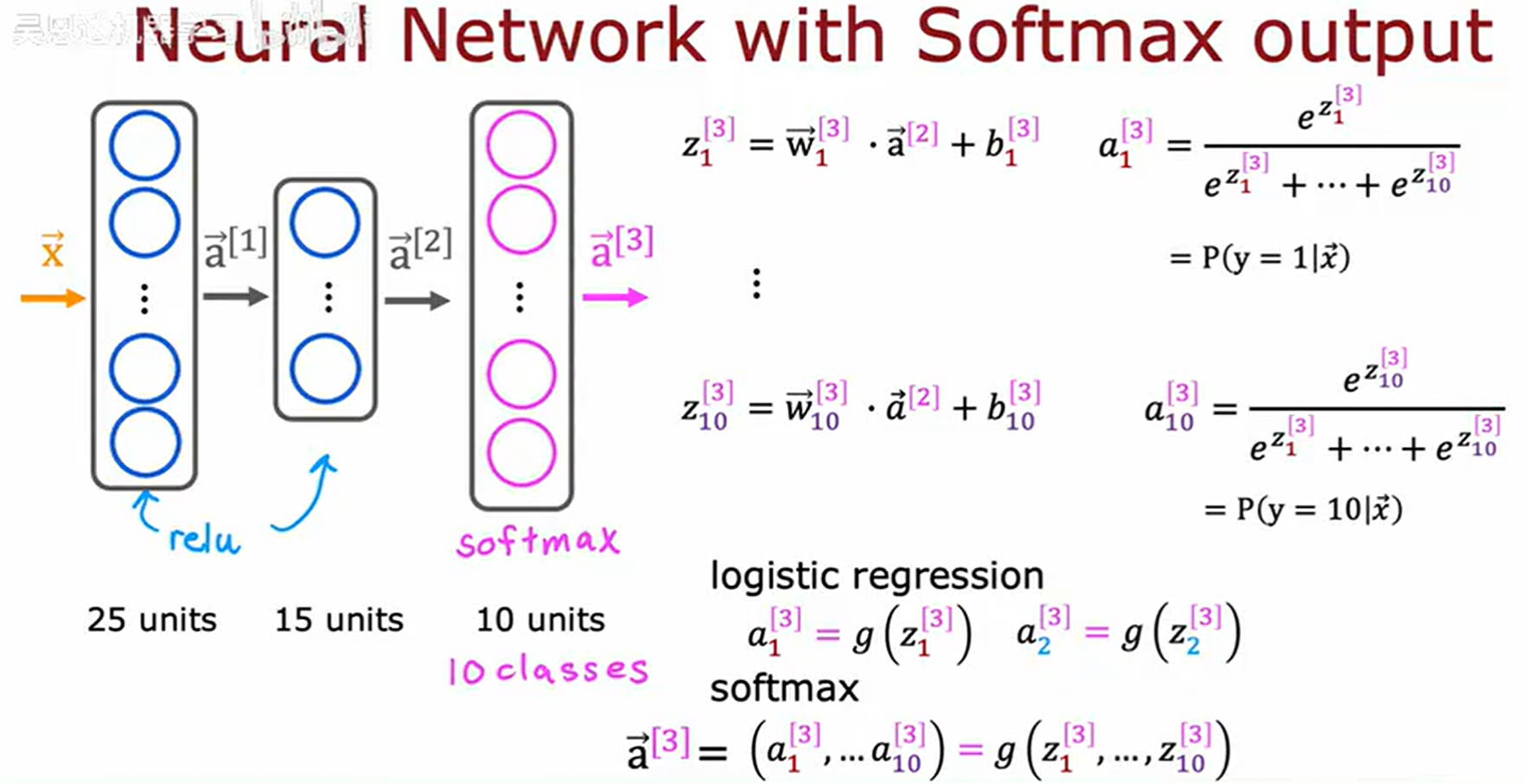
# step1——specify the model
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
model = Sequential([
  Dense(units=25, activation='relu')
  Dense(units=15, activation='relu')
  Dense(units=10, activation='softmax')# 识别数字1-10，output layer有10个神经元
                  ])#如果输出层函数改为'linear',则输出z1..z10而不是a1..a10
#step2—specify loss and cost
from tensorflow.keras.losses import SparseCategoricalCrossentropy
model.compile(loss=SparseCategoricalCrossentropy(from_logits=True))  
#step3——train the model
model.fit(X,Y,epochs=100)
#step4——predict
logit = model(X)
f_x = tf.nn.softmax(logits)
# DONT USE THIS VERSION SHOWN HERE!

改进

\[\text{loss} = -y \log \left( \frac{1}{1 + e^{-z}} \right) - (1 - y) \log \left( 1 - \frac{1}{1 + e^{-z}} \right) \]

另一个例子

multi-class classification and multi-label classification

---

SparseCategoricalCrossentropy 稀疏类别交叉熵函数

1.基本概念

SparseCategoricalCrossentropy 是一种用于多分类问题（multi-class classification）的损失函数，适用于整数标签（integer labels）的情况。

2.适用场景

当分类任务的标签是整数形式（如 0, 1, 2, ...），而不是 one-hot 编码形式（如 [1, 0, 0], [0, 1, 0]）时，使用这个损失函数。

3.计算原理

该损失函数计算真实标签（ground truth）和模型预测的概率分布之间的交叉熵（cross-entropy），用于衡量预测的误差。

与 CategoricalCrossentropy 的区别

损失函数	适用标签类型	示例
SparseCategoricalCrossentropy	整数标签	y = [0, 1, 2]
CategoricalCrossentropy	one-hot 编码标签	y = [[1,0,0], [0,1,0]]

使用方法

from tensorflow.keras.losses import SparseCategoricalCrossentropy

# 基础用法
model.compile(
    optimizer='adam',
    loss=SparseCategoricalCrossentropy(),
    metrics=['accuracy']
)

# 高级配置（当模型输出未经过 softmax 时）
loss_fn = SparseCategoricalCrossentropy(from_logits=True)
model.compile(optimizer='adam', loss=loss_fn)