Java 中 double 的精度问题，以及为什么 BigDecimal 没有这个问题

Java 中 double 的精度问题，以及为什么 BigDecimal 没有这个问题

当你在 Java 中写出：

System.out.println(0.1 + 0.2); // 0.30000000000000004

是不是很诧异？这不是 Java 的“bug”，而是计算机数值表示方式导致的。本文系统解释 为什么 double（IEEE 754 二进制浮点）会出现精度问题，以及 BigDecimal 为什么能精确表示十进制小数。

---

一、问题概览：现象与根源

现象：

• 使用 double 进行十进制计算时，常会看到奇怪的结果：

  System.out.println(0.1 + 0.2); // 0.30000000000000004
  

原因：

• double 使用 IEEE 754 二进制浮点标准（基数 2）。

• 很多十进制有限小数（如 0.1）在二进制下是无限循环小数，计算机只能存有限位数 → 截断 → 误差。

后果：

• 在金融、计费、利率、货币运算等场景中，这种微小误差可能引起严重问题。

• 因此此类场景应使用 BigDecimal（十进制精确数）来代替 double。

---

二、二进制与十进制表示小数的区别

任意进制的小数都可以写作：
[
0.d_1d_2d_3..._b = d_1·b^{-1} + d_2·b^{-2} + d_3·b^{-3} + ...
]

例如：

• 十进制：0.1 = 1×10⁻¹

• 二进制：0.1₂ = 1×2⁻¹ = 0.5₁₀

只有分母是底数的幂时，小数才能有限表示：

例子	分母	十进制能否有限	二进制能否有限
1/2	2	✅	✅
1/5	5	✅	❌
1/10 (=0.1)	2×5	✅	❌
1/8 (=0.125)	8	✅	✅

也就是说：

十进制能精确表示分母含 2、5 的分数；
二进制只能精确表示分母是 2ⁿ 的分数。

因此，0.1（=1/10）在二进制中是无限循环小数。

---

三、0.1 的二进制展开（为什么无限循环）

转换规则：
每次“乘以 2，取整数部分作为当前二进制位，小数部分继续乘 2”。

以 0.1 为例：

0.1 × 2 = 0.2 → 0
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1 (余 0.6)
0.6 × 2 = 1.2 → 1 (余 0.2)

余数又回到 0.2 → 循环出现！

因此：

0.1₁₀ = 0.0001100110011...₂

即 0.(0011)₂ 无限循环。计算机只能存有限位（double 仅 53 位有效位），因此必须截断或舍入。

---

四、IEEE 754 double 的结构与近似误差

double 占 64 位：

部分	位数	说明
符号位	1	表示正/负
指数	11	偏移量 1023
尾数（mantissa）	52	实际有效精度约 15~17 位十进制数

double 在存储 0.1 时，会存成一个最接近 0.1 的二进制浮点数：

0.1000000000000000055511151231257827021181583404541015625

当你做 0.1 + 0.2 时，其实是两个近似数相加，误差传播后就看到：

0.30000000000000004

---

五、BigDecimal：为什么它不会有这个问题

BigDecimal 是十进制数的精确实现。
它不是浮点数，而是：

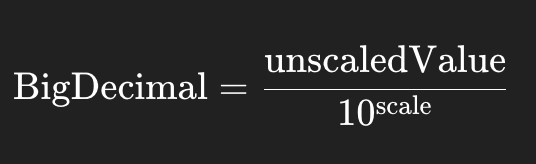
即：

• unscaledValue：一个整数（BigInteger）

• scale：小数位数（十进制）

例如：

BigDecimal x = new BigDecimal("0.003");
System.out.println(x.unscaledValue()); // 3
System.out.println(x.scale());         // 3
// 表示 3 ÷ 10³ = 0.003

再如：

BigDecimal y = new BigDecimal("0.234");
System.out.println(y.unscaledValue()); // 234
System.out.println(y.scale());         // 3
// 表示 234 ÷ 10³ = 0.234

这意味着 BigDecimal 直接存储十进制结构，没有任何二进制浮点参与，因此不会出现“无限循环导致误差”。

---

六、构造 BigDecimal 的正确方式

✅ 推荐写法：

BigDecimal bd1 = new BigDecimal("0.1");       // 字符串精确
BigDecimal bd2 = BigDecimal.valueOf(0.1);     // 内部等价于 new BigDecimal("0.1")

❌ 错误写法：

BigDecimal bd3 = new BigDecimal(0.1); // 把 double 的误差一并带入
System.out.println(bd3);
// 0.1000000000000000055511151231257827021181583404541015625

---

七、两者比较的本质区别

特性	double	BigDecimal
基数	2（二进制）	10（十进制）
能精确表示的数	n/2ⁿ	n/10ⁿ
存储结构	符号 + 指数 + 尾数	BigInteger + scale
精度	固定（约15位十进制）	任意（受内存限制）
性能	快（硬件支持）	慢（软件实现）
误差来源	二进制无法精确表示十进制	无（除非除法需舍入）

---

八、实践建议

• 使用 double 的场景：

  • 科学计算、统计分析、图形渲染等对微小误差不敏感、追求性能的场景。

• 使用 BigDecimal 的场景：

  • 金融、税务、计费等对精度要求极高的场景。

  • 需要精确比较或精确小数运算时。

建议：

• 使用 new BigDecimal(String) 或 BigDecimal.valueOf(double)

• 明确指定 RoundingMode（舍入方式）和 scale（小数位数）

---

九、示例代码（对比）

public class PrecisionDemo {
    public static void main(String[] args) {
        double a = 0.1;
        double b = 0.2;
        System.out.println("double 0.1 + 0.2 = " + (a + b));
        // 0.30000000000000004

        BigDecimal bd1 = new BigDecimal("0.1");
        BigDecimal bd2 = new BigDecimal("0.2");
        System.out.println("BigDecimal(\"0.1\") + BigDecimal(\"0.2\") = " + bd1.add(bd2));
        // 0.3

        BigDecimal fromDouble = new BigDecimal(0.1);
        System.out.println("new BigDecimal(0.1) = " + fromDouble);
        // 0.1000000000000000055511151231257827021181583404541015625
    }
}

---

十、小结（重点回顾）

1. double 是 二进制浮点数，只能精确表示分母为 2ⁿ 的分数。

2. 十进制小数（如 0.1）在二进制中变成 无限循环，只能近似。

3. BigDecimal 用十进制结构（unscaledValue / 10^scale）存数，能精确表示所有十进制有限小数。

4. 构造时应使用 字符串或 valueOf，不要直接传入 double。

5. 十进制并不是万能精确——像 1/3 在十进制中也会无限循环，但 BigDecimal 可以用设定精度来控制结果。

---

🔍 一句话总结：
二进制浮点数 double 对十进制小数“天生不友好”；
而 BigDecimal 以十进制整数 + 小数位数的方式存储，天生适合精确的十进制运算。