日日算法:Dijkstra算法
介绍
Dijistra算法作为一种最短路径算法,可以用来计算一个节点到图上其他节点的最短距离。
主要是通过启发式的思想,由中心节点层层向外拓展,直到找到中点。
适用于无向图和有向图。
算法思想
- 假设我们要计算节点
A到其它节点的最短距离 - 引入两个集合(
S,U),其中集合S表示已经求出最短路径的点(以及最短距离),集合U表示还未求出最短路径的点。集合中的元素用类似A(0)形式表示,其中A目标点为A,(0)表示目前已知最短路径为0(未直接连通的距离用∞表示)。 - 初始时,
S集合中只有起始点,距离为0,U集合中除了直接与A点连通的点外,距离都为∞。 - 第一次向外拓展,找出
U集合中距离最短的点(假设为B)加入集合S。并以B点向外拓展,更新U集合中的距离值。更新规则为,如果经过B到某点的距离小于U集合中记录的结果,那么则更新中集合U中该点的距离值。 - 每执行一次步骤四,我们可以得出
A点距某个点的最短距离。 - 重复步骤四,直到
U的集合为空或是目标点不在U集合中,也就计算出了需要的最短距离。
用图表示解题过程:
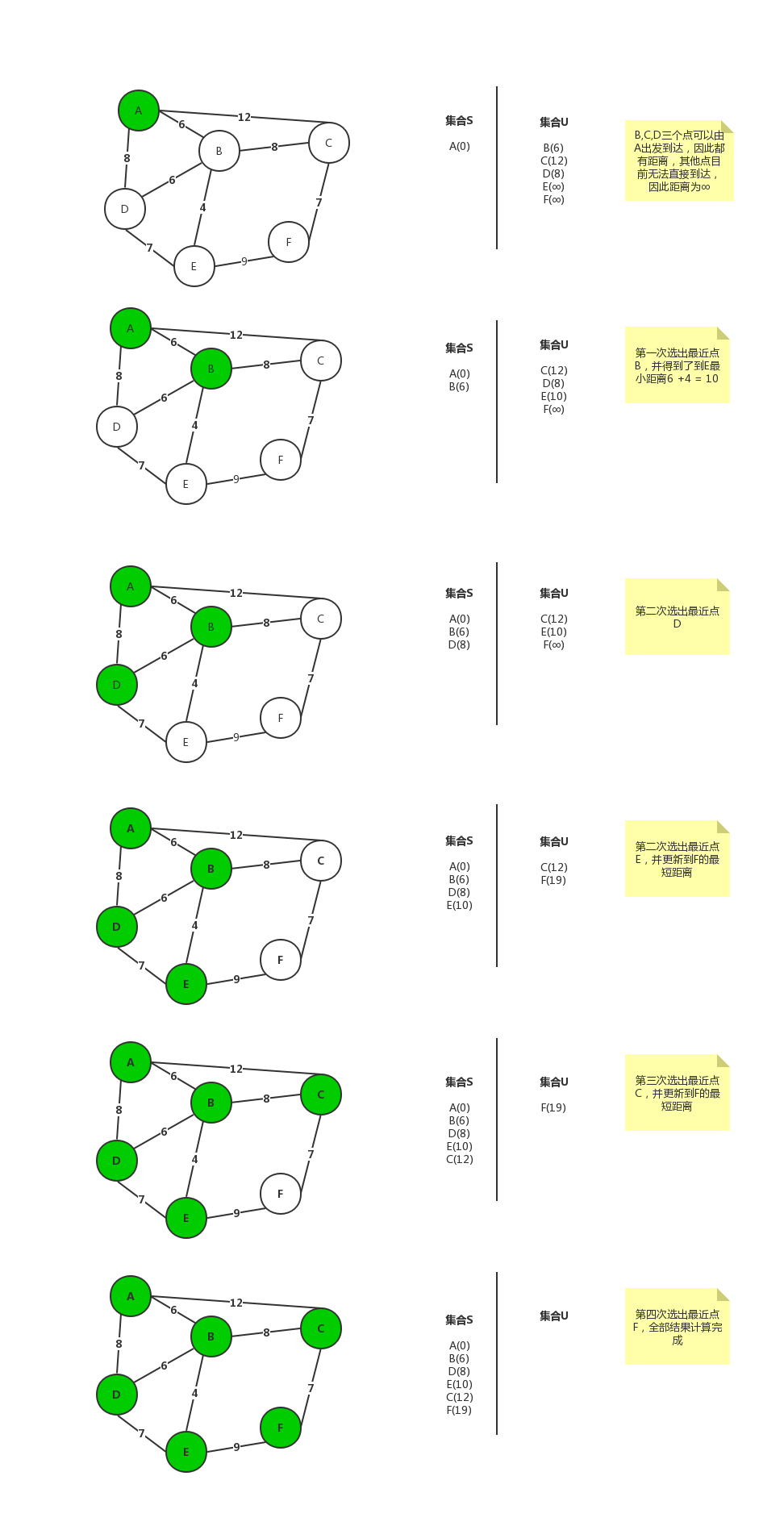
证明
同样以上图为例,我们如何保证第一次选择得到结果A-> B (6)是正确的最优解。
证明:
- 上述图为无向图,且不存在负权边。
- 由A出发去其他点,穷举第一条边所有选择,只能为
A -> B(6),A -> C(12)和A -> D(8)三种。一旦第一条边选择了后两种情况,经过C或是D点再绕回B,由于不存在负权边,那么经过C的路线一定大于A->C(12),经过D的路线A->D(8),因此都会大于A ->B(6)。 - 那么为什么第二次选择只能确定
D而非刚更新了最小值的E点。首先基于上一步我们确定了由A出发去D点最短路径第一条边只可能是A->B和A->D两种情况,而经过B点再选择第二条边也在上轮计算过了,其与第一条边之和均大于A->D(8),所以能够确定到D的最短路径。而由于D->E的最短路径在第二轮尚不知道,因此无法确定到E的最短路径。 - 同理,可以确定每一轮的解都是最短路径。
算法实现
public class Dijkstra {
public static int[] getShortestPath(int[][] graph, int source){
if(graph == null || graph.length <= source)
throw new IllegalArgumentException();
if(graph.length != graph[0].length)
throw new IllegalArgumentException();
int n = graph[source].length;
// String[] route = new String[n];
//保存结果集
int[] ret = new int[graph[source].length];
//保存已确定最短路径的点
int[] visited = new int[graph[source].length];
//初始化数据
Arrays.fill(visited, 0);
Arrays.fill(ret, Integer.MAX_VALUE);
ret[source] = 0;
//进行n次筛选
for(int i=0; i<n; i++){
//找出结果集中未visited结果中数据最小的点,为该轮确定的最短路径
int minValueIndex = findMinValue(ret, visited);
visited[minValueIndex] = 1;
//更新通过该点是否有新的最短路径生成
int[] line = graph[minValueIndex];
for(int j=0; j<line.length; j++){
if(visited[j] == 0 &&
line[j] != Integer.MAX_VALUE &&
line[j] + ret[minValueIndex] <= ret[j]){
ret[j] = line[j] + ret[minValueIndex];
}
}
}
return ret;
}
private static int findMinValue(int[] source, int[] visited){
int ret = 0;
int minVal = Integer.MAX_VALUE;
for(int i=0; i<source.length; i++){
if(visited[i] == 0 && source[i] < minVal){
ret = i;
minVal = source[i];
}
}
return ret;
}
}
上述代码见Github。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号