HDU 4237 The Rascal Triangle
The Rascal Triangle
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 243 Accepted Submission(s): 192
Problem Description
The
Rascal Triangle definition is similar to that of the Pascal Triangle.
The rows are numbered from the top starting with 0. Each row n contains
n+1 numbers indexed from 0 to n. Using R(n,m) to indicte the index m
item in the index n row:
R(n,m) = 0 for n < 0 OR m < 0 OR m > n
The first and last numbers in each row(which are the same in the top row) are 1:
R(n,0) = R(n,n) = 1
The interior values are determined by (UpLeftEntry*UpRightEntry+1)/UpEntry(see the parallelogram in the array below):
R(n+1, m+1) = (R(n,m) * R(n,m+1) + 1)/R(n-1,m)

Write a program which computes R(n,m) the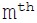 element of the
element of the row of the Rascal Triangle.
row of the Rascal Triangle.
The first and last numbers in each row(which are the same in the top row) are 1:
The interior values are determined by (UpLeftEntry*UpRightEntry+1)/UpEntry(see the parallelogram in the array below):

Write a program which computes R(n,m) the
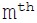 element of the
element of the row of the Rascal Triangle.
row of the Rascal Triangle.
Input
The
first line of input contains a single integer P, (1 <= P <=
1000), which is the number of data sets that follow. Each data set is a
single line of input consisting of 3 space separated decimal integers.
The first integer is data set number, N. The second integer is row
number n, and the third integer is the index m within the row of the
entry for which you are to find R(n,m) the Rascal Triangle entry (0
<= m <= n <= 50,000).
Output
For
each data set there is onr line of output. It contains the data set
number, N, followed by a single space which is then followed by thr
Rascal Triangle entry R(n,m) accurate to the integer value.
Sample Input
5
1 4 0
2 4 2
3 45678 12345
4 12345 9876
5 34567 11398
Sample Output
1 1
2 5
3 411495886
4 24383845
5 264080263
Source
解析:利用题中所给递推公式,将数据存放到数组中有时候是个不错的选择。但本题这样做很可能会MLE,所以应该考虑找出通项公式。可以先写个小程序输出The Rascal Triangle的前几行,观察找规律。
很容易发现通项公式为1+(n-m)*m。
1 #include <cstdio> 2 3 int P; 4 int N,n,m; 5 6 int main() 7 { 8 scanf("%d",&P); 9 while(P--){ 10 scanf("%d%d%d",&N,&n,&m); 11 printf("%d %d\n",N,1+(n-m)*m); 12 } 13 return 0; 14 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号