RealWorld Games Look Like Spinning Tops

发表时间：2020（NeurIPS 2020）
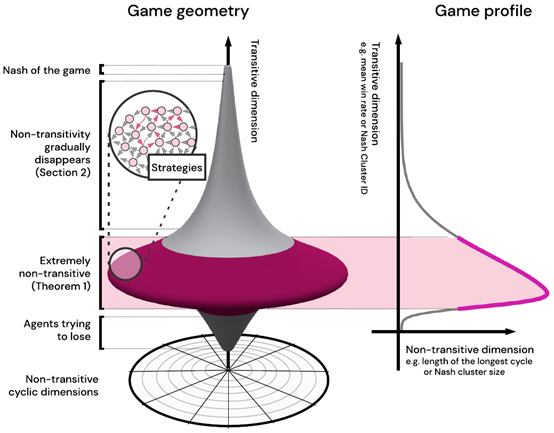
文章要点：这篇文章对博弈问题的策略空间的结构做了分析（主要还是针对two-player zero-sum symmetric games），提出策略空间是一个陀螺形状（作者把这个叫做the geometry of Games of Skill），然后就来分析需要什么条件才能找到最优解，主要解释了两个问题，clarifies why populations of strategies are necessary和how population size relates to the structure of the game,这两个问题相当于就回答了为啥要用population based的方法来训练alphastar/DOTA，以及什么情况下可以训出来。如上图所示，这个螺旋形状是个立体图，但是只有两个维度，纵轴表示transitive dimension，这个transitive不太好翻译，我理解的意思就是我的策略随着训练的过程，可以沿着这个维度往上提升/转移（transitive）。从这个维度来看，位于上面的策略一定能打过所有下面的策略，就是说有绝对的克制关系。而横轴表示non-transitive dimension，这个维度就是一个圆盘，这个圆盘上的策略都属于同一个transitive dimension，他们能打败处在他们圆盘下方的所有策略，但是在这个圆盘上的策略之间没有绝对的克制关系，而是会出现石头剪刀布那样的循环（cyclic）克制。我们再观察一下这个陀螺的形状，他上面和下面的圆盘都比较小，中间的圆盘很大，这说明最好的策略和最坏的策略都不多，大部分策略都集中在中间的位置，这说明中间位置的策略很多都是有循环克制关系的。有个问题就是如何从这些具有循环克制关系的策略中脱颖而出，transit到上面的策略中去呢？Theorem 3.说明了需要满足的条件

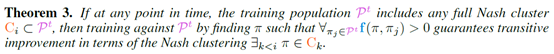
大概意思是说，如果想从这一层圆盘里跳到更上层去，只需要这一层的圆盘里的策略包含所有的循环克制关系，然后针对这些策略训练一个可以打败所有这些策略的新策略，那这个新策略就一定跳出这个圆盘，跑到上面去了（guarantees transitive improvement）。这个逻辑还是很简单的，相当于我们首先有了各种丰富多样的策略，然后打败这些策略就好了，那必然就比这些策略都厉害了。知道这点后，再结合陀螺的形状，可以理解为啥训练到一定程度之后，想要再训练出更厉害的策略变的很难。因为中间部分的圆盘太大了，需要先有各种各样丰富的策略充满这个空间，才能得到更强的策略，否则就会陷入cycle。但通常的问题是，如何先得到这些丰富的策略呢？这个问题就很宽泛了，比如做reward shaping，比如alphastar里面的exploiters等等。而一旦越过了这个最大的圆盘，上面的圆盘就越来越小，相当于所需要的策略就越来越少，那么策略提升的速度就变快了。
总结：这paper里的图画的是真的牛皮。文章大意还是很清楚的，虽然不能直接告诉你该怎么做，但是还是从直觉上帮你理解了博弈问题的难点。里面还提了一些概念，比如n-bit communicative games，用来度量博弈的复杂度，n-bit他解释的是到游戏结束前，你能发给对手的信息总量，包括你的动作之类的，我们就直接理解成一个统计动作空间和状态空间大小的一个指标就行。再比如k-layered finite Game of Skill，这一个layer你就看成一个圆盘就行。还有什么Nash clustering这些，我也不懂。总的来说，很有意思的一篇文章，可以给你很多直觉性的理解。
疑问：好多概念都不清不楚的，博弈的知识不够用啊。Proposition 3 断句都断不对，不知所云。RPP（relative population performance）不知道是啥。Nash equilibrium will never contain a fully dominated strategy这句话怎么理解？附录的证明扫过去的，没细看。

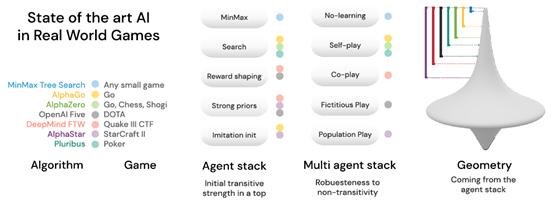
看最右边这个图，alphazero从0开始学的，为啥策略一上来就在陀螺的上面？alphastar还有人类数据做监督，为啥覆盖的范围还要更大？还是说理解错了？