台大林轩田老师《机器学习基石》课程笔记3:How can machines learn?
3 How can machines learn?
3.1 Linear Regresssion
3.1.1 算法
约定:共m个样本,\(x^{(i)}_j\)表示第i个样本中第j个特征,将各样本\(x^{(i)}\)横卧堆积形成X,即横向索引为各样本,纵向索引为各特征,维度为m*(d+1)。y和w均为向量,w维度为d+1。
则代价函数\(J(w) = \dfrac{1}{2m}\sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2 = \dfrac{1}{2m}\sum_{i=1}^m(w^T x^{(i)} - y^{(i)})^2\)
则w各分量的梯度为\(\dfrac{\partial J}{\partial w_j} = \dfrac{1}{m} \sum_{i=1}^m (w^T x^{(i)} - y^{(i)}) x^{(i)}_j\)
整理成矢量表达为\(\dfrac{\partial J}{\partial w} = \dfrac{1}{m} X^T (Xw - y)\)
方法1:梯度下降法(Ng视频方法)\(w \leftarrow w - \alpha \dfrac{\partial J}{\partial w}\)
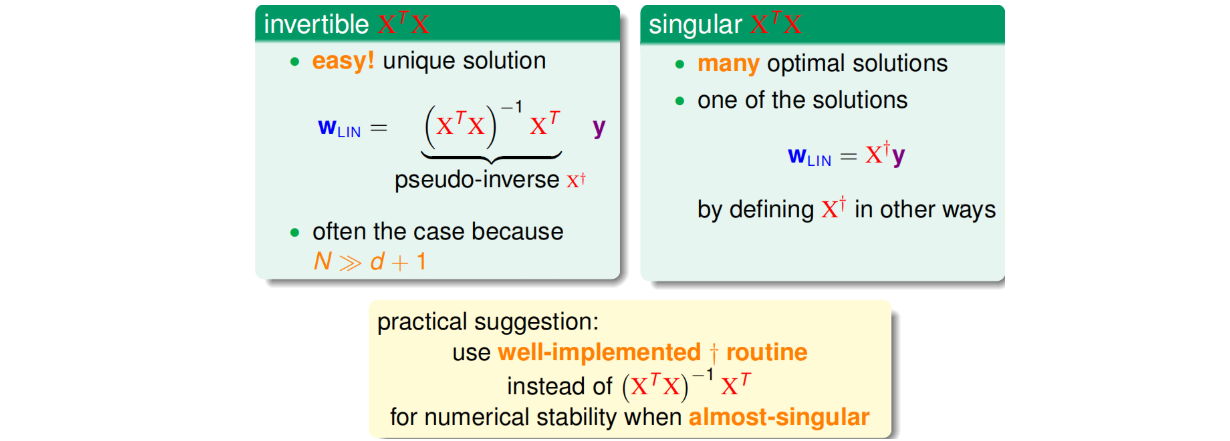
方法2:正规方程法(Normal Equation,林轩田视频方法):\(w = (X^T X)^{-1} X^T y\)
-
注意到,伪逆矩阵中有逆矩阵的计算,逆矩阵是否一定存在?一般情况下,只要满足样本数量N远大于样本特征维度d+1,就能保证矩阵的逆是存在的,称之为非奇异矩阵。但是如果是奇异矩阵,不可逆怎么办呢?其实,大部分的计算逆矩阵的软件程序,都可以处理这个问题,也会计算出一个逆矩阵。所以,一般伪逆矩阵是可解的。
![]()
-
梯度下降法和正规方程法优缺点。
3.1.2 泛化误差相关
正规方程法泛化误差:\(E_{out}≈E_{out}+ \dfrac{2(d+1)}{N}\)
linear regressin这种方法可以用在binary classification上,虽然上界变宽松了,但是仍然能得到不错的学习方法。
3.2 Logistic Regression
3.2.1 问题
一个心脏病预测的问题:根据患者的年龄、血压、体重等信息,来预测患者是否会有心脏病。很明显这是一个二分类问题,其输出y只有{-1,1}两种情况。二元分类,一般情况下,理想的目标函数f(x)>0.5,则判断为正类1;若f(x)<0.5,则判断为负类-1。
但是,如果我们想知道的不是患者有没有心脏病,而是到底患者有多大的几率是心脏病。这表示,我们更关心的是目标函数的值(分布在0,1之间),表示是正类的概率(正类表示是心脏病)。这跟我们原来讨论的二分类问题不太一样,我们把这个问题称为软性二分类问题('soft' binary classification)。这个值越接近1,表示正类的可能性越大;越接近0,表示负类的可能性越大。注意:PLA中样本标签为{+1, -1},此处标签用{0, 1}。
对于软性二分类问题,理想的数据是分布在[0,1]之间的具体值,但是实际中的数据只可能是0或者1,我们可以把实际中的数据看成是理想数据加上了噪声的影响(???)。故目标函数f: P(1|x),即正样本发生的概率值。将加权平均经过sigmoid函数转到(0,1)区间。
3.2.2 代价函数
Logistic Regression采用极大似然估计求未知参数。
使似然函数最大的假设函数h即可选为g,即\(g = \mathop{argmax}\limits_h Likelihold(h)\)
又知:记目标函数f: P(1|x)为p,则
该函数可统一为一个等式:$$P(y|x) = py(1-p), \quad y=0,1$$
故可得(注:为看得清楚,最后一行上标省略):$$\begin{equation}\begin{aligned}
g &= \mathop{argmax}\limits_h Likelihold(h)\
&= \mathop{argmax}\limits_h \sum\limits_{i=1}^m ln(P(y^{(i)} | x^{(i)})) \
&= \mathop{argmax}\limits_h \sum\limits_{i=1}^m [ylnp+(1-y)ln(1-p)] \
&= \mathop{argmin}\limits_h -\sum\limits_{i=1}^m [ylnp+(1-y)ln(1-p)]
\end{aligned}\end{equation}$$
即为Ng视频中代价函数(也称为cross-entropy error交叉熵误差):
代价函数采用梯度下降法求解,过程略。
20190920注:林课中假设负样本为\(y=-1\),故\(h(x_n)\)和\(1-h(x_n)\)均可以写成\(h(y_n x_n)\)的形式,即可推出\(err(w,x_n,y_n)=ln(1+e^{-y_n w^T x_n})\),也称为cross-entropy error,推导详情可参考笔记。
3.2.3 Perceptron与Logistic Regression区别与联系

3.3 Linear Models for Classification
3.3.1 Linear Models for Binary Classification
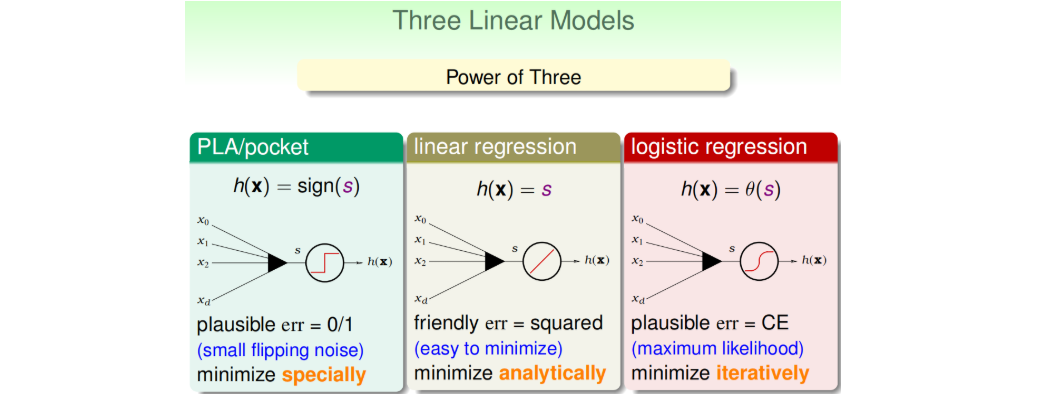
三种线性模型:
- 第一种是linear classification,err是0/1的,所以对应的\(E_{in}(w)\)是离散的,并不好解,这是个NP-hard问题;
- 第二种是linear regression,err是squared的,所以对应的\(E_{in}(w)\)是开口向上的二次曲线,其解是closed-form的,直接用线性最小二乘法求解即可,或者GD法;
- 第三种是logistic regression,err是cross-entropy的,所有对应的\(E_{in}(w)\)是平滑的凸函数,可以使用梯度下降算法求最小值。
注意:该课程中linear classification与logistic regression不同,前者特指结果只有两种{+1,-1},后者特指结果为概率值(0,1)。(想法:后者之所以叫regression,拟合的是概率的regression,分类功能是下一步的副产品。)
三种线性模型均使用了线性得分函数\(s=w^Tx\),均可用于解决linear classification的问题,优缺点如下。通常,我们使用linear regression来获得初始化的\(w_0\),再用logistic regression模型进行最优化解。
3.3.2 Multiclass Classification
针对多元分类问题,有三种解决方案:
(1).采用一对多、linear classification的方式;
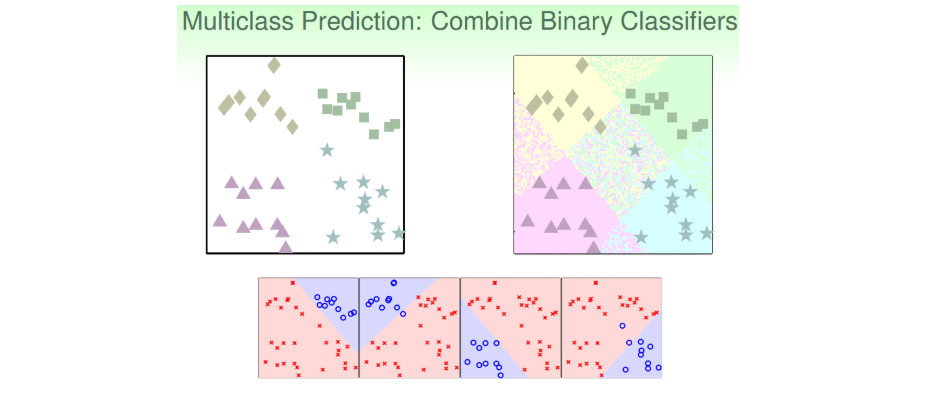
- 先把正方形作为正类,其他三种形状都是负类,即把它当成一个二分类问题,通过linear classification模型进行训练,得出平面上某个图形是不是正方形,且只有{-1,+1}两种情况。然后再分别以菱形、三角形、星形为正类,进行二元分类。这样进行四次二分类之后,就完成了这个多分类问题。
- 带来的问题:因为我们只用{-1,+1}两个值来标记,那么平面上某些可能某些区域都被上述四次二分类模型判断为负类,即不属于四类中的任何一类;也可能会出现某些区域同时被两个类甚至多个类同时判断为正类,比如某个区域又判定为正方形又判定为菱形。那么对于这种情况,我们就无法进行多类别的准确判断,所以对于多类别,简单的binary classification不能解决问题。
(2).采用一对多、logistic regression的方式(称为One-Versus-All(OVA) Decomposition);
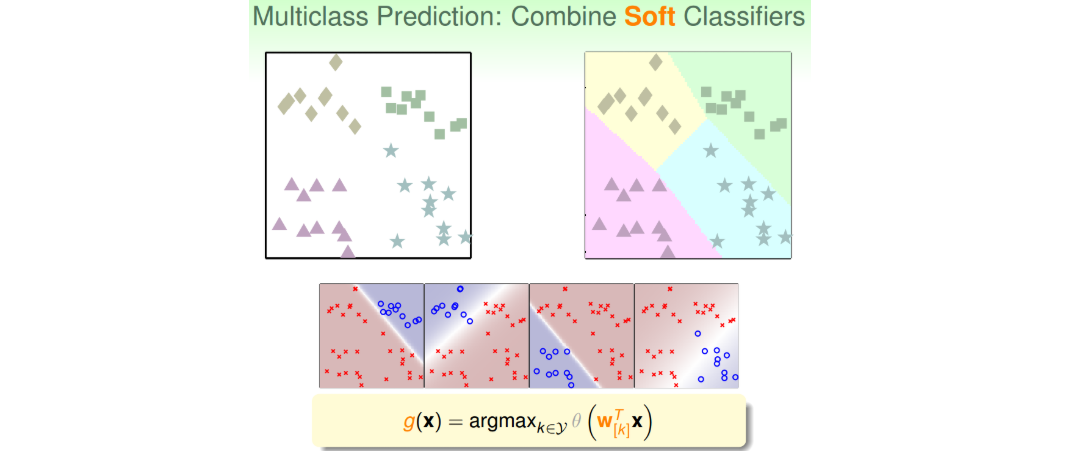
- 针对方案1的问题,可以使用另外一种方法来解决:soft软性分类,即不用{-1,+1}这种binary classification,而是使用logistic regression,计算某点属于某类的概率、可能性,取概率最大的值为那一类即可。
- 优点:简单高效,可以使用logistic regression模型来解决;缺点是如果数据类别很多时,那么每次二分类问题中,正类和负类的数量差别就很大,数据不平衡unbalanced,这样会影响分类效果。
(3).采用一对一、Binary Classification的方式(称为One-Versus-One(OVO) Decomposition);
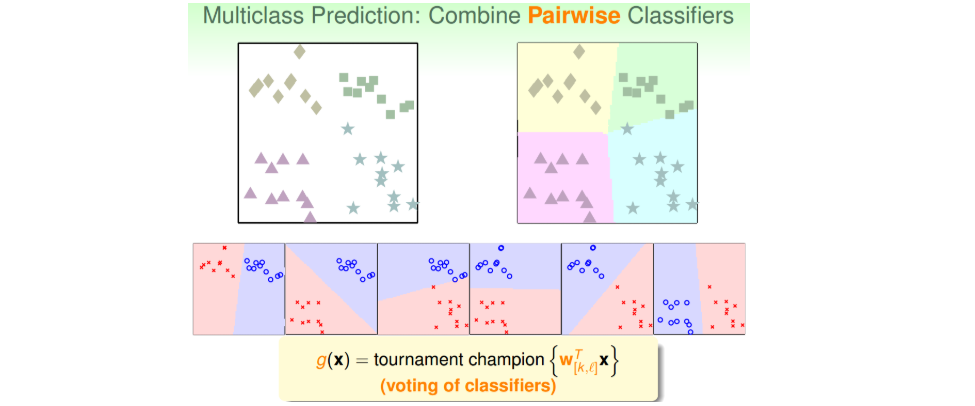
- 这种方法每次只取两类进行binary classification,取值为{-1,+1}。假如k=4,那么总共需要进行\(C_4^2=6\)次binary classification。那么,六次分类之后,如果平面有个点,有三个分类器判断它是正方形,一个分类器判断是菱形,另外两个判断是三角形,那么取最多的那个,即判断它属于正方形,完成分类。这种形式就如同k个足球对进行单循环的比赛,每场比赛都有一个队赢,一个队输,赢了得1分,输了得0分。那么总共进行了\(C_k^2\)次的比赛,最终取得分最高的那个队。
- 优点:解决了类别较多带来的数据不平衡问题,且更加高效,因为虽然需要进行的分类次数增加了,但是每次只需要进行两个类别的比较,也就是说单次分类的数量减少了;缺点是需要分类的次数多,时间复杂度和空间复杂度可能都比较高。
注意:
- 根据情况,主要用后两种;
- 方案2中Log_R可用其他软分类器代替;方案3类似,能进行binary classification的均可;
- 也可能出现OVO比OVA时间复杂度小的情况,比如fun例题。
3.4 Nonlinear transformation
上一节主要了解了三种线性模型可以用于解决binary classification和multiclass classification问题,这一节介绍:利用非线性变换解决非线性分类问题;非线性变换带来的问题;如何安全地使用非线性变换。
3.4.1 Nonlinear transform
线性模型的优点就是,它的VC Dimension比较小,保证了\(E_{in}\approx E_{out}\)。但是缺点也很明显,对某些非线性问题,可能会造成\(E_{in}\)很大,虽然\(E_{in}\approx E_{out}\),但是也造成\(E_{out}\)很大,分类效果不佳。
一种解决方式是,将低维的特征映射到高维空间中,从而将低维空间中非线性问题转化高维空间中的线性问题。比如多项式回归,将各项变量作为一个维度。基于这种非线性思想,我们之前讨论的PLA、Regression问题都可以有非线性的形式进行求解。我们把\(x_n\rightarrow z_n\)这个过程称之为特征转换(Feature Transform)。

注意:
- 目前讨论的x域中的圆形都是圆心过原点的,对于圆心不过原点的一般情况,\(x_n\rightarrow z_n\)映射公式包含的所有项为:\(\Phi_2(x)=(1,x_1,x_2,x_1^2,x_1x_2,x_2^2)\)
- 已知x域中圆形可分在z域中是线性可分的,那么反过来,如果在z域中线性可分,是否在x域中一定是圆形可分的呢?答案是否定的。由于权重向量w取值不同,x域中的hypothesis可能是圆形、椭圆、双曲线等等多种情况,甚至在x域中不存在。即x域中特征只能映射到z域中一部分空间(另一部分是复数域映射过来的?)。

整个过程就是通过映射关系,换个空间去做线性分类,重点包括两个:特征转换;训练线性模型。之后预测时也进行变换至z域中判断。
3.4.2 Price of Nonlinear Transform
进行特征变换之后,z域维度为\(d_z = C_{Q+d}^Q = C_{Q+d}^Q = O(Q^d)\) ,其中Q为多项式次数,d为x域维度。可以看出,随着Q和d的增大,z域维度急剧增加。(思考:是否因为引入了大量冗余信息?比如\(x\)、\(x^2\)本来是相关的,但在z域中纯粹作为两个独立维度。)
z域维度急剧增加带来了三个问题:
- 计算和存储空间过大;
- \(d_{VC}\)增大导致泛化误差变大;
- 若以\(\Phi_Q(x)\)表示对x域的Q次特征变换,则可以看出\(E_{in}(g)\)逐渐减小,而\(d_{VC}\)逐渐增大。
- \(d_{VC}\)增大,能降低\(E_{in}(g)\),但对\(E_{out}(g) = E_{in}(g)\)的保证越来越弱。故\(E_{out}(g)\)可能先减小后增大。
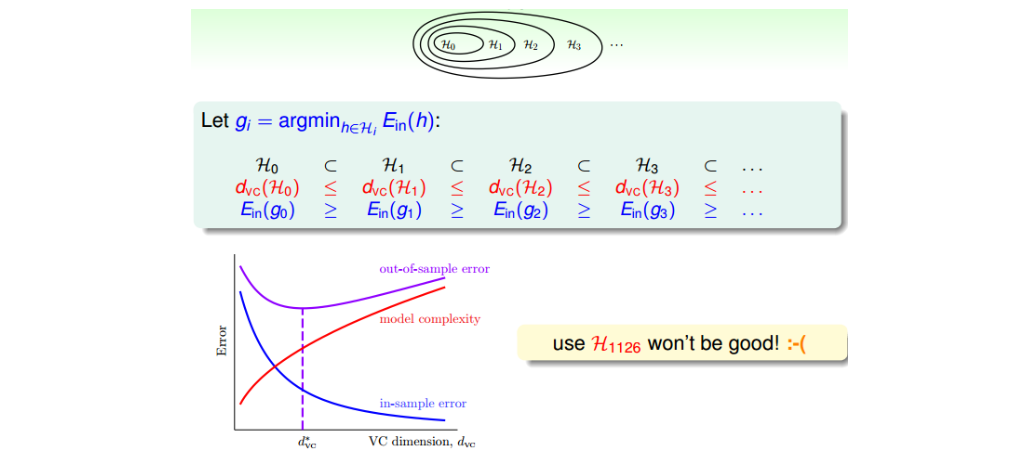
- 数据量可能不再够用。
解决方案:如何选择合适的Q,来保证不会出现过拟合问题,使模型的泛化能力强呢?
- 一般情况下,为了尽量减少特征自由度,我们会根据训练样本的分布情况,人为地减少、省略一些项。但是,这种人为地删减特征会带来一些“自我分析”代价,虽然对训练样本分类效果好,但是对训练样本外的样本,不一定效果好。所以,一般情况下,还是要保存所有的多项式特征,避免对训练样本的人为选择。
- 使用非线性变换的最安全的做法,尽可能使用简单的模型,而不是模型越复杂越好。通常情况下线性模型就可以解决很多问题。实在不行时再往右边挪。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号