三种最短路径的模板

1.迪杰斯特拉(dijkstra)：

（1）朴素版：

void dijkstra()
{
    int g,minx; 
    z[s]=1;//起点标记 
    for(int i=1;i<=n;i++)//初始化 
    {
        dist[i]=v[s][i];
    }
    for(int i=1;i<=n;i++)//n个节点，找n次 
    {
        minx=INT_MAX;
        for(int j=1;j<=n;j++)
        {
            if(!z[j]&&(dist[j]<minx))//寻找未被标记的最小节点 
            {
                minx=dist[j];
                g=j;
            }
         }
         z[g]=1;//标记被找到的最小节点
         for(int k=1;k<=n;k++) 
         {
             if(!z[k]&&dist[k]>(dist[g]+v[g][k]))//更新节点(s->k大于s->g->k)
             {
                 dist[k]=dist[g]+v[g][k];
             }
         }
    }
 } 

（2）邻接表存图+优先队列优化

void dijkstra()
{
    //初始化 
    fill(dis,dis+maxn,inf);
    dis[s]=0;
    q.push(make_pair(0,s));//第一维存储dis的相反数：把大根堆转化为小根堆 
    //直到队列为空，没有更短路径 
    while(!q.empty)
    {
        //获取队头元素，有push就有pop 
        int x=q.top().second;
        q.pop();
        //是否以及添加进图中 
        if(vis[x]==1)
        continue;
        vis[x]=1;//添加 
        //松弛操作，基于终点 
        for(int i=head[x];i!=0;i=edge[i].next)
        {
            int to=edge[i].to;
            if(!vis[to]&&dis[to]>dis[x]+edge[i].dis)
            {
                dis[to]=dis[x]+edge[i].dis;
                //入队 
                q.push(make_pair(-dis[to],to)); 
            }
        }
    }
 } 

2.贝尔曼福特(bellman_ford)：

（1）朴素+优化：

void bellman_ford()
{
    //初始化 
    fill(dis,dis+maxn,inf);
    dis[s]=0; 
    //核心：两层循环 
    for(int i=1;i<=n-1;i++)
    {
        check=0; 
        for(int j=1;j<=m;j++)
        {
            //松弛操作，基于起点 
            if(dis[u[i]]!=inf&&dis[v[i]]>dis[u[i]]+w[i])
            {
                dis[v[i]]=dis[u[i]]+w[i];
                check=1;
            }
        }
        //如果没有进行新的松弛操作，说明已经是最短路径，结束循环便可 
        if(check==0)
        break;
    }
    //判断是否有负权回路 
    for(int i=1;i<=n-1;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(dis[v[i]]>dis[u[i]]+w[i])
            {
                flag=1;
                break;
            }
        }
    }
    //输出 
    if(flag==0)
    {
        //输出最短路径 
     } 
     else
     //有负权回路 
 } 

（2）队列优化，邻接表存图：

//first[],next[],u[],v[],w[]：邻接表
//book标记是否在队列中 
void bellman_ford()
{
    //初始化 
    fill(dis,dis+maxn,inf);
    dis[s]=0;
    book[s]=1;
    q.push(s);
    //循环，队列不为空
    while(!q.empty())
    {
        //取队头 
        int k=first[q.front()];
        //取的顶点在已有范围内 
        while(k!=-1)
        {
            //松弛操作 
            if(dis[v[k]]>dis[u[k]]+w[k])
            {
                dis[v[k]]=dis[u[k]]+w[k];
            //顶点v[k]不在队列中，则加入到队列并标记 
            if(book[v[k]]==0)
            {
                q.push(k[v]);
                book[v[k]]=1;
            }
            }
            //取下一个k，链表结构 
            k=next[k];
        }
        //出队 
        q.pop();
    }
}

3.弗洛伊德算法（floyed）:

//基于已有的矩阵 
void floyed()
{
    //初始化 
    cin>>n>>m; 
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            //初始化矩阵对角线为0 
            if(i==j)
            dis[i][j]=0;
            else
            dis[i][j]=inf;
        }
     } 
     for(int i=1;i<=m;i++)
     {
         cin>>u>>v>>w;
         dis[u][v]=w;
     }
     //核心，三个循环，5行 
     for(int k=1;k<=n;k++)
     {
         for(int i=1;i<=n;i++)
         {
             for(int j=1;j<=n;j++)
             {
                 if(dis[i][j]>dis[i][k]+dis[k][j])
                 {
                     dis[i][j]=dis[i][k]+dis[k][j];
                 }
             }
         }
     }
}

三种算法的时间，空间复杂度以及适用情况

 

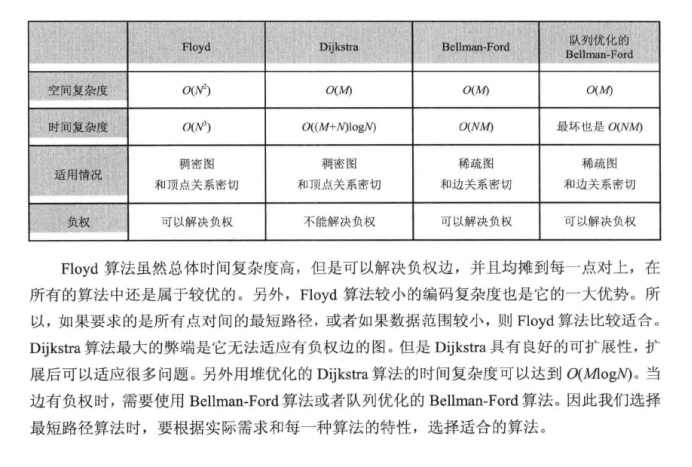
 ——《啊哈！算法》