第一次小组作业（四则运算）

项目成员及项目地址

成员1姓名	何昊天	学号	3123004481
成员2姓名	王佳俊	学号	3123004496
github:https://github.com/YezhuT0nyS/3123004481sizeyunsuan

一、PSP表格
PSP Personal Software Process Stages 预估耗时（分钟） 实际耗时（分钟）
Planning 计划 10 20
· Estimate · 估计这个任务需要多少时间 10 20
Development 开发 460 590
· Analysis · 需求分析 (包括学习新技术) 90 120
· Design Spec · 生成设计文档 25 30
· Design Review · 设计复审 20 20
· Coding Standard · 代码规范 (为目前的开发制定合适的规范) 15 30
· Design · 具体设计 50 80
· Coding · 具体编码 180 190
· Code Review · 代码复审 20 30
· Test · 测试（自我测试，修改代码，提交修改） 60 90
Reporting 报告 170 190
· Test Repor · 测试报告 60 90
· Size Measurement · 计算工作量 10 15
· Postmortem & Process Improvement Plan · 事后总结, 并提出过程改进计划 100 80
· 合计 640 790

2 效能分析
2.1 初始性能分析图：

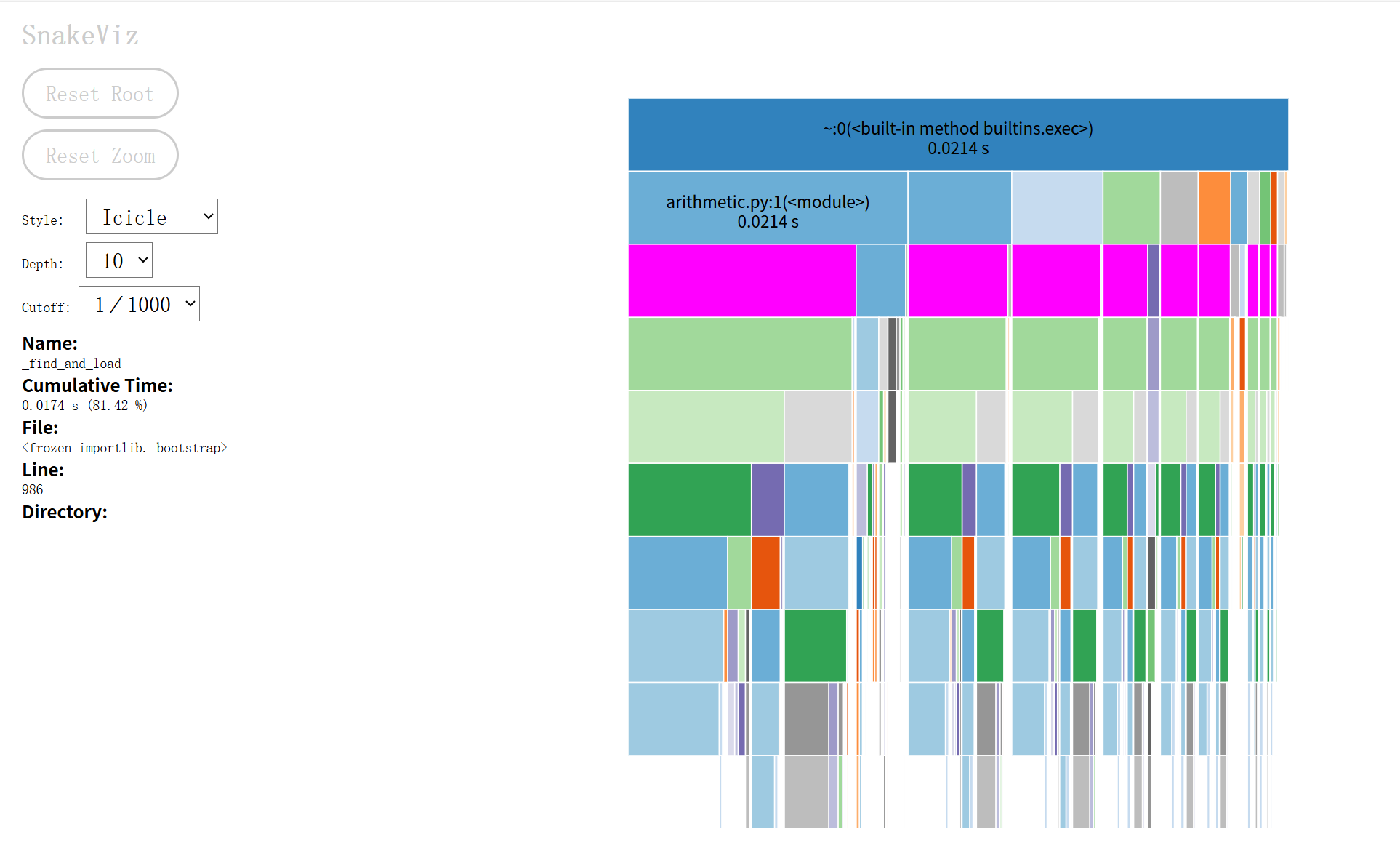
最耗时函数：generate_expression

def generate_expression(operator_count, range_limit):
"""生成一个表达式"""
if operator_count == 0:
# 生成一个数字作为表达式
num = generate_number(range_limit)
return Expression(str(num), num)

# 随机选择运算符
op = random.choice(['+', '-', '×', '÷'])

# 分配运算符给左右子表达式
left_ops = random.randint(0, operator_count - 1)
right_ops = operator_count - 1 - left_ops

# 生成左右子表达式
left_expr = generate_expression(left_ops, range_limit)
right_expr = generate_expression(right_ops, range_limit)

# 根据运算符计算结果并验证
result = None
if op == '+':
    result = left_expr.value + right_expr.value
elif op == '-':
    result = left_expr.value - right_expr.value
    # 确保减法结果非负
    if result is None:
        return None
elif op == '×':
    result = left_expr.value * right_expr.value
elif op == '÷':
    # 确保除法结果为真分数
    result = left_expr.value / right_expr.value
    if result is None:
        return None

# 随机决定是否添加括号
add_parentheses = random.random() < 0.3
left_str = f"({left_expr.expr_str})" if add_parentheses and left_ops > 0 else left_expr.expr_str
add_parentheses = random.random() < 0.3
right_str = f"({right_expr.expr_str})" if add_parentheses and right_ops > 0 else right_expr.expr_str

# 构建表达式字符串
expr_str = f"{left_str} {op} {right_str}"
return Expression(expr_str, result)

性能瓶颈分析：
1、无效重试过多函数在生成减法（e1 - e2）和除法（e1 ÷ e2）表达式时，需要满足 e1 ≥ e2（减法）和 结果为真分数（除法）的条件。当条件不满足时，会直接返回 None 并触发重试。在数值范围较小（如 r=1 或 r=2）时，无效重试会急剧增加，导致生成效率骤降。
2、函数采用递归方式生成表达式，每次随机分配左右子表达式的运算符数量（left_ops 和 right_ops）。当运算符数量较多时，递归深度增加，且可能出现子表达式结构重复，间接导致去重阶段的 normalize_expression 函数负担加重。

改进思路：
预校验运算可行性：在生成 e1 和 e2 后，先判断运算是否可能有效，再决定是否执行运算。
减法：先生成 e1，再生成 ≤ e1 的 e2（而非随机生成后再判断）。
除法：先生成 e2，再生成 e1 为 e2 的倍数或分数（确保结果为真分数）。

优化：
def generate_expression(operator_count, range_limit):
"""生成一个表达式，确保返回有效结果"""
if operator_count == 0:
# 生成一个数字作为表达式
num = generate_number(range_limit)
return Expression(str(num), num)

# 循环直到生成有效的表达式
while True:
    # 随机选择运算符
    op = random.choice(['+', '-', '×', '÷'])

    
    # 分配运算符给左右子表达式
    left_ops = random.randint(0, operator_count - 1)
    right_ops = operator_count - 1 - left_ops
    
    # 生成左右子表达式（递归）
    left_expr = generate_expression(left_ops, range_limit)
    right_expr = generate_expression(right_ops, range_limit)
    
    # 检查子表达式是否有效
    if left_expr is None or right_expr is None:
        continue
    
    # 根据运算符计算结果并验证
    result = None
    if op == '+':
        result = left_expr.value + right_expr.value
    elif op == '-':
        result = left_expr.value - right_expr.value
        # 确保减法结果非负
        if result is None:
            continue
    elif op == '×':
        result = left_expr.value * right_expr.value
    elif op == '÷':
        # 确保除法结果有效
        result = left_expr.value / right_expr.value
        if result is None:
            continue
    
    # 随机决定是否添加括号
    add_parentheses = random.random() < 0.3
    left_str = f"({left_expr.expr_str})" if add_parentheses and left_ops > 0 else left_expr.expr_str
    add_parentheses = random.random() < 0.3
    right_str = f"({right_expr.expr_str})" if add_parentheses and right_ops > 0 else right_expr.expr_str
    
    # 构建表达式字符串
    expr_str = f"{left_str} {op} {right_str}"
    return Expression(expr_str, result)

2.2 优化后性能分析图

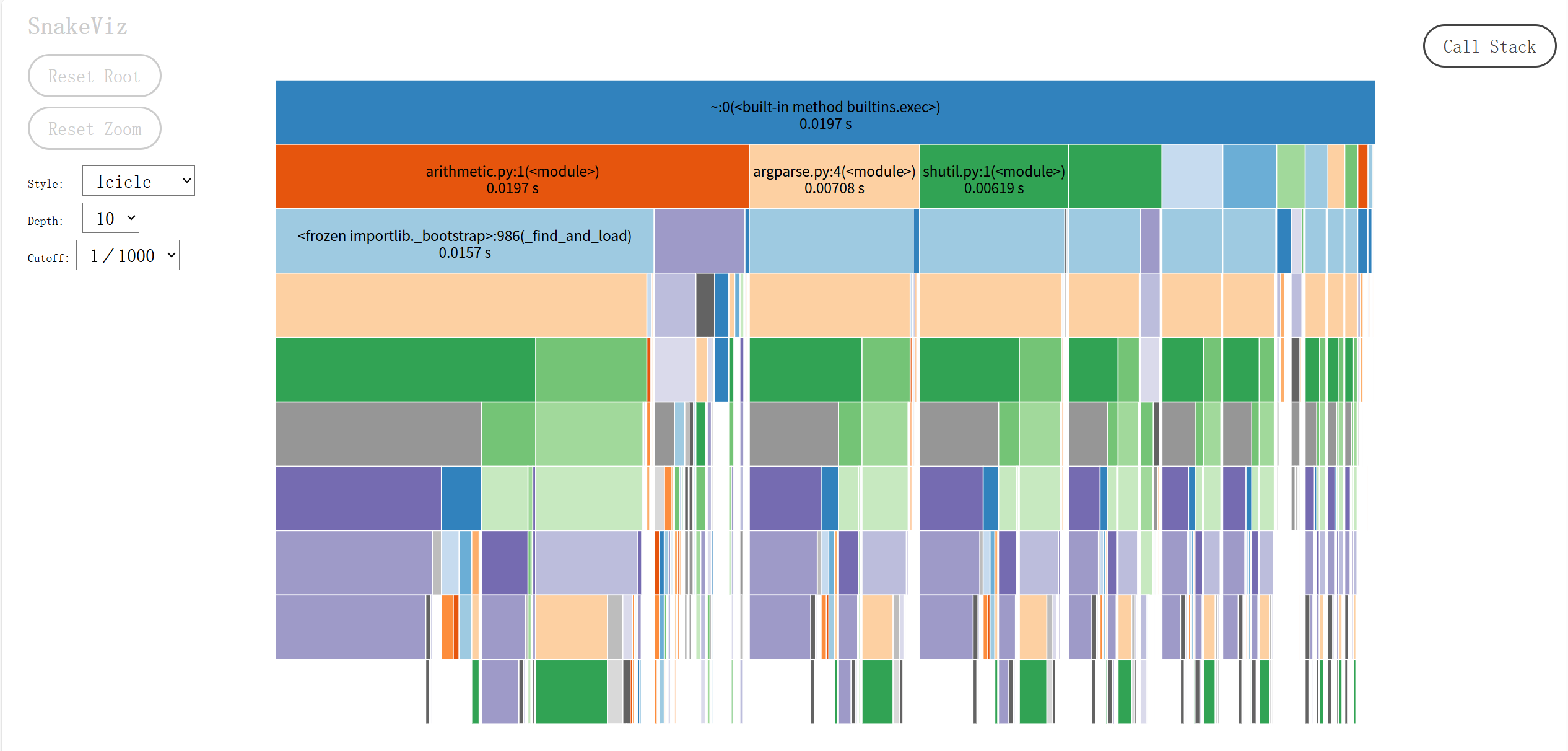
3 设计实现过程

a.基础功能：生成指定数量（-n）、指定数值范围（-r）的四则运算题，支持自然数、真分数（含带分数），运算符不超过 3 个。
b.约束条件：减法结果非负，除法结果为真分数，题目不可重复（考虑+和×的交换律）。
c.扩展功能：生成答案文件，验证用户答案并输出正确率统计。

3.1 总体流程图

5.关键代码说明

1. 分数处理类（Fraction）
   功能：封装真分数、带分数的表示、化简及四则运算，是整个程序的基础数据结构。
   关键逻辑：
   通过simlify()方法实现分数自动化简，确保存储和输出格式统一（如4/2→2，5/3→1'2/3）。
   减法和除法重载中加入约束校验，直接返回None表示运算不合法，为后续表达式生成提供判断依据。
   class Fraction:
   def init(self, numerator=0, denominator=1, integer=0):
   self.integer = integer # 带分数的整数部分（如2'3/8中的2）
   self.numerator = numerator # 分子（如3/8中的3）
   self.denominator = denominator # 分母（如3/8中的8）
   self.simplify() # 初始化时自动化简

   def simplify(self):
   """核心方法：将分数化为最简形式（自动约分、转换带分数）"""
   # 处理分母符号（确保分母为正）
   if self.denominator < 0:
   self.numerator *= -1
   self.denominator *= -1

    # 转换为假分数（便于运算）：整数部分×分母 + 分子
    total_num = self.integer * self.denominator + self.numerator
    self.integer = 0
    self.numerator = total_num
    
    # 约分（通过最大公约数GCD）
    if self.numerator != 0:
        gcd_val = math.gcd(abs(self.numerator), self.denominator)
        self.numerator //= gcd_val
        self.denominator //= gcd_val
    
    # 转换回带分数（若分子≥分母）
    if abs(self.numerator) >= self.denominator:
        self.integer = self.numerator // self.denominator  # 整数部分
        self.numerator = self.numerator % self.denominator  # 剩余分子
   

   def sub(self, other):
   """减法重载：确保结果非负（核心约束实现）"""
   # 转换为假分数计算
   num1, den1 = self.to_improper() # 自身转为假分数（分子，分母）
   num2, den2 = other.to_improper() # 另一个分数转为假分数

    new_num = num1 * den2 - num2 * den1  # 通分后相减
    new_den = den1 * den2
    
    if new_num < 0:  # 若结果为负，返回None（不合法）
        return None
    return Fraction(new_num, new_den)  # 合法则返回新分数
   

   def truediv(self, other):
   """除法重载：确保结果为真分数（核心约束实现）"""
   num1, den1 = self.to_improper()
   num2, den2 = other.to_improper()

    if num2 == 0:  # 避免除以0
        return None
        
    new_num = num1 * den2  # 被除数分子×除数分母
    new_den = den1 * num2  # 被除数分母×除数分子
    result = Fraction(new_num, new_den)
    
    # 验证结果是否为真分数（分子<分母或带分数）
    if result.integer == 0 and result.numerator >= result.denominator:
        return None  # 若为假分数且无整数部分，不合法
    return result
   

2. 表达式生成（generate_expression）
   功能：递归生成符合约束的四则运算表达式，控制运算符数量（≤3 个），避免重复。
   关键逻辑：
   采用递归策略：operator_count控制运算符数量，0 个运算符时生成单个数字，否则分解为左右子表达式 + 运算符。
   通过while True循环确保只返回合法表达式（过滤减法负数、除法非真分数的情况）。
   动态添加括号增加表达式多样性，但仅对子表达式有运算符的情况添加（避免无意义括号如(5)）。

def generate_expression(operator_count, range_limit):
"""递归生成单个表达式，确保符合减法/除法约束"""
if operator_count == 0:
# 基础情况：生成单个数字（自然数或分数）
num = generate_number(range_limit)
return Expression(str(num), num)

# 循环直到生成合法表达式
while True:
    op = random.choice(['+', '-', '×', '÷'])  # 随机选择运算符
    # 分配运算符数量给左右子表达式（如3个运算符可分为1+2）
    left_ops = random.randint(0, operator_count - 1)
    right_ops = operator_count - 1 - left_ops
    
    # 递归生成左右子表达式
    left_expr = generate_expression(left_ops, range_limit)
    right_expr = generate_expression(right_ops, range_limit)
    
    # 计算结果并验证合法性
    result = None
    if op == '+':
        result = left_expr.value + right_expr.value
    elif op == '-':
        result = left_expr.value - right_expr.value  # 可能返回None（不合法）
    elif op == '×':
        result = left_expr.value * right_expr.value
    elif op == '÷':
        result = left_expr.value / right_expr.value  # 可能返回None（不合法）
    
    if result is not None:  # 若运算合法，构建表达式并返回
        # 随机添加括号（仅当子表达式有运算符时）
        left_str = f"({left_expr.expr_str})" if left_ops > 0 and random.random() < 0.3 else left_expr.expr_str
        right_str = f"({right_expr.expr_str})" if right_ops > 0 and random.random() < 0.3 else right_expr.expr_str
        return Expression(f"{left_str} {op} {right_str}", result)

3. 题目去重（normalize_expression）
   功能：标准化表达式字符串，处理+和×的交换律导致的重复（如2+3与3+2视为重复）。

关键逻辑：
先移除冗余括号，避免(a+b)与a+b被视为不同。
对+和×运算符，递归标准化左右子表达式后按字典序排序，确保交换操作数后结果一致（如3+2→2+3）。
def normalize_expression(expr_str):
"""标准化表达式，用于去重判断"""
# 移除冗余括号（如"(a + b)" → "a + b"）
normalized = re.sub(r'(([^()]+))', r'\1', expr_str)

# 处理交换律：对+和×左右的表达式排序
for op in ['+', '×']:
    if op in normalized:
        parts = normalized.split(f' {op} ')
        if len(parts) == 2:
            # 递归标准化子部分（处理嵌套表达式）
            part1 = normalize_expression(parts[0])
            part2 = normalize_expression(parts[1])
            # 按字典序排序，确保a+b和b+a标准化后相同
            if part1 > part2:
                return f"{part2} {op} {part1}"
return normalized

5 测试运行
5.1 生成的题目与计算结果

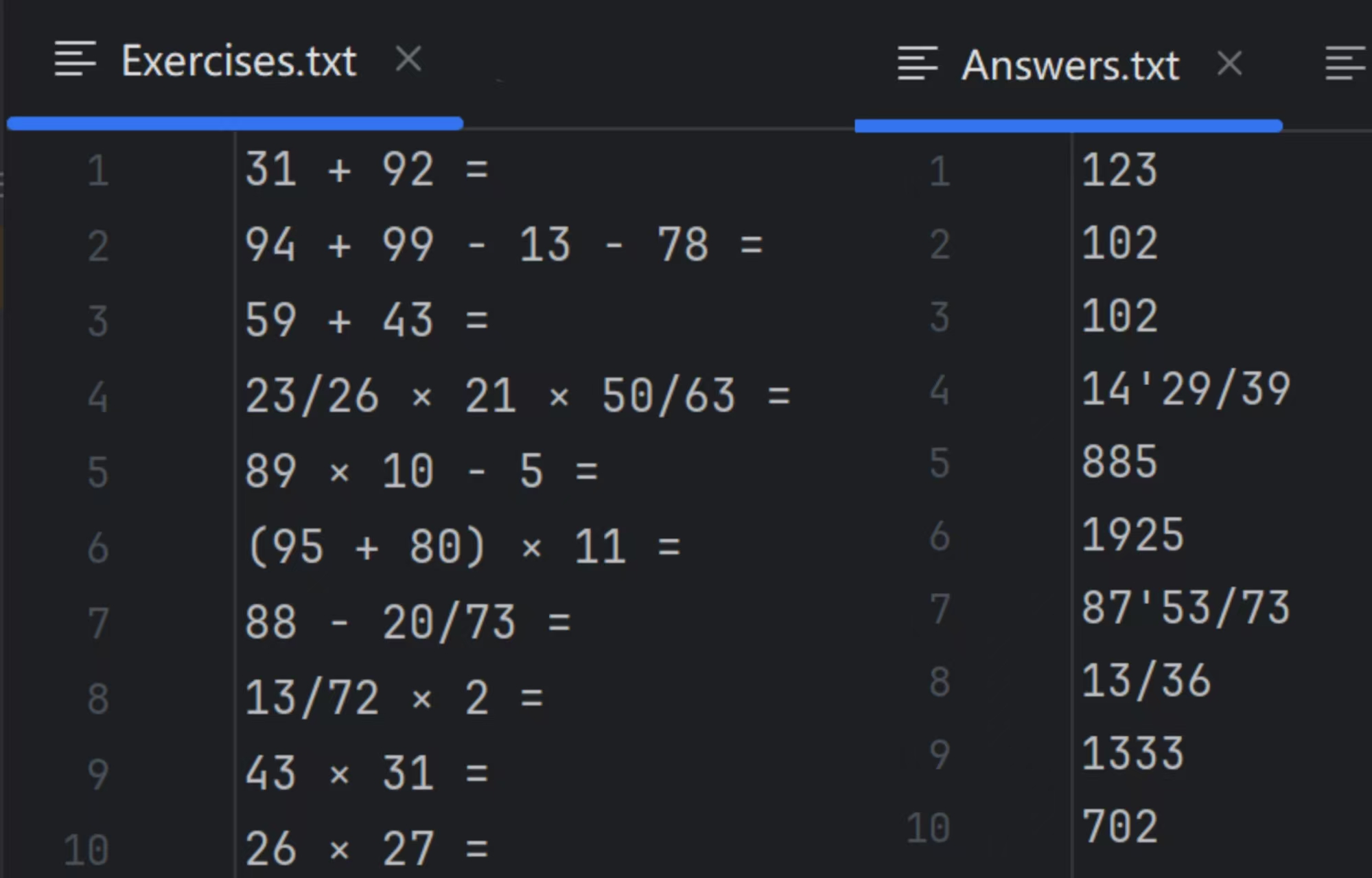
5.2 批改结果
文件grade.txt

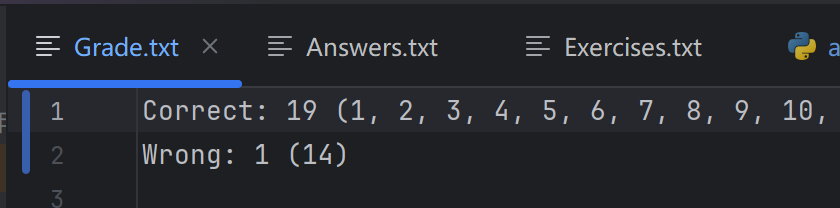
6 项目小结
刚开始面对这道四则运算程序题，看着一堆约束条件有点无从下手，光是理清题目要求就花了不少时间。后来我们决定先画总体流程图，把生成题目、验证答案的核心流程拆解开，思路一下子清晰了很多。中途代码频繁报错，从分数运算的化简问题到去重逻辑的漏洞，我们一边查CSDN案例，一边找AI辅助修改，一步步攻克了难点。

这次结对合作比单人项目轻松太多，不仅任务能分工承担，遇到卡壳时还能互相打气。特别感谢搭档的耐心与靠谱，我容易在细节上急躁，是他一直帮我梳理逻辑、提醒重点；而他在性能优化和测试上的严谨，也让程序的稳定性提升不少，尤其是去重模块的高效实现，离不开他的反复调试。

合作过程中，我们不仅解决了技术难题，更学会了沟通配合。互相分享思路、分担压力，让原本复杂的项目变得顺畅，也让我深刻感受到1+1＞2的力量，这是一次收获满满的协作经历。