宽搜BFS（Breadth-first search）和二叉树

什么时候应该使用BFS

图的遍历：

1. 层级遍历

2. 由点及面

3. 拓扑排序

最短路径：

仅限简单图（图中每条边长度都是1，且没有方向）求最短路径。

 

二叉树的基本概念
一、二叉树的概念：一棵二叉树是节点的一个有限集合，该集合或者为空，或者由一个根节点加上两棵左子树和右子树组成

二、二叉树的特点：

1、每个节点最多有两棵子树，即二叉树不存在度大于2的节点

2、二叉树的子树有左右之分，其子树的次序不能颠倒

三、二叉树的形式：

 

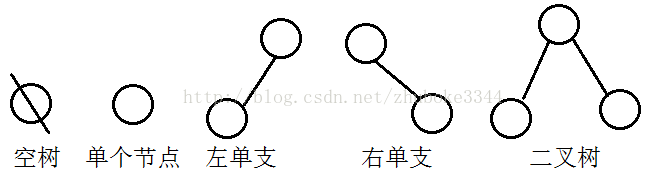
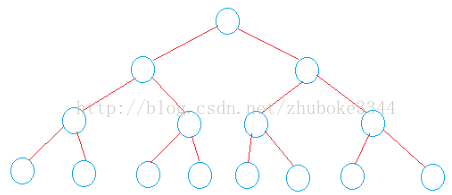
四、满二叉树：在一棵二叉树中，所有分支节点都存在左子树和右子树，并且所有的叶节点都在同一层上

 

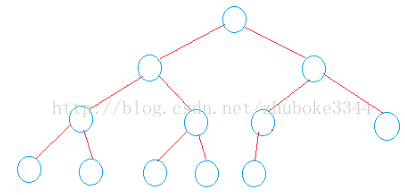
五、完全二叉树：如果一棵具有N个节点的二叉树的结构与满二叉树的前N个节点的结构相同

二叉树性质

(1) 在非空二叉树中，第i层的结点总数不超过2^(i-1), i>=1.

(2) 深度为h的二叉树最多有2^h-1个结点(h>=1)（满二叉树），最少有h个结点（单链）；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为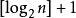（注：[ ]表示向下取整）；

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则 如果I>1，则其父结点的编号为I/2；

如果2*I<=N，则其左孩子（即左子树的根结点）的编号为2*I；若2*I>N，则无左孩子；

如果2*I+1<=N，则其右孩子的结点编号为2*I+1；若2*I+1>N，则无右孩子。