算法（第四版）C# 习题题解——3.2

写在前面

整个项目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp
查找更方便的版本见：https://alg4.ikesnowy.com/
这一节内容可能会用到的库文件有 BinarySearchTree，同样在 Github 上可以找到。
善用 Ctrl + F 查找题目。

习题&题解

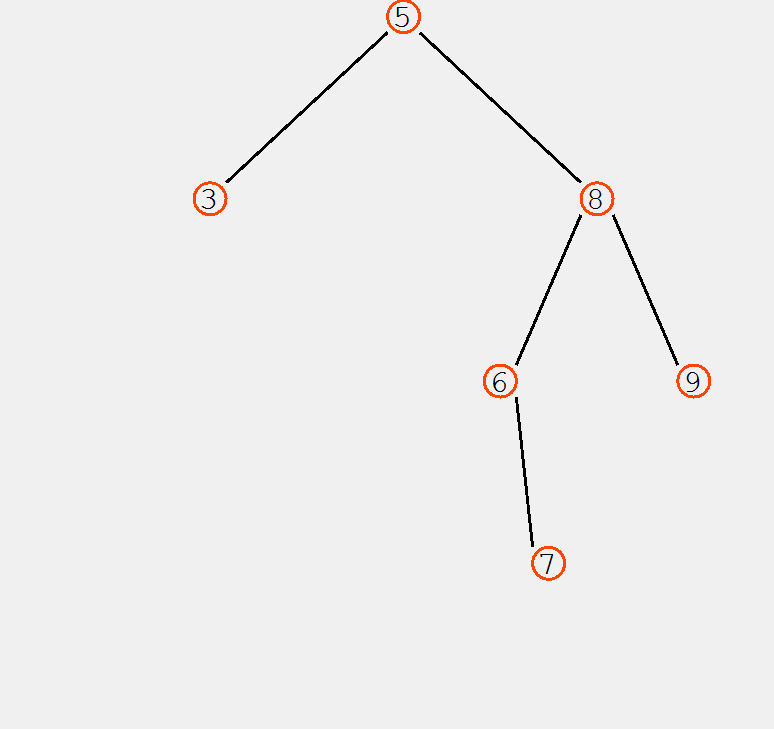
3.2.1

解答

构造出的树如下图所示：

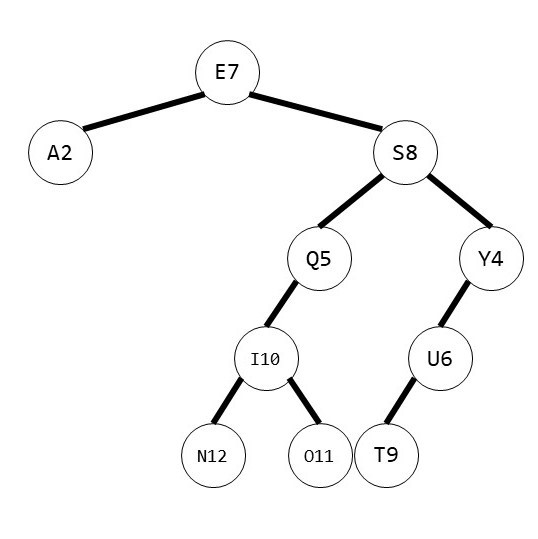
总比较次数：0 + 1 + 1 + 2 + 2 + 3 + 1 + 2 + 4 + 3 + 4 + 5 = 28 次

另请参阅

BinarySearchTree 库

3.2.2

解答

用这样的序列就可以构造出最坏情况：

"A X C S E R H",
"X A S C R E H",
"A C E H R S X",
"X S R H E C A",
"X A S R H E C",
"A X S R H E C"

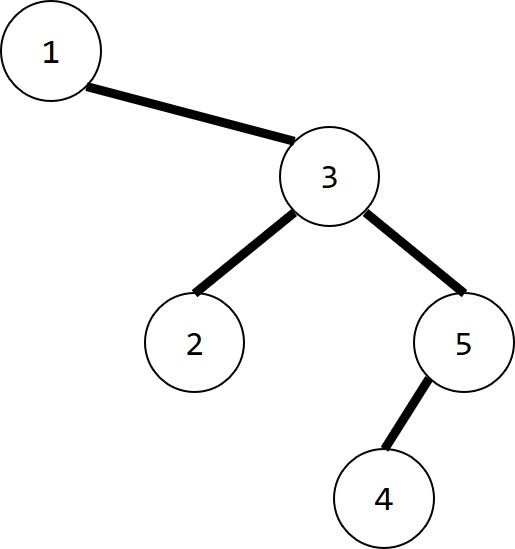
构造出来的树看起来像这样：

3.2.3

解答

官方答案：第一个插入的是 H，且 C 在 A 和 E 之前插入，S 在 R 和 X 之前插入的树。
对序列排序，得到 A C E H R S X 。
最优情况需要树两侧平衡，因此 H 为根结点，C 和 S 分别为 H 的子结点。
同理，A 和 E 为 C 的子结点，R 和 X 为 S 的子结点。

3.2.4

解答

d 是错误的。

要点是追踪序列中的左右顺序，
如果向右查找，那么后面的树一定都比它大，反之都比它小。
例如 d 选项，2->7 向右查找，但后面的 8 比 7 大，应该挂在 7 的右子树上，不可能在 7 的左子树里。

3.2.5

解答

事实上，这个问题可以归结为，如何根据频率来构造一棵最优的BST？
如果知道树的形状，逆推插入顺序也就不难了（先序遍历）。

首先我们定义某个结点的查找开销为该结点的深度加一乘以频率，
（注意根结点的深度为 0，树的高度等于整棵树中最大的深度值）
所有结点的查找开销加起来就是一整棵树的查找开销了。

\[cost(n)=\sum_{i=0}^{n} (depth(i)+1) \times frequency(i) \]

对于固定的一组键值和频率，$ cost $ 最小的树即为我们要找的树。
这样的树被称为最优化二叉树，或者 Optimal BST。

根据二叉树的性质，我们可以将 $ cost $ 的表达式变为：

\[cost(n)=cost(left)+cost(right)+\sum_{i=1}^{n} frequency(i) \]

即左子树的开销和右子树的开销相加，再加上所有结点的频率之和。
（左子树和右子树开销计算时每个结点的深度都少了1，因此要加上频率和）
不难得到结论，Optimal BST 的所有子树也都是 Optimal BST。

我们可以利用一种类似于构造哈夫曼树的方法构造 Optimal BST，
哈夫曼树中比较的是频率，而构造 Optimal BST 时比较的则是开销。
由于二叉查找树是有序的，因此我们先对序列排序。
然后计算所有大小为 1 的子树开销，显然就等于各个节点的频率。
再计算大小为 2 的子树，注意这里只能按顺序取结点，不能跳着取（例如取第一个和第三个结点），
每种结点取法都对应有两种根结点选择，计算出最小的开销并记录。
以此类推，直到计算到大小为 n 的树，此时整棵 BST 就被构造出来了。

举个例子，例如给出键值和频率如下表所示：

键值	1	2	3	4	5
频率	0.4	0.1	0.2	0.1	0.2

当 $ s=1 $ 时，各子树的开销如下表（根结点不唯一）：

子树	[1,1]	[2,2]	[3,3]	[4,4]	[5,5]
开销	0.4	0.1	0.2	0.1	0.2
根结点	1	2	3	4	5

当 $ s=2 $ 时，各个子树的开销如下（根结点不唯一）：

子树	[1,2]	[2,3]	[3,4]	[4,5]
开销	$ \min \begin{cases} 0+[2,2]+0.5, \\ [1,1]+0+0.5, \end{cases} \\ =0.6 $	$ \min \begin{cases} 0+[3,3]+0.3, \\ [2,2]+0+0.3, \end{cases} \\ =0.4 $	$ \min \begin{cases} 0+[4,4]+0.3, \\ [3,3]+0+0.3, \end{cases} \\ =0.4 $	$ \min \begin{cases} 0 +[5,5]+0.3, \\ [4,4]+0+0.3, \end{cases} \\ =0.4 $
根结点	1	3	3	5

当 $ s=3 $ 时，各个子树的开销如下表（根结点不唯一）：

子树	[1,3]	[2,4]	[3,5]
开销	$ \min \begin{cases} 0+[2,3]+0.7, \\ [1,1]+[3,3]+0.7, \\ [1,2]+0+0.7, \end{cases} \\ =1.1 $	$ \min \begin{cases} 0+[3,4]+0.4, \\ [2,2]+[4,4]+0.4, \\ [2,3]+0+0.4, \end{cases} \\ =0.6 $	$ \min \begin{cases} 0+[4,5]+0.5, \\ [3,3]+[5,5]+0.5, \\ [3,4]+0+0.5, \end{cases} \\ =0.9 $
根结点	1	3	3

当 $ s=4 $ 时，各个子树的开销如下表（根结点不唯一）：

子树	[1,4]	[2,5]
开销	$ \min \begin{cases} 0+[2,4]+0.8, \\ [1,1]+[3,4]+0.8, \\ [1,2]+[4,4]+0.8, \\ [1,3]+0+0.8, \end{cases} \\ = 1.4 $	$ \min \begin{cases} 0+[3,5]+0.5, \\ [2,2]+[4,5]+0.5, \\ [2,3]+[5,5]+0.5, \\ [2,4]+0+0.5, \end{cases} \\ = 1.0 $
根结点	1	3

当 $ s=5 $ 时，各个子树的开销如下表（根结点不唯一）：

子树	[1,5]
开销	$ \min \begin{cases} 0+[2,5]+1.0, \\ [1,1]+[3,5]+1.0, \\ [1,2]+[4,5]+1.0, \\ [1,3]+[5,5]+1.0, \\ [1,4]+0+1.0 \end{cases} \\ = 2.0 $
根结点	1

于是最优二叉树为（不唯一）：

另请参阅

Optimal Binary Search Tree - Wikipedia

3.2.6

解答

官方 BST 实现见：https://algs4.cs.princeton.edu/32bst/BST.java.html

二叉树的高度=左右子树最大高度+1，叶结点的高度为 0。
于是我们可以构造如下递归方法：

private int Height(Node x)
{
    return x == null ? -1 : 1 + Math.Max(Height(x.Left), Height(x.Right));
}

当 x 等于 null 时，说明它是叶子结点的左/右子树，应该返回 0-1=-1。

也可以在结点中添加一个 Height 属性，记录当前结点的高度，当插入新结点时重新计算高度。
在 Put 方法中添加计算高度的代码：

private Node Put(Node x, TKey key, TValue value)
{
    if (x == null)
        return new Node(key, value, 1, 0);
    int cmp = key.CompareTo(x.Key);
    if (cmp < 0)
        x.Left = Put(x.Left, key, value);
    else if (cmp > 0)
        x.Right = Put(x.Right, key, value);
    else
        x.Value = value;
    x.Size = 1 + Size(x.Left) + Size(x.Right);
    x.Height = 1 + Math.Max(Height(x.Left), Height(x.Right));
    return x;
}

由于叶结点的高度为零，因此新插入的结点高度应该初始化为 0。

3.2.7

解答

平均查找次数 = 树所有结点的深度之和 / 结点个数 + 1。

只要能够获得深度和，就能构造出如下用于计算平均查找次数的方法：

public int AverageCompares()
{
    return DepthSum(root) / Size() + 1;
}

二叉树的深度之和 = 左子树的深度和 + 右子树的深度和 + 左子树的结点个数 + 右子树的结点个数
（加上根结点会使左右子树所有结点的深度+1）

于是我们可以获得如下递归方法，用于计算一棵树的深度和：

private int DepthSum(Node x)
{
    if (x == null)
        return 0;
    return DepthSum(x.Left) + DepthSum(x.Right) + x.Size - 1;
}

也可以在结点中直接添加一个 DepthSum 属性，用于记录当前结点的深度和。
需要在每次插入新结点时重新计算查找路径上所有结点的 DepthSum。

private Node Put(Node x, TKey key, TValue value, int depth)
{
    if (x == null)
        return new Node(key, value, 1, depth);
    var cmp = key.CompareTo(x.Key);
    if (cmp < 0)
        x.Left = Put(x.Left, key, value, depth + 1);
    else if (cmp > 0)
        x.Right = Put(x.Right, key, value, depth + 1);
    else
        x.Value = value;
    x.Size = 1 + Size(x.Left) + Size(x.Right);
    x.DepthSum = depth;
    if (x.Left != null)
        x.DepthSum += x.Left.DepthSum;
    if (x.Right != null)
        x.DepthSum += x.Right.DepthSum;
    return x;
}

在插入结点时需要传入一个参数以记录当前深度，新插入结点的默认深度和就是当前深度。

3.2.8

解答

假设输入的完全二叉树结点数目为 $n$。

完全二叉树总是可以分成两部分，一个满二叉树，以及多余的结点。

于是完全二叉树中满二叉树的部分层数为 $l = \lfloor \log_2 (n+1) \rfloor$。（根结点位于第一层）
满二叉树占的结点数量为 $n_1 = 2^l -1$，多余结点数量为 $ n_2=n-n_1$。

又因为深度等于层数 - 1，多余结点正好在满二叉树的下一层，因此多余结点的深度即为 $ l $。
于是多余结点的深度和 $d_2 = l \times n_2$。

接下来计算满二叉树的深度和。
一个层数为 $ l $ 的满二叉树，最后一层正好有 $ 2^{l-1} $ 个结点。
于是深度和为 $ d_1 = 0 \times 1 + 1 \times 2+2 \times 4+\cdots+(l-1)2^{l-1} =\sum_{i=1}^{l-1} i2^i $。
用错位相减法，有：

\[\begin{eqnarray*} d_1&=&1\times 2^1 + &2 \times 2^2 + \cdots + (l-1)2^{l-1} \\ 2d_1&=& &1\times 2^2 + \cdots+(l-2)2^{l-1} +(l-1)2^{l} \\ d_1-2d_1&=& 1 \times2^1+ &1 \times2^2+\cdots+1\times2^{l-1}-(l-1)2^l \\ d_1 &=&(l-1)2^l &-2^l+2 \\ &=&(l-2)2^l &+2 \end{eqnarray*} \]

于是可得总深度和： $d=d_1+d_2=l\times n_2+ (l-2)2^l+2$。
平均查找次数即为：$avgCompare=d / n + 1$ 。

代码

private static int OptCompares(int n)
{
    // 完全二叉树 = 满二叉树 + 多余结点
    // 满二叉树的层数。
    var l = (int)Math.Log(n + 1, 2);
    // 多余结点的个数。
    var extraNodes = n + 1 - (int)Math.Pow(2, l);

    var depthSum =
        extraNodes * l + (l - 2) * (int) Math.Pow(2, l) + 2;
    return depthSum / n + 1;
}

3.2.9

解答

比较简单，可以按照如下步骤解决：

生成 n 个数。
生成这 n 个数的全排列。
生成 n! 棵二叉搜索树，取其中结构不同的部分。

全排列可以通过递归方式生成，方法类似于 DFS。
开始 pool 中存有所有的数，遍历 pool ，每次取一个数放入 path 中，然后递归选择下一个。

static void Permutation(List<int> pool, List<int> path, List<int[]> result)
{
    if (pool.Count == 0)
    {
        result.Add(path.ToArray());
        return;
    }

    for (var i = 0; i < pool.Count; i++)
    {
        var item = pool[i];
        path.Add(item);
        pool.RemoveAt(i);
        Permutation(pool, path, result);
        pool.Insert(i, item);
        path.Remove(item);
    }
}

有了 n! 棵二叉树之后，我们需要过滤掉结构相同的树。
我们可以把二叉树转换成数组表示（层序遍历即可），然后遍历数组进行比较。

var treeA = a.ToArray();
var treeB = b.ToArray();

if (treeA.Length != treeB.Length)
    return false;
for (var i = 0; i < treeA.Length; i++)
{
    if (treeA[i] == null && treeB[i] == null)
        continue;
    if (treeA[i] != null && treeB[i] != null)
        continue;
    return false;
}

return true;

结果如下：

n=2

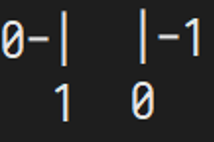
n=3

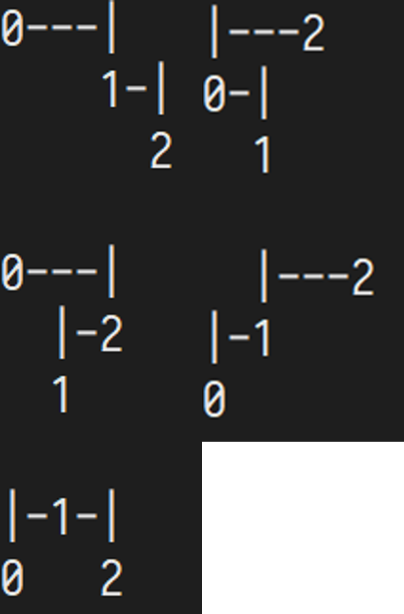
n=4

n=5

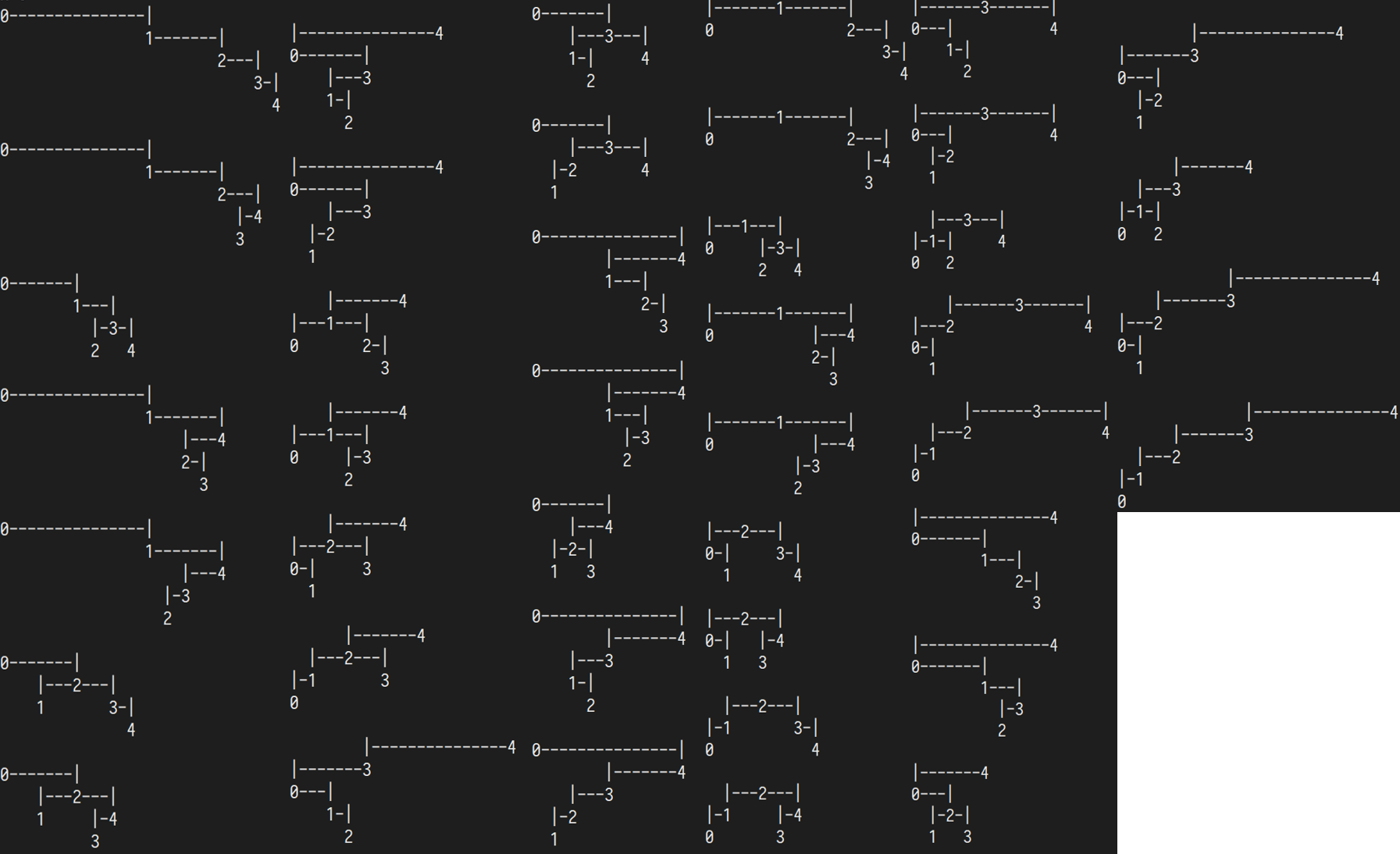
n=6

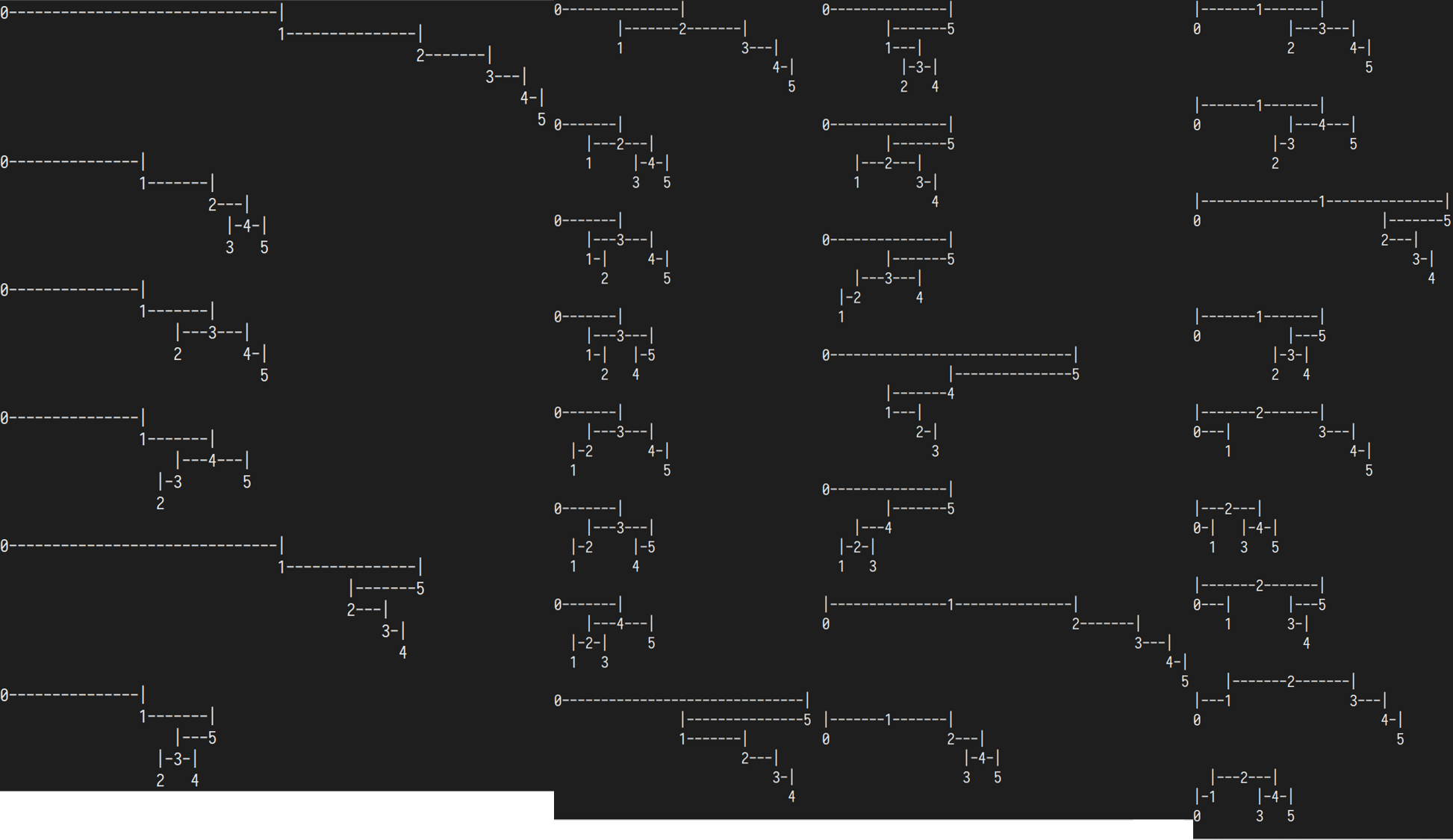
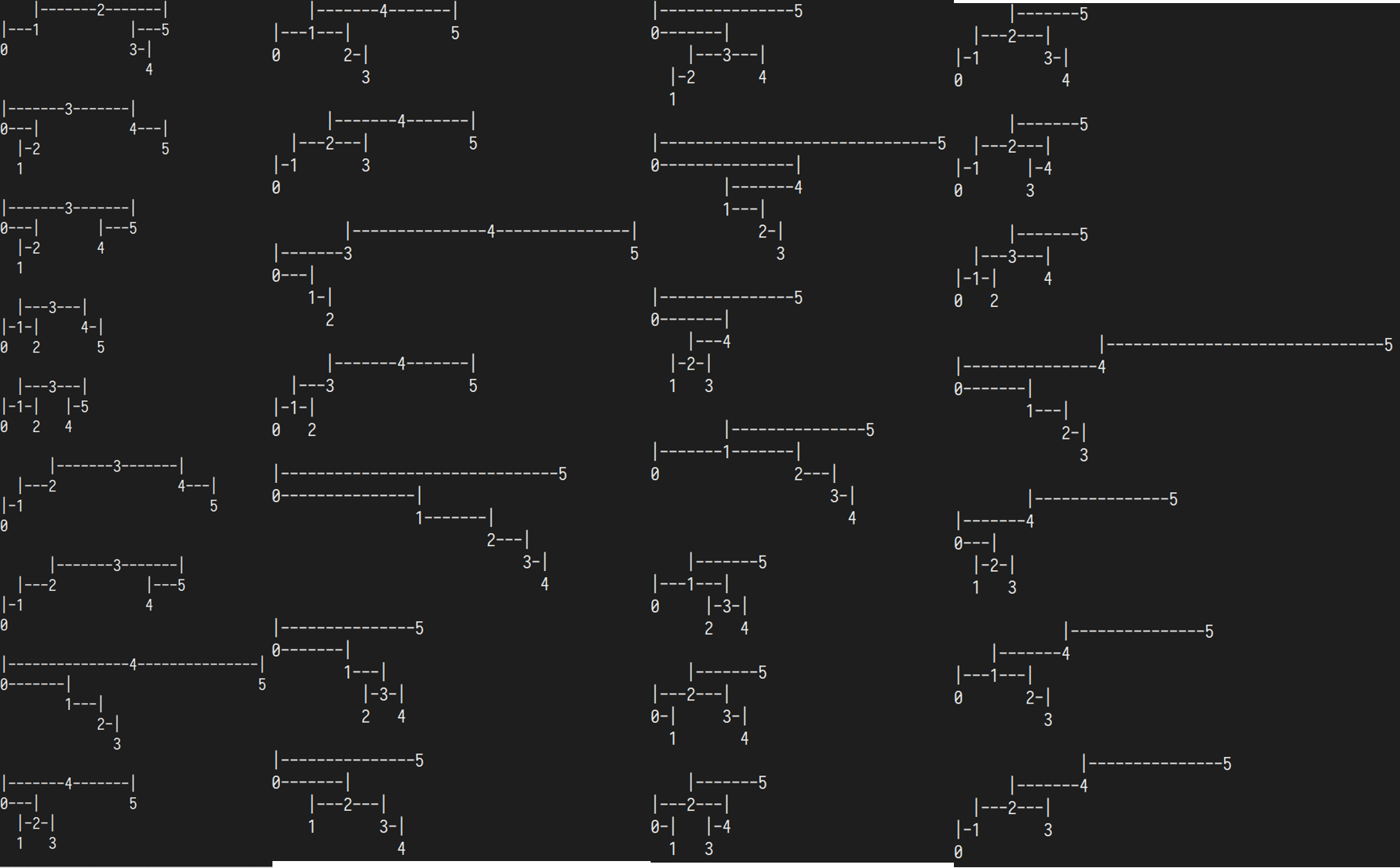
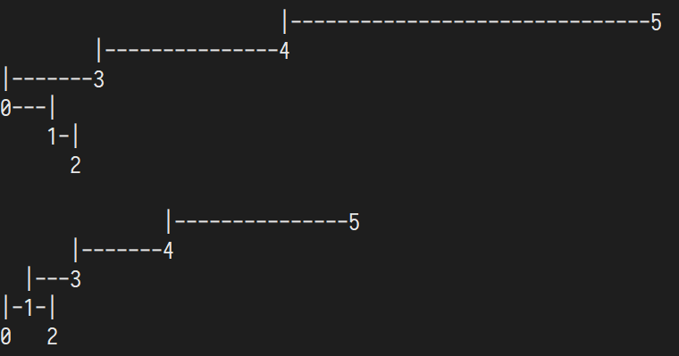
另请参阅

BinarySearchTree 库

3.2.10

解答

官方实现：https://algs4.cs.princeton.edu/32bst/TestBST.java.html

测试结果：

size = 10
min = A
max = X

Testing keys()
---------------------------
A 8
C 4
E 12
H 5
L 11
M 9
P 10
R 3
S 0
X 7

Testing select
---------------------------
0 A
1 C
2 E
3 H
4 L
5 M
6 P
7 R
8 S
9 X

key rank floor ceil
---------------------------
A 0 A A
B 1 A C
C 1 C C
D 2 C E
E 2 E E
F 3 E H
G 3 E H
H 3 H H
I 4 H L
J 4 H L
K 4 H L
L 4 L L
M 5 M M
N 6 M P
O 6 M P
P 6 P P
Q 7 P R
R 7 R R
S 8 S S
T 9 S X
U 9 S X
V 9 S X
W 9 S X
X 9 X X
Y 10 X
Z 10 X
range search
---------------------------
A-Z (11)A C E H L M P R S X
Z-A (0)
X-X (1)X
0-Z (11)A C E H L M P R S X
B-G (3)C E
C-L (4)C E H L

After deleting the smallest 3 keys
---------------------------
H 5
L 11
M 9
P 10
R 3
S 0
X 7

After deleting the remaining keys
---------------------------

After adding back the keys
---------------------------
A 8
C 4
E 12
H 5
L 11
M 9
P 10
R 3
S 0
X 7

3.2.11

解答

树的高度为树中深度最大的点的深度。
因此 N 个结点最多只能构造出高度为 N-1 的树来，并不能构成高度为 N 的树。

如果将题目变为用 N 个结点构造高度为 N-1 的二叉搜索树。
这样的树即为二叉搜索树的最坏情况，除唯一的叶子结点之外，每个结点有且只有一个子树。
于是除根结点外，每个结点都有两种选择，要么在左，要么在右。
因此共有 $2 ^ {n - 1}$ 种形状。

接下来证明，对于某一种确定的最坏情况，在 N 个元素各不相同的情况下，输入顺序是唯一的。
证明：
就 1 2 3 这三个元素而言，构造这样一棵树：

  2
1   3

可以有 2 1 3 和 2 3 1 两种序列，因为在插入 2 之后可以选择的位置有两个
但最坏情况下的二叉搜索树不存在具有两个子结点的结点，因此输入顺序是唯一的。

反证：
也可以这样考虑，假设序列 A 可以构造出一棵最坏情况下的二叉树，插入顺序为 $x_1 \dots x_n$
假设存在与 A 顺序不同的序列 B，它构造出的二叉树与 A 的相同。
由于 A 和 B 的元素相同，因此 A 必然可以通过有限次元素交换得到 B。
根据最坏情况下的二叉搜索树的性质，A 中的元素 $x_n$ 必然满足 $x_1 \dots x_{n - 1}$ 的所有关系。
例如，假设 $x_1 > x_2$，则 $ x_3 $ 也必然满足 $x_1 > x_3$，即后面的元素必然满足前面元素的关系。
于是 A 存在关系序列 $r_1 \dots r_{n - 1}$，只有满足这样序列的输入才能构造出对应的二叉树。
（可以将 $r$ 理解为大于号或者小于号，由于元素各不相同，因此不存在等号）
显然 A 中的任意两个元素交换会导致至少一个 $r$ 倒置，除非进行逆向交换，否则这种倒置不可能消除。
（大于号和小于号是不满足交换律的）
因此 A 和 B 必定相同，得证。

于是每一种最坏情况下的形状都唯一对应一种输入序列，共有 $2 ^ {n - 1}$ 种构造方式。

3.2.12

解答

二叉树的大小=左子树的大小+右子树的大小+1

根据上述表达式可以构造出一个递归的 Size() 方法，并删除结点中的 Size 。
Rank() 和 Select() 仍然可以正常工作，但最坏情况下的耗时可能会达到 $O(n)$ 和 $O(n^2)$。

3.2.13

解答

官方实现：https://algs4.cs.princeton.edu/32bst/NonrecursiveBST.java.html

Get 方法可以很方便的改成非递归形式。

while (cur != null)
{
    var cmp = key.CompareTo(cur.Key);
    if (cmp < 0)
        cur = cur.Left;
    else if (cmp > 0)
        cur = cur.Right;
    else
        return cur.Value;
}

Put 方法结构类似，但需要注意更新路径上各个结点的 Size 属性。

var path = new Stack<Node>();
var cur = x;
while (cur != null)
{
    path.Push(cur); 
    var cmp = key.CompareTo(cur.Key);
    if (cmp < 0)
        cur = cur.Left;
    else if (cmp > 0)
        cur = cur.Right;
    else
    {
        cur.Value = value;
        return x;
    }
}

var parent = path.Peek();
var node = new Node(key, value, 1);
if (parent.Key.CompareTo(key) > 0)
    parent.Left = node;
else
    parent.Right = node;

while (path.Count > 0)
    path.Pop().Size++;

Keys 方法中，可以用新建一个栈来代替递归栈记录路径。

while (x != null || stack.Count > 0)
{
    if (x != null)
    {
        stack.Push(x);
        x = x.Left;
    }
    else
    {
        x = stack.Pop();
        queue.Enqueue(x.Key);
        x = x.Right;
    }
}

另请参阅

BinarySearchTree 库

3.2.14

解答

就 min，max 和 select 而言，它们是尾递归的，可以直接转换成迭代形式。
（简单的说，尾递归就是所有递归操作都出现在 return 语句上，且返回值不需要参与其他运算）

例如 min，递归形式为：

if (x.Left == null)
    return x;
return Min(x.Left);

递归调用获得的值直接返回，不再参与运算，可以直接转换为递推：

while (true)
{
    if (x.Left == null) return x;
    x = x.Left;
}

ceiling 和 floor 会略微复杂一些，具体见代码。

代码

min 和 max 比较简单，用一个 while 循环就可以转换为递推形式，例如 min。

while (x != null)
{
    if (x.Left == null) return x;
    x = x.Left;
}

return x;

floor 和 ceiling 则要稍微复杂一点，需要记录当前找到的最小/最大值，例如 floor。

Node floor = null;
while (x != null)
{
    var cmp = key.CompareTo(x.Key);
    if (cmp == 0)
    {
        return x;
    }

    if (cmp < 0)
    {
        x = x.Left;
    }
    else
    {
        floor = x;
        x = x.Right;
    }
}

return floor;

rank 和它们类似，需要用一个变量记录当前排名。

var rank = 0;
while (x != null)
{
    var cmp = key.CompareTo(x.Key);
    if (cmp < 0)
    {
        x = x.Left;
    }
    else if (cmp > 0)
    {
        rank += 1 + Size(x.Left);
        x = x.Right;
    }
    else
    {
        rank += Size(x.Left);
        return rank;
    }

}

return rank;

select 比较简单，不需要维护变量。

while (x != null)
{
    var t = Size(x.Left);
    if (t > k)
    {
        x = x.Left;
    }
    else if (t < k)
    {
        x = x.Right;
        k = k - t - 1;
    }
    else
    {
        return x;
    }
}

return null;

另请参阅

尾递归-维基百科

BinarySearchTree 库

3.2.15

解答

比较简单，这里比较/取值都算一次访问，因此 keys 的访问序列会出现重复元素。

函数	路径
floor(Q)	E Q
select(5)	E Q
ceiling(Q)	E Q
rank(J)	E Q J
size(D, T)	E Q T E D
keys(D, T)	E D E Q J J M Q T S S T

3.2.16

解答

在高德纳的《计算机程序设计艺术》第一卷里出现了这个公式，编号为 $2.3.4.5(3)$。

书中的证明简单直接：

考虑二叉树中的某个叶子结点 $V$，设根结点到它的路径长度为 $k$，现在将 $V$ 删去。
对于二叉树的内部路径长度 $I$ 和外部路径长度 $E$ ：

由于 $V$ 被删去，$E$ 将会减少 $2(k+1)$，$I$ 将会减少 $k$，但此时 $V$ 变成了一个外部结点，$E$ 又会加上 $k$。
因此最后 $E$ 减少了 $k+2$，$I$ 减少了 $k$，重复 $N$ 次操作之后就可以得到 $E = I + 2N$。

另请参阅

《计算机程序设计艺术：第一卷基本算法》（第三版）P400

3.2.17

解答

像这样，有一些字母是重复的，因此删除后树形状不变：

|-------------------------------E-------------------------------|
A                                               |---------------S---------------|
                                        |-------Q                       |-------Y
                                        I---|                       |---U
                                          |-O                       T
                                          N

|---------------I---------------|
A                       |-------S-------|
                    |---Q           |---Y
                  |-O             |-U
                  N               T

I---------------|
        |-------S-------|
    |---Q           |---Y
  |-O             |-U
  N               T

I---------------|
        |-------T-------|
    |---Q           |---Y
  |-O               U
  N

I---------------|
        |-------T-------|
    |---Q               U
  |-O
  N

I-------|
    |---T---|
  |-O       U
  N

I-------|
    |---T
  |-O
  N

I-------|
    |---T
  |-O
  N

I-------|
    |---T
  |-O
  N

I---|
  |-O
  N

|-O
N

N

3.2.18

解答

和上一题类似，只是删除顺序不同：

|-------------------------------E-------------------------------|
A                                               |---------------S---------------|
                                        |-------Q                       |-------Y
                                        I---|                       |---U
                                          |-O                       T
                                          N

E-------------------------------|
                |---------------S---------------|
        |-------Q                       |-------Y
        I---|                       |---U
          |-O                       T
          N

        |---------------S---------------|
|-------Q                       |-------Y
I---|                       |---U
  |-O                       T
  N

        |---------------S---------------|
|-------Q                       |-------Y
I---|                       |---U
  |-O                       T
  N

      |-------S-------|
  |---Q           |---Y
|-O             |-U
N               T

    |-------S-------|
|---Q           |---Y
O             |-U
              T

|-------S-------|
Q           |---Y
          |-U
          T

S-------|
    |---Y
  |-U
  T

  |---Y
|-U
T

  |---Y
|-U
T

|-Y
U

Y

3.2.19

解答

类似于这样的序列：

|-------------------------------E-------------------------------|
A                                               |---------------S---------------|
                                        |-------Q                       |-------Y
                                        I---|                       |---U
                                          |-O                       T
                                          N

|---------------I---------------|
A                       |-------S-------|
                    |---Q           |---Y
                  |-O             |-U
                  N               T

|---------------N---------------|
A                       |-------S-------|
                    |---Q           |---Y
                    O             |-U
                                  T

|---------------O---------------|
A                       |-------S-------|
                        Q           |---Y
                                  |-U
                                  T

|---------------Q---------------|
A                               S-------|
                                    |---Y
                                  |-U
                                  T

|-------S-------|
A           |---Y
          |-U
          T

|---T---|
A     |-Y
      U

|-U-|
A   Y

|-Y
A

A

3.2.20

解答

勘误：英文版为 keys() 方法（而非 Size() 方法）。

先来观察一下 keys() 方法的实现：

public IEnumerable<TKey> Keys(TKey lo, TKey hi)
{
    var queue = new Queue<TKey>();
    Keys(root, queue, lo, hi);
    return queue;
}

private void Keys(Node x, Queue<TKey> queue, TKey lo, TKey hi)
{
    var cmplo = lo.CompareTo(x.Key);
    var cmphi = hi.CompareTo(x.Key);
    if (cmplo < 0)
        Keys(x.Left, queue, lo, hi);
    if (cmplo <= 0 && cmphi >= 0)
        queue.Enqueue(x.Key);
    if (cmphi > 0)
        Keys(x.Right, queue, lo, hi);
}

简单地说，就是从根结点同时向两侧查找，同时把中间的键加入到队列中（树高的倍数+范围内键的数量）。

于是 Keys() 的耗时可以分成两部分：
寻找小于 lo 的最大键值和大于 hi 的最小键值在最坏情况下需要的访问结点数——即树高。
（例如当 lo 小于树中的最小键或者 hi 大于树中最大键时）
以及访问 lo 和 hi 之间所有结点。

3.2.21

解答

要注意保持每个键的出现概率相等，可以先随机一个排名，然后从树中将对应排名的键取出来。

private static readonly Random Random = new Random();

public TKey RandomKey()
{
    var rank = Random.Next(1, Size() + 1);
    return GetKeyWithRank(root, rank);
}

private TKey GetKeyWithRank(Node x, int rank)
{
    var left = (x.Left == null ? 0 : x.Left.Size) + 1;
    if (left > rank)
    {
        return GetKeyWithRank(x.Left, rank);
    }
    else if (left == rank)
    {
        return x.Key;
    }
    else
    {
        return GetKeyWithRank(x.Right, rank - left);
    }
}

可以观察到每个键的出现概率都是差不多的。

另请参阅

BinarySearchTree 库

3.2.22

解答

这里的前驱和后继指的是二叉树中序遍历序列里结点的前驱和后继。

由于二叉搜索树的性质，它的中序遍历序列是递增有序的。
因此一个结点如果有左子树，要么前驱就是左子树中最大的结点（最右侧）；
同理结点如果有右子树，要么后继就是右子树中最小的结点（最左侧）。

于是结点的前驱不会有右子节点，后继不会有左子节点，得证。

3.2.23

解答

不满足，反例如下：

    |-------10
|---5---|
3     |-8-|
      6   9

Delete 5 then delete 3
|-------10
6---|
    8-|
      9

Delete 3 then delete 5
  |---10
|-8-|
6   9

这里先删除 3 会使 5 的左子树为空，导致删除 5 的时候采取的策略被改变（尽管 5 的右子树没有任何变化）。

另请参阅

Deletion procedure for a Binary Search Tree-Stackoverflow

3.2.24

解答

根据命题 D （英文版 P404，中文版 P255），一次插入所需的比较次数平均为 $1.39\lg N$。
(我们这里要求和，因此可以直接使用平均值进行计算）
于是构造一棵二叉查找树所需的比较次数为：

\[1.39C= 1.39\sum_{i=0}^N \lg i=1.39 \times(\lg 1 + \lg2+\cdots+\lg N) \]

根据对数恒等式，有：

\[C=\lg 1 + \lg2+\cdots+\lg N=\lg(1\times2\times3\times\cdots\times N)=\lg(N!) \]

于是有 $1.39C=1.39\lg(N!) > \lg(N!)$ ，得证。

3.2.25

解答

官方实现：https://algs4.cs.princeton.edu/32bst/PerfectBalance.java.html

先排序，然后视其为中序序列，每次取中间的键作为根结点，左半数组是左子树，右半数组是右子树，递归构造。

private Node BuildTree(KeyValuePair<TKey, TValue>[] init, int lo, int hi)// init is sorted
{
    if (lo > hi)
    {
        return null;
    }

    var mid = (hi - lo) / 2 + lo;
    var current = new Node(init[mid].Key, init[mid].Value, 1);
    current.Left = BuildTree(init, lo, mid - 1);
    current.Right = BuildTree(init, mid + 1, hi);
    if (current.Left != null)
    {
        current.Size += current.Left.Size;
    }

    if (current.Right != null)
    {
        current.Size += current.Right.Size;
    }
    return current;
}

另请参阅

BinarySearchTree 库

3.2.26

解答

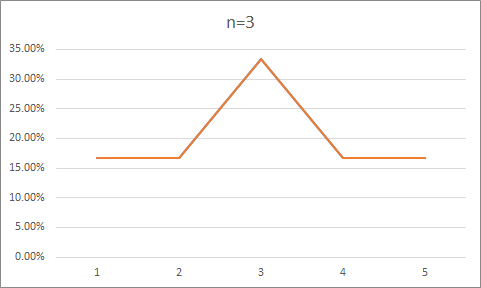
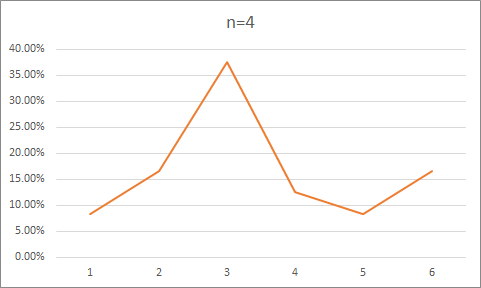
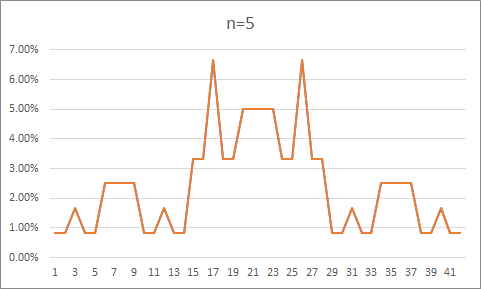
在 3.2.9 的代码基础上进行修改，统计每种形状的出现次数，以此获得准确的概率。

概率如下，基本呈现正态分布。

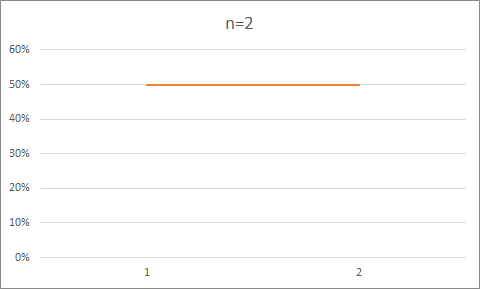
原始数据：

n=2
50%
50%

n=3
16.666666%
16.666666%
33.333332%
16.666666%
16.666666%

n=4
8.333333%
16.666666%
37.5%
12.5%
8.333333%
16.666666%

n=5
0.8333333%
0.8333333%
1.6666666%
0.8333333%
0.8333333%
2.5%
2.5%
2.5%
2.5%
0.8333333%
0.8333333%
1.6666666%
0.8333333%
0.8333333%
3.3333333%
3.3333333%
6.6666665%
3.3333333%
3.3333333%
5%
5%
5%
5%
3.3333333%
3.3333333%
6.6666665%
3.3333333%
3.3333333%
0.8333333%
0.8333333%
1.6666666%
0.8333333%
0.8333333%
2.5%
2.5%
2.5%
2.5%
0.8333333%
0.8333333%
1.6666666%
0.8333333%
0.8333333%

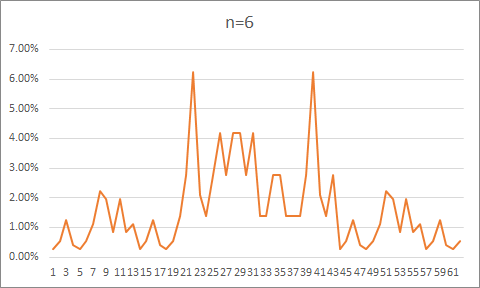
n=6
0.2777778%
0.5555556%
1.25%
0.41666666%
0.2777778%
0.5555556%
1.1111112%
2.2222223%
1.9444444%
0.8333333%
1.9444444%
0.8333333%
1.1111112%
0.2777778%
0.5555556%
1.25%
0.41666666%
0.2777778%
0.5555556%
1.3888888%
2.7777777%
6.25%
2.0833333%
1.3888888%
2.7777777%
4.1666665%
2.7777777%
4.1666665%
4.1666665%
2.7777777%
4.1666665%
1.3888888%
1.3888888%
2.7777777%
2.7777777%
1.3888888%
1.3888888%
1.3888888%
2.7777777%
6.25%
2.0833333%
1.3888888%
2.7777777%
0.2777778%
0.5555556%
1.25%
0.41666666%
0.2777778%
0.5555556%
1.1111112%
2.2222223%
1.9444444%
0.8333333%
1.9444444%
0.8333333%
1.1111112%
0.2777778%
0.5555556%
1.25%
0.41666666%
0.2777778%
0.5555556%

3.2.27

解答

二叉查找树的内存开销=对象开销+根结点引用+N个结点
=对象开销+根结点引用+N×(对象开销+父类型引用+左/右子树引用+键/值引用+结点数)
=16+8+N×(16+8+16+16+4+4)=24+64N 字节

BinarySearchST：对象开销+键/值数组引用+键/值数组+计数器（一个 int）。
=16+16+(16+4+4+8N)×2+4+4=88+16N 字节。

SequentialSearchST：对象开销+头结点引用+N个结点+计数器
=对象开销+头结点引用+N×(对象开销+父类型引用+next引用+键/值引用)+计数器
=16+8+N×(16+8+8+16)+4+4=32+48N 字节

示意图如下：

其中，对象开销 16 字节，其他均为引用，各占 8 字节。

《双城记》中不重复的单词有 26436 个（不包括最后的版权声明），全部是原文的子字符串，每个占 40 字节。
一个 Integer 占 24 字节，于是估计的内存消耗为：24+(64+40+24)×26436=3383832 字节。

3.2.28

解答

修改一下 Put 和 Get 方法，在实际操作之前先检查缓存是否符合要求，然后在操作之后更新缓存。

代码

private Node _cache;

public override TValue Get(TKey key)
{
    if (_cache != null && _cache.Key.CompareTo(key) == 0)
    {
        return _cache.Value;
    }

    return Get(root, key).Value;
}

protected override Node Get(Node x, TKey key)
{
    if (key == null)
    {
        throw new ArgumentNullException("calls get() with a null key");
    }

    if (x == null)
    {
        return null;
    }
    var cmp = key.CompareTo(x.Key);
    if (cmp < 0)
    {
        return Get(x.Left, key);
    }
    else if (cmp > 0)
    {
        return Get(x.Right, key);
    }
    else
    {
        _cache = x;
        return x;
    }
}

public override void Put(TKey key, TValue value)
{
    if (key == null)
    {
        throw new ArgumentNullException("calls Put() with a null key");
    }

    if (value == null)
    {
        Delete(key);
        return;
    }

    if (_cache != null && _cache.Key.CompareTo(key) == 0)
    {
        _cache.Value = value;
        return;
    }
    root = Put(root, key, value);
}

protected override Node Put(Node x, TKey key, TValue value)
{
    if (x == null)
    {
        _cache = new Node(key, value, 1);
        return _cache;
    }
    var cmp = key.CompareTo(x.Key);
    if (cmp < 0)
        x.Left = Put(x.Left, key, value);
    else if (cmp > 0)
        x.Right = Put(x.Right, key, value);
    else
        x.Value = value;
    x.Size = 1 + Size(x.Left) + Size(x.Right);
    return x;
}

另请参阅

BinarySearchTree 库

3.2.29

解答

本题在原书后续印刷中已修改，这里仍采用中文版的题目。

部分解答：https://algs4.cs.princeton.edu/32bst/BST.java.html（isSizeConsistent()）

如果根结点记录的结点数=左子树的结点数+右子树的结点数+1，就符合要求。
按照这个题意编制递归方法即可。

先写边界，当输入为 null 时，显然符合要求。
然后计算左子树的 Size 和右子树的 Size 加起来是否等于根结点的 Size + 1，
以及左子树和右子树是否符合同样的条件。

代码

protected static bool IsBinaryTree(Node x)
{
    if (x == null)
    {
        return true;    // 空树显然符合二叉树条件。
    }

    var size = 1;       // 包括当前结点本身。
    if (x.Left != null)
    {
        size += x.Left.Size;
    }

    if (x.Right != null)
    {
        size += x.Right.Size;
    }

    return  IsBinaryTree(x.Left) && 
            IsBinaryTree(x.Right) && 
            x.Size == size;
}

另请参阅

BinarySearchTree 库

3.2.30

解答

本题在原书后续印刷中已修改，这里仍然采用中文版的题目。

与上一题非常类似，条件有：
根结点必须在 min 和 max 范围内，
且左右子树要么不存在，要么小于/大于根结点的键，
左右子树同样满足上述条件。

代码

protected static bool IsOrdered(Node x, TKey min, TKey max)
{
    if (x == null)
    {
        return true;        // 空树显然是满足要求的。
    }

    return IsOrdered(x.Left, min, max) &&
           IsOrdered(x.Right, min, max) &&                        // 左右子树都满足要求。
           x.Key.CompareTo(max) <= 0 &&
           x.Key.CompareTo(min) >= 0 &&                           // 当前结点位于范围内。
           (x.Left == null || x.Left.Key.CompareTo(x.Key) < 0) &&
           (x.Right == null || x.Right.Key.CompareTo(x.Key) > 0); // 当前结点与子结点满足大小关系。
}

另请参阅

BinarySearchTree 库

3.2.31

解答

本题在原书后续印刷中已删除，这里仍然采用中文版的题目。

注意这个题并没有递归的要求，直接广度优先搜索即可，随时记录和检查已找到的键。

代码

protected static bool HasNoDuplicates(Node x)
{
    var keys = new List<TKey>();    // 也可以用 HashSet 之类的数据结构提高效率。
    var queue = new Queue<Node>();
    queue.Enqueue(x);
    while (queue.Count > 0)
    {
        var node = queue.Dequeue();
        if (node == null)
        {
            continue;
        }

        if (keys.Contains(node.Key))
        {
            return false;
        }
        keys.Add(node.Key);
        queue.Enqueue(node.Left);
        queue.Enqueue(node.Right);
    }

    return true;
}

另请参阅

BinarySearchTree 库

3.2.32

解答

本题在原书后续印刷中已修改，这里仍然采用中文版的题目。

官网解答见：https://algs4.cs.princeton.edu/32bst/BST.java.html （isBST()）

书中已经给出了答案，当然在 Java 和 C# 里，&& 总是从左向右计算的，而且遇到 false 会直接返回结果。

如果数据结构中存在环，IsOrdered 有可能会陷入无限递归的情况，因此调用顺序比较重要。

代码

public static bool IsBST(BST<TKey, TValue> bst)
{
    return IsBinaryTree(bst) &&
           IsOrdered(bst) &&
           HasNoDuplicates(bst);
}

另请参阅

Boolean logical operators (C# reference)

Equality, Relational, and Conditional Operators

BinarySearchTree 库

3.2.33

解答

官网解答见：https://algs4.cs.princeton.edu/32bst/BST.java.html （isRankConsistent()）

按照题目要求实现即可，分为两步进行测试。

代码

public static bool IsRankConsistent(BST<TKey, TValue> bst)
{
    for (var i = 0; i < bst.Size(); i++)
    {
        if (i != bst.Rank(bst.Select(i)))
        {
            return false;
        }
    }

    foreach (var key in bst.Keys())
    {
        if (key.CompareTo(bst.Select(bst.Rank(key))) != 0)
        {
            return false;
        }
    }

    return true;
}

另请参阅

BinarySearchTree 库

3.2.34

解答

其实就是将所有的结点按照中序序列排成了一个双向链表，对树进行修改时要同时更新这个双向链表。

当插入新结点时，插到左侧的结点会变为父结点的新前驱，同理右侧会变为新后继。
注意要更新父结点原来的前驱和后继结点（如果有）。

删除结点时较为简单，只要更新需要删除结点的前驱和后继结点即可。

原本操作 left 和 right 的代码不需要更改，只需要加上对 prev 和 next 做操作的代码即可。

Prev 方法实现如下（Next 类似），修改了内部的 Get 方法使之返回 Node 而非 TValue。

public TKey Prev(TKey key)
{
    var node = Get(root, key);
    if (node == null || node.Prev == null)
        return null;
    return node.Prev.Key;
}

代码

处理结点关系的几个方法。

private void DeleteNode(Node x)
{
    if (x.Prev != null)
        x.Prev.Next = x.Next;
    if (x.Next != null)
        x.Next.Prev = x.Prev;
}
private void InsertRight(Node parent, Node newNode)
{
    parent.Right = newNode;
    InsertBetween(parent, newNode, parent.Next);
}
private void InsertLeft(Node parent, Node newNode)
{
    parent.Left = newNode;
    InsertBetween(parent.Prev, newNode, parent);
}
private void InsertBetween(Node prev, Node newNode, Node next)
{
    newNode.Prev = prev;
    newNode.Next = next;

    if (prev != null)
        prev.Next = newNode;
    if (next != null)
        next.Prev = newNode;
}

Put 方法

protected virtual Node Put(Node x, TKey key, TValue value)
{
    if (x == null)
    {
        return new Node(key, value, 1); // 树是空的。
    }
    var cmp = key.CompareTo(x.Key);
    if (cmp < 0)
    {
        if (x.Left == null)
        {
            var newNode = new Node(key, value, 1);
            InsertLeft(x, newNode);
        }
        else
        {
            x.Left = Put(x.Left, key, value);
        }
    }
    else if (cmp > 0)
    {
        if (x.Right == null)
        {
            var newNode = new Node(key, value, 1);
            InsertRight(x, newNode);
        }
        else
        {
            x.Right = Put(x.Right, key, value);
        }
    }
    else
    {
        x.Value = value;
    }
    x.Size = 1 + Size(x.Left) + Size(x.Right);
    return x;
}

Delete 方法

protected virtual Node Delete(Node x, TKey key)
{
    if (x == null)
        return null;

    var cmp = key.CompareTo(x.Key);
    if (cmp < 0)
        x.Left = Delete(x.Left, key);
    else if (cmp > 0)
        x.Right = Delete(x.Right, key);
    else
    {
        DeleteNode(x);          // 在中序链表中删除结点。
        if (x.Right == null)
            return x.Left;
        if (x.Left == null)
            return x.Right;
        var t = x;
        x = Min(t.Right);
        x.Right = DeleteMin(t.Right);
        x.Left = t.Left;
    }
    x.Size = Size(x.Left) + Size(x.Right) + 1;
    return x;
}

DeleteMin 方法，DeleteMax 类似。

protected virtual Node DeleteMin(Node x)
{
    if (x.Left == null)
    {
        DeleteNode(x);
        return x.Right;
    }
    x.Left = DeleteMin(x.Left);
    x.Size = Size(x.Left) + Size(x.Right) + 1;
    return x;
}

另请参阅

BinarySearchTree 库

3.2.35

解答

根据书中已经给出的归纳关系式（中文版P255/英文版P403）：

\[C_N=N-1+(C_0+C_{N-1})/N+(C_1+C_{N-2})/N+\cdots+(C_{N-1}+C_0)/N \]

整理得：

\[C_N=N-1+(C_0+C_1+\cdots+C_{N-1})/N+(C_{N-1}+\cdots+C_1+C_0)/N \]

这和快速排序的式子基本一致，只是 $ N+1 $ 变成了 $ N-1 $。

遵循相同的推导过程，我们可以获得类似的结果，两边同乘以 $ N $：

\[NC_N=N(N-1)+2(C_0+C_1+\cdots+C_{N-1}) \]

用 $ N+1 $ 时的等式减去该式得：

\[(N+1)C_{N+1}-NC_N=2N+2C_N \\ (N+1)C_{N+1}=2N+(N+2)C_N \\ \frac{C_{N+1}}{N+2}=\frac{2N}{(N+1)(N+2)} + \frac{C_N}{N+1} \]

令 $ T_N = \frac{C_N}{N+1} $，得到：

\[T_{N+1}=\frac{2N}{(N+1)(N+2)} + T_N \\ T_{N+1}-T_{N} = \frac{2N}{(N+1)(N+2)} \]

归纳得：

\[\begin{aligned} T_N &= 2 \sum_{i=2}^{N} \frac{i-1}{i(i+1)} \\ C_N&=2(N+1)\sum_{i=2}^{N} \frac{i-1}{i(i+1)} \\ C_N&=2(N+1)\sum_{i=2}^{N}(i-1) (\frac{1}{i}-\frac{1}{i+1}) \\ C_N&=-2(N-1)+ 2(N+1)\sum_{i=2}^{N}\frac{1}{i}\\ C_N&=-2(N-1)+ 2(N+1)(-1+\sum_{i=1}^{N}\frac{1}{i})\\ C_N&=-4N+2(N+1)(\ln N+\gamma) \end{aligned} \]

于是平均成本为：$1+C_N/N \sim 2\ln N+2\gamma-3$ 。

3.2.36

解答

用一个栈来模拟递归即可，将路径上的结点记录到栈里。
注意 Queue<TKey> 不算额外空间，因为它在keys执行完毕之后不会被回收。

代码

private void Keys(Node x, Queue<TKey> queue, TKey lo, TKey hi)
{
    var stack = new Stack<Node>();

    while (x != null || stack.Count > 0)
    {
        if (x != null)
        {
            var cmpLo = lo.CompareTo(x.Key);
            var cmpHi = hi.CompareTo(x.Key);
            if (cmpHi >= 0)
                stack.Push(x);
            if (cmpLo < 0)
                x = x.Left;
            else
                x = null;
        }
        else
        {
            x = stack.Pop();
            var cmpLo = lo.CompareTo(x.Key);
            var cmpHi = hi.CompareTo(x.Key);
            if (cmpLo <= 0 && cmpHi >= 0)
                queue.Enqueue(x.Key);
            x = x.Right;
        }
    }
}

另请参阅

BinarySearchTree 库

3.2.37

解答

二叉树层序遍历，出队一个结点，打印它，将结点的左右子树入队，循环即可。

代码

private void PrintLevel(Node x)
{
    var queue = new Queue<Node>();
    queue.Enqueue(x);
    while (queue.Count > 0)
    {
        var node = queue.Dequeue();
        if (node.Left != null)
            queue.Enqueue(node.Left);
        if (node.Right != null)
            queue.Enqueue(node.Right);
        Console.Write(node.Key + ", ");
    }
}

另请参阅

BinarySearchTree 库

3.2.38

解答

通过层序遍历计算结点的坐标，然后绘制即可。
先算出最大深度，确定每一层的高度 Y，
再将每一层的宽度分成 $2^n-1$ 份，从左到右依次对结点赋值。

效果如下：

代码

计算坐标的函数。

public void DrawTree(Graphics pen, RectangleF panel)
{
    var depth = Depth(root); // 确定最大深度。
    var layerHeight = panel.Height / depth;
    var nowLayer = new Queue<Node>();
    var nextLayer = new Queue<Node>();
    nextLayer.Enqueue(root);

    for (var layer = 0; layer != depth; layer++)
    {
        var unitSizeX = (float)(panel.Width / Math.Pow(2, layer));
        var temp = nowLayer;
        nowLayer = nextLayer;
        nextLayer = temp;

        var cursorX = 0.0f;
        var cursorY = layer * layerHeight;
        while (nowLayer.Count != 0)
        {
            var node = nowLayer.Dequeue();

            if (node != null)
            {
                nextLayer.Enqueue(node.Left);
                nextLayer.Enqueue(node.Right);
            }
            else
            {
                nextLayer.Enqueue(null);
                nextLayer.Enqueue(null);
            }


            if (node != null)
            {
                node.X = cursorX + unitSizeX / 2.0f;
                node.Y = cursorY;
            }
            
            cursorX += unitSizeX;
        }
    }
}

3.2.39

解答

测试结果：

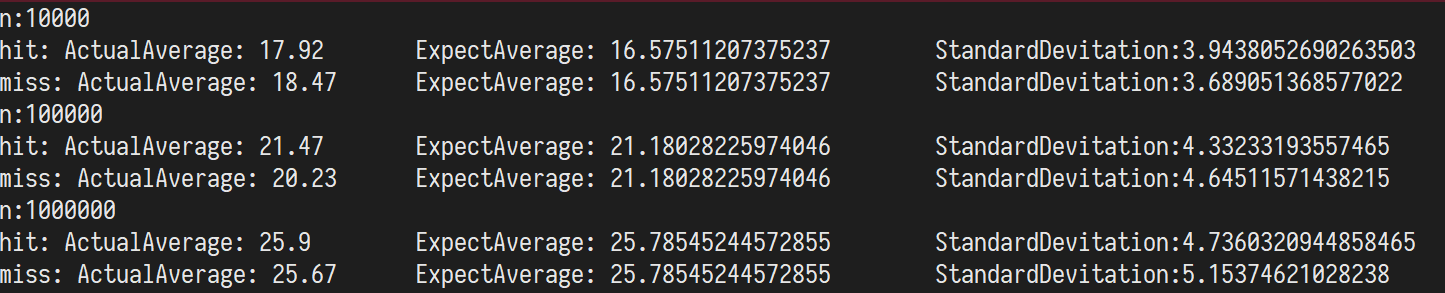
可以看到和公式给出的结果十分一致。

测试时先生成 0~2n 顺序序列，奇数插入二叉树中，偶数用于测试查找失败的情况。

代码

static void Main(string[] args)
{
    var n = 10000;
    var trial = 100;
    for (var i = 0; i < 3; i++)
    {
        var odds = new int[n];
        var evens = new int[n];
        var bst = new BSTAnalysis<int, int>();
        for (var j = 100; j < n; j++)
        {
            evens[j] = j;
            odds[j] = j + 1;
        }
        Shuffle(odds);
        foreach (var item in odds)
        {
            bst.Put(item, item);
        }

        Console.WriteLine("n:" + n);
        // hit
        Shuffle(odds);
        Test(bst, odds, trial, "hit");

        // miss
        Shuffle(evens);
        Test(bst, evens, trial, "miss");

        n *= 10;
    }
}

static void Test(BSTAnalysis<int, int> bst, int[] testCases, int trials, string label)
{
    var testRecords = new long[trials];
    for (var j = 0; j < trials; j++)
    {
        bst.CompareTimes = 0;             // reset
        bst.Get(testCases[j]);            // test
        testRecords[j] = bst.CompareTimes; // record
    }

    var testAverage = 0d;        // 'd' for double
    foreach (var record in testRecords)
    {
        testAverage += record;
    }

    testAverage /= testRecords.Length;

    var testStandardDeviation = 0d;
    foreach (var record in testRecords)
    {
        testStandardDeviation += (record - testAverage) * (record - testAverage);
    }

    testStandardDeviation /= testRecords.Length;
    testStandardDeviation = Math.Sqrt(testStandardDeviation);
    // 2lnN + 2γ - 3
    var expect = 2 * Math.Log(testCases.Length) + 2 * 0.5772156649 - 3;
    Console.WriteLine(label + ": ActualAverage: " + testAverage + "\tExpectAverage: " + expect + "\tStandardDevitation:" + testStandardDeviation);
}

static void Shuffle<T>(T[] a)
{
    var random = new Random();
    for (var i = 0; i < a.Length; i++)
    {
        var r = i + random.Next(a.Length - i);
        var temp = a[i];
        a[i] = a[r];
        a[r] = temp;
    }
}

另请参阅

BinarySearchTree 库

3.2.40

解答

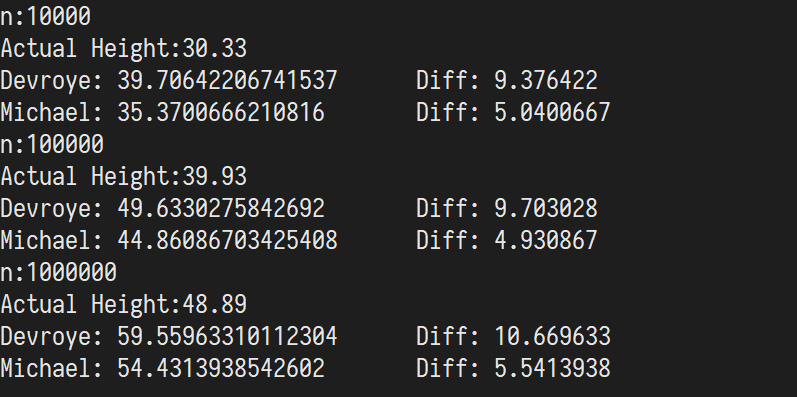
书中的结论是 1986 年 L. Devroye 给出的，原式为 $H_n \rightarrow c\log(n)$。

其中 $c$ 是方程 $c\log \frac{2e}{c}=1$ 的最大解，约为 $4.31107$。

2002 年 Michael Drmota 给出了一个跟精确的公式：$\mathrm{E}(H_n)=c\log n-\frac{3c}{2(c-1)}\log \log n + O(1)$。

测试结果如下，误差基本稳定在一个常数。

代码

static void Main(string[] args)
{
    var n = 10000;
    var trials = 100;

    for (var i = 0; i < 3; i++)
    {
        var items = new int[n];
        
        for (var j = 0; j < n; j++)
        {
            items[j] = j;
        }

        var aveHeight = 0d;
        for (var j = 0; j < trials; j++)
        {
            var bst = new BST<int, int>();
            Shuffle(items);
            foreach (var item in items)
            {
                bst.Put(item, item);
            }

            aveHeight += bst.Height();
        }

        aveHeight /= trials;
        var c = 4.31107d;
        var expectHeightLuc = c * Math.Log(n);
        var expectHeightMichael = c * Math.Log(n) - (3 * c / (2 * (c - 1))) * Math.Log(Math.Log(n));
        Console.WriteLine("n:" + n);
        Console.WriteLine("Actual Height:" + aveHeight);
        Console.WriteLine("Devroye: " + expectHeightLuc + "\tDiff: " + (float)(expectHeightLuc - aveHeight));
        Console.WriteLine("Michael: " + expectHeightMichael + "\tDiff: " + (float)(expectHeightMichael - aveHeight));

        n *= 10;
    }
}

static void Shuffle<T>(T[] a)
{
    var random = new Random();
    for (var i = 0; i < a.Length; i++)
    {
        var r = i + random.Next(a.Length - i);
        var temp = a[i];
        a[i] = a[r];
        a[r] = temp;
    }
}

另请参阅

A note on the height of binary search tree

Note The Variance of the height of binary search trees

BinarySearchTree 库

3.2.41

解答

大体上和标准 BST 实现差不多，做如下变换即可：

x.Key => _nodes[x].Key;
x.Value => _nodes[x].Value;
x.Left => _left[x];
x.Right => _right[x];

由于使用了数组，在正常「删除」二叉树结点之后，还需要手工「垃圾回收」，如下图所示：

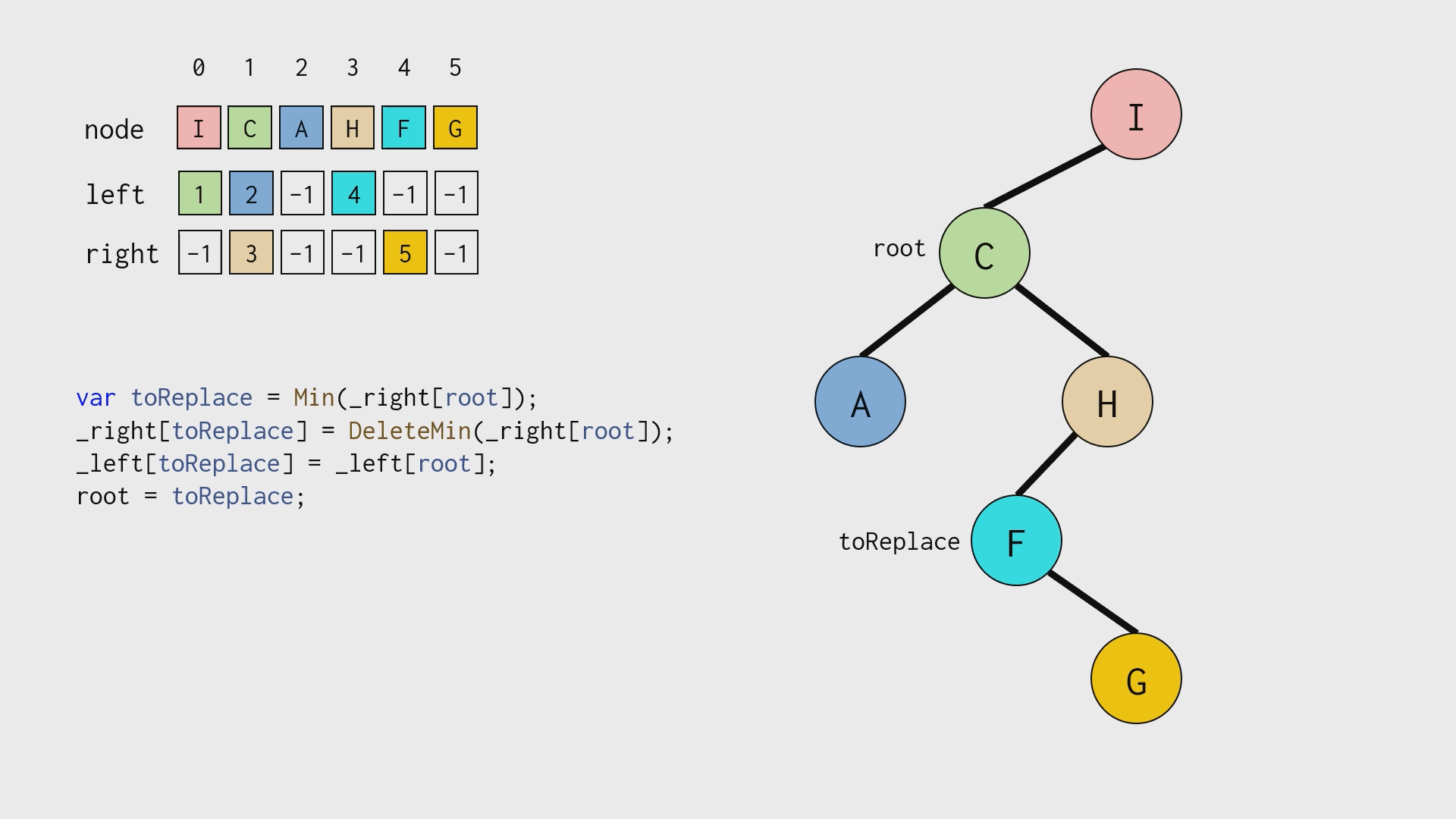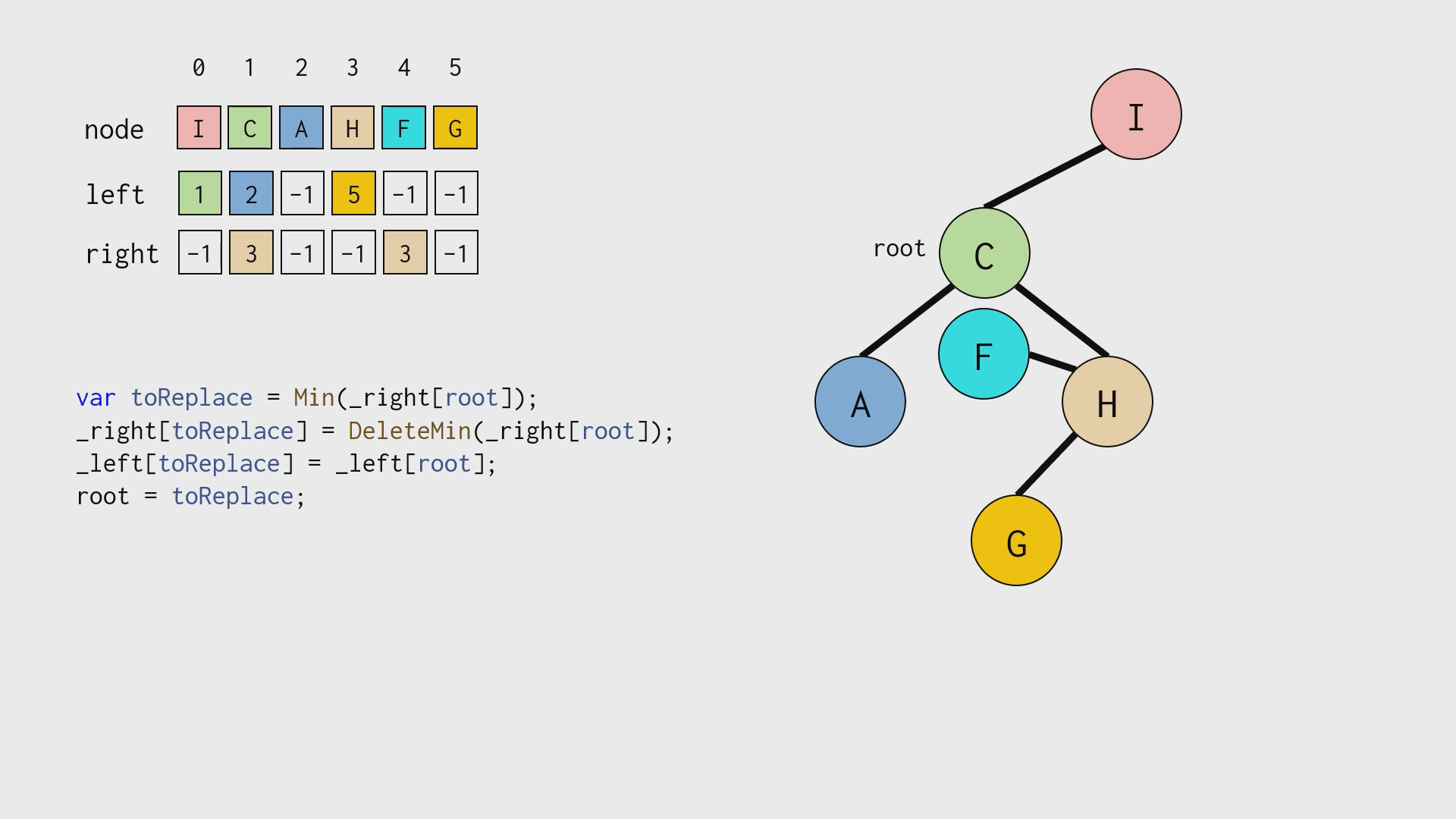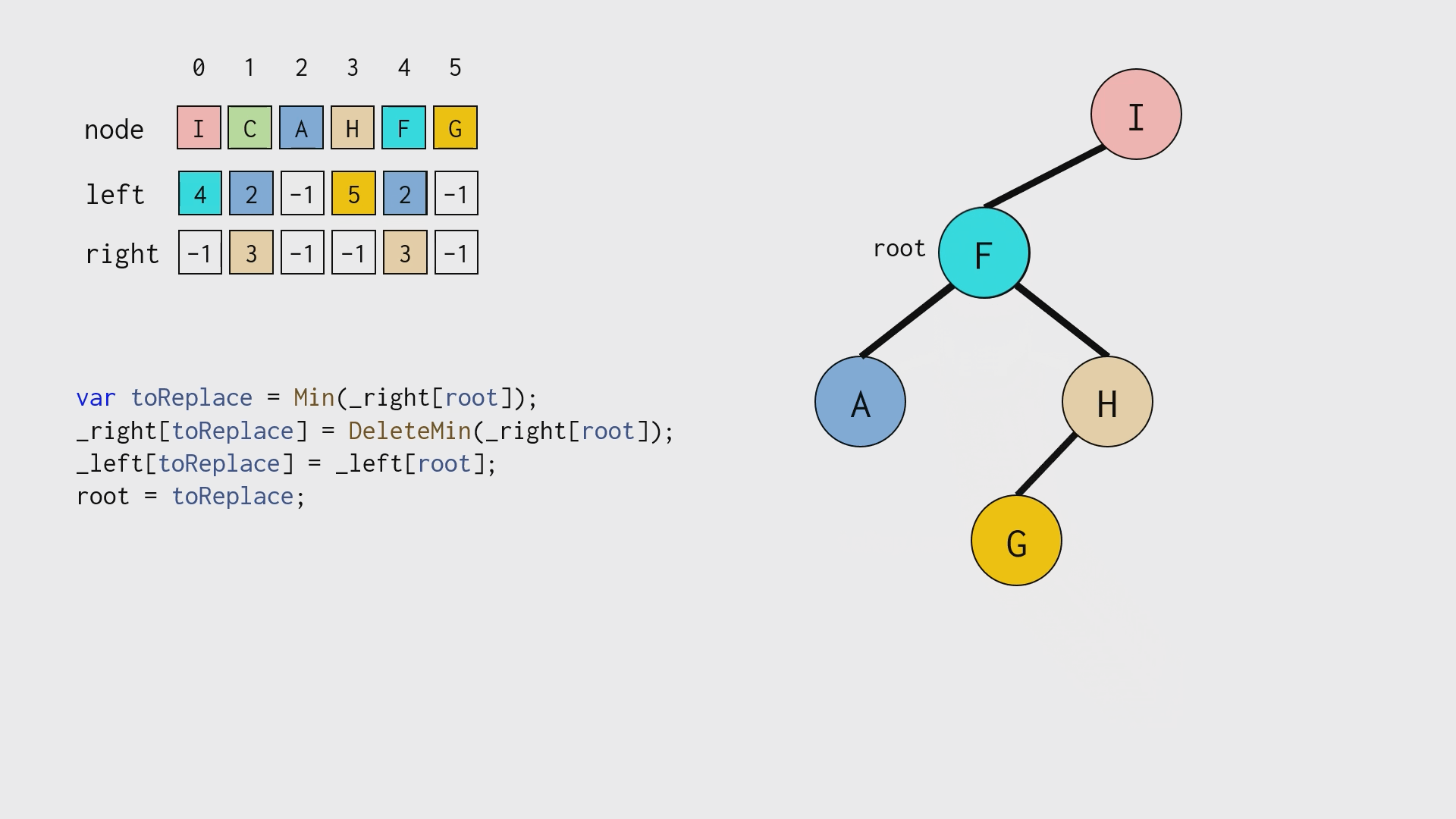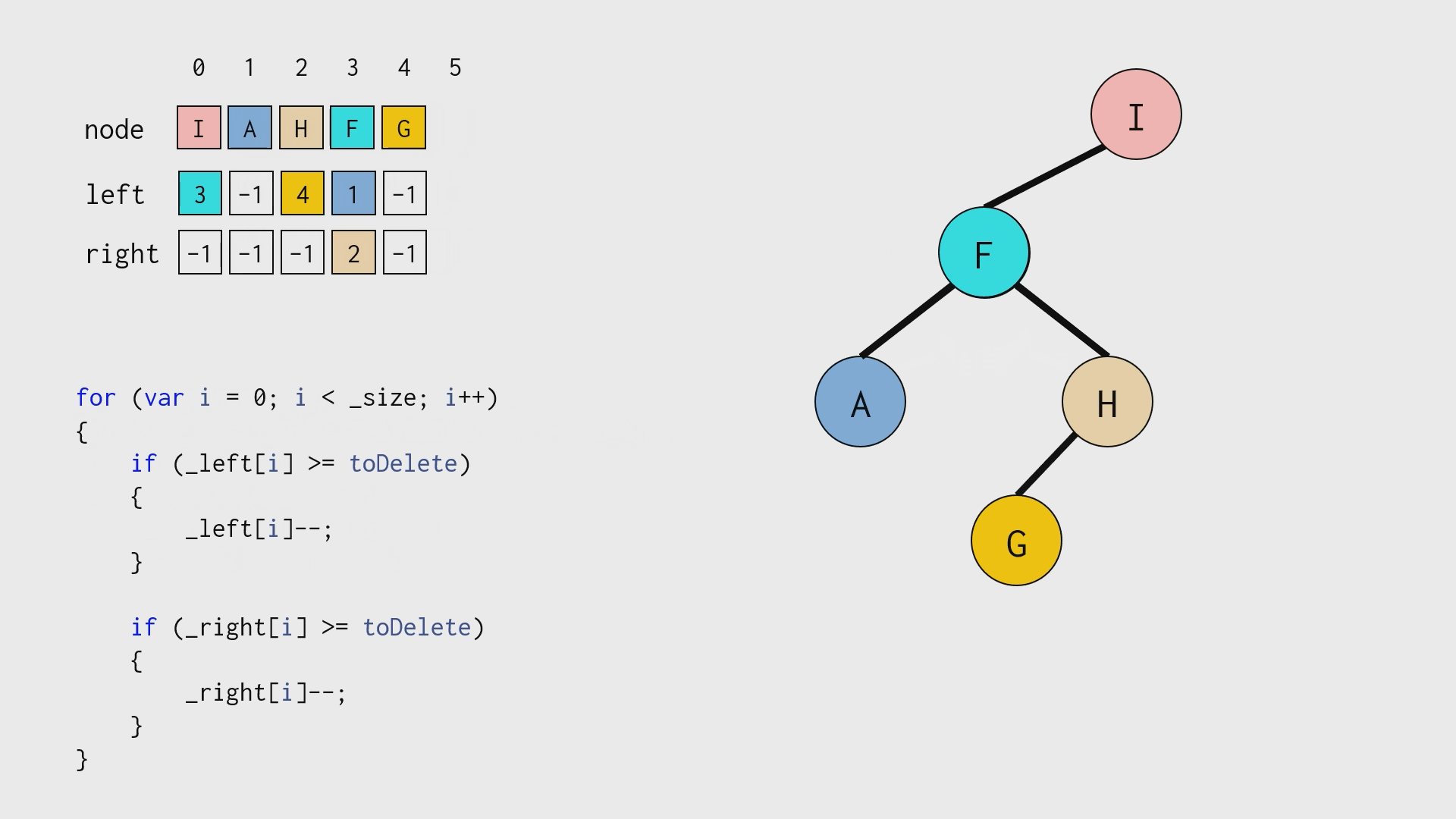
性能比较：

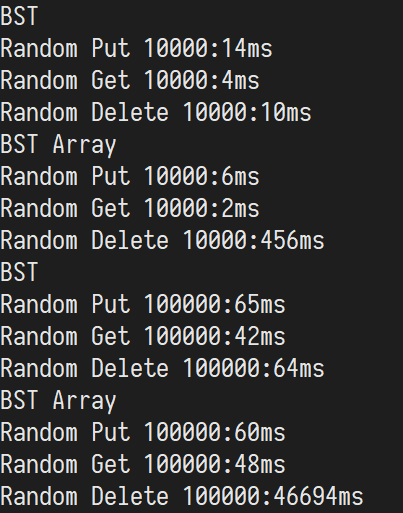
可见数组实现在删除节点时有巨大的性能差距。

代码

private readonly Node[] _nodes;
private readonly int[] _left;
private readonly int[] _right;
private int _size;
private int _root;

/// <summary>
/// 二叉搜索树的结点。
/// </summary>
private class Node
{
    public TKey Key { get; set; }
    public TValue Value { get; set; }
}

/// <summary>
/// 建立一个以数组为基础的二叉搜索树。
/// </summary>
/// <param name="maxSize">二叉搜索树中的结点数。</param>
public BSTArray(int maxSize)
{
    _nodes = new Node[maxSize];
    _left = new int[maxSize];
    _right = new int[maxSize];
    for (var i = 0; i < maxSize; i++)
    {
        _left[i] = -1;
        _right[i] = -1;
    }
    _size = 0;
    _root = 0;
}

/// <summary>
/// 向符号表插入键值对。
/// </summary>
/// <param name="key">键。</param>
/// <param name="value">值。</param>
public void Put(TKey key, TValue value)
{
    if (_size == _nodes.Length)
    {
        throw new InvalidOperationException("BST is full");
    }

    if (IsEmpty())
    {
        _nodes[_size] = new Node{Key = key, Value = value};
        _size++;
        return;
    }

    Put(key, value, null, _root);
}

/// <summary>
/// 向二叉树插入键值对。
/// </summary>
/// <param name="key">键。</param>
/// <param name="value">值。</param>
/// <param name="treeSide">子树数组。</param>
/// <param name="parent">父结点下标。</param>
private void Put(TKey key, TValue value, int[] treeSide, int parent)
{
    int now;
    if (treeSide == null)               // init
    {
        now = parent;
    }
    else if (treeSide[parent] == -1)    // finish
    {
        _nodes[_size] = new Node { Key = key, Value = value };
        treeSide[parent] = _size;
        _size++;
        return;
    }
    else
    {
        now = treeSide[parent];
    }

    var cmp = _nodes[now].Key.CompareTo(key);
    if (cmp > 0)
    {
        Put(key, value, _left, now);
    }
    else if (cmp < 0)
    {
        Put(key, value, _right, now);
    }
    else
    {
        _nodes[now].Value = value;
    }
}

/// <summary>
/// 获取键 <paramref name="key"/> 对应的值，不存在则返回 <c>default(Value)</c>。
/// </summary>
/// <param name="key">键。</param>
/// <returns>键 <paramref name="key"/> 对应的值，不存在则返回 <c>default(Value)</c>。</returns>
public TValue Get(TKey key)
{
    var indices = Get(key, _root);
    if (indices == -1)
    {
        return default;
    }

    return _nodes[indices].Value;
}

/// <summary>
/// 获取 <paramref name="key"/> 对应的下标，不存在则返回 -1。
/// </summary>
/// <param name="key">键。</param>
/// <param name="start">起始搜索下标。</param>
/// <returns>找到则返回对应下标，否则返回 -1。</returns>
private int Get(TKey key, int start)
{
    var now = start;
    while (now != -1)
    {
        var cmp = _nodes[now].Key.CompareTo(key);
        if (cmp > 0)
        {
            now = _left[now];
        }
        else if (cmp < 0)
        {
            now = _right[now];
        }
        else
        {
            return now;
        }
    }

    return -1;
}

/// <summary>
/// 从表中删去键 <paramref name="key"/> 及其对应的值。
/// </summary>
/// <param name="key">要删除的键。</param>
public void Delete(TKey key)
{
    var toDelete = Get(key, _root);
    if (toDelete == -1)
    {
        throw new InvalidOperationException("No Such Key in BST");
    }

    _root = Delete(key, _root);
    RemoveNode(toDelete);
}

/// <summary>
/// 从根结点为 <paramref name="root"/> 的二叉搜索树中删除键为 <paramref name="key"/> 的结点。
/// 返回删除结点后树的根结点下标。
/// </summary>
/// <param name="key">要删除的键。</param>
/// <param name="root">根结点。</param>
/// <returns>删除结点后树的根结点下标。</returns>
private int Delete(TKey key, int root)
{
    if (root == -1 || _nodes[root] == null)
    {
        return -1;
    }

    var cmp = _nodes[root].Key.CompareTo(key);
    if (cmp > 0)
    {
        _left[root] = Delete(key, _left[root]);
    }
    else if (cmp < 0)
    {
        _right[root] = Delete(key, _right[root]);
    }
    else
    {
        if (_left[root] == -1)
        {
            return _right[root];
        }

        if (_right[root] == -1)
        {
            return _left[root];
        }

        var toReplace = Min(_right[root]);
        _right[toReplace] = DeleteMin(_right[root]);
        _left[toReplace] = _left[root];
        root = toReplace;
    }

    return root;
}

/// <summary>
/// 键 <paramref name="key"/> 在表中是否存在对应的值。
/// </summary>
/// <param name="key">键。</param>
/// <returns>如果存在则返回 <c>true</c>，否则返回 <c>false</c>。</returns>
public bool Contains(TKey key)
{
    return Get(key, _root) > -1;
}

/// <summary>
/// 符号表是否为空。
/// </summary>
/// <returns>为空则返回 <c>true</c>，否则返回 <c>false</c>。</returns>
public bool IsEmpty()
{
    return _size == 0;
}

/// <summary>
/// 获得符号表中键值对的数量。
/// </summary>
/// <returns>符号表中键值对的数量。</returns>
public int Size()
{
    return _size;
}

/// <summary>
/// [<paramref name="lo"/>, <paramref name="hi"/>] 之间键的数量。
/// </summary>
/// <param name="lo">范围起点。</param>
/// <param name="hi">范围终点。</param>
/// <returns>[<paramref name="lo"/>, <paramref name="hi"/>] 之间键的数量。</returns>
public int Size(TKey lo, TKey hi)
{
    return Keys(lo, hi).Count();
}

/// <summary>
/// 计算以 <paramref name="root"/> 为根结点的二叉树的大小。
/// </summary>
/// <param name="root">二叉树的根结点下标。</param>
/// <returns>二叉树中的结点个数。</returns>
private int Size(int root)
{
    if (root == -1)
    {
        return 0;
    }

    return 1 + Size(_left[root]) + Size(_right[root]);
}

/// <summary>
/// 获得符号表中所有键的集合。
/// </summary>
/// <returns>符号表中所有键的集合。</returns>
public IEnumerable<TKey> Keys()
{
    if (IsEmpty())
    {
        return new List<TKey>();
    }
    return Keys(Min(), Max());
}

/// <summary>
/// 获得符号表中 [<paramref name="lo"/>, <paramref name="hi"/>] 之间的键。
/// </summary>
/// <param name="lo">范围起点。</param>
/// <param name="hi">范围终点。</param>
/// <returns>符号表中 [<paramref name="lo"/>, <paramref name="hi"/>] 之间的键。</returns>
public IEnumerable<TKey> Keys(TKey lo, TKey hi)
{
    if (lo == null)
        throw new ArgumentNullException("first argument to keys() is null");
    if (hi == null)
        throw new ArgumentNullException("second argument to keys() is null");

    var queue = new Queue<TKey>();
    Keys(_root, queue, lo, hi);
    return queue;
}

/// <summary>
/// 获取二叉查找树中在 <paramref name="lo"/> 和 <paramref name="hi"/> 之间的所有键。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <param name="queue">要填充的队列。</param>
/// <param name="lo">键的下限。</param>
/// <param name="hi">键的上限。</param>
private void Keys(int x, Queue<TKey> queue, TKey lo, TKey hi)
{
    if (x == -1)
    {
        return;
    }

    var cmplo = lo.CompareTo(_nodes[x].Key);
    var cmphi = hi.CompareTo(_nodes[x].Key);
    if (cmplo < 0)
    {
        Keys(_left[x], queue, lo, hi);
    }

    if (cmplo <= 0 && cmphi >= 0)
    {
        queue.Enqueue(_nodes[x].Key);
    }

    if (cmphi > 0)
    {
        Keys(_right[x], queue, lo, hi);
    }
}

/// <summary>
/// 最小的键。
/// </summary>
/// <returns>最小的键。</returns>
public TKey Min()
{
    if (IsEmpty())
    {
        throw new InvalidOperationException("BST is Empty!");
    }

    return _nodes[Min(_root)].Key;
}

/// <summary>
/// 在二叉查找树中查找包含最小键的结点。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <returns>包含最小键的结点。</returns>
private int Min(int x)
{
    if (_left[x] == -1)
    {
        return x;
    }

    return Min(_left[x]);
}

/// <summary>
/// 最大的键。
/// </summary>
/// <returns>最大的键。</returns>
public TKey Max()
{
    if (IsEmpty())
    {
        throw new InvalidOperationException("BST is Empty!");
    }

    return _nodes[Max(_root)].Key;
}

/// <summary>
/// 在二叉查找树中查找包含最大键的结点。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <returns>包含最大键的结点。</returns>
private int Max(int x)
{
    if (_right[x] == -1)
    {
        return x;
    }

    return Max(_right[x]);
}

/// <summary>
/// 小于等于 <paramref name="key"/> 的最大值。
/// </summary>
/// <returns>小于等于 <paramref name="key"/> 的最大值。</returns>
public TKey Floor(TKey key)
{
    if (key == null)
    {
        throw new ArgumentNullException("argument to floor is null");
    }

    if (IsEmpty())
    {
        throw new InvalidOperationException("calls floor with empty symbol table");
    }
    var x = Floor(_root, key);
    if (x == -1)
    {
        return default;
    }
    else
    {
        return _nodes[x].Key;
    }
}

/// <summary>
/// 获得符号表中小于等于 <paramref name="key"/> 的最大结点。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <param name="key">键。</param>
/// <returns>小于等于 <paramref name="key"/> 的最大结点。</returns>
private int Floor(int x, TKey key)
{
    if (x == -1)
    {
        return -1;
    }
    var cmp = key.CompareTo(_nodes[x].Key);
    if (cmp == 0)
    {
        return x;
    }
    else if (cmp < 0)
    {
        return Floor(_left[x], key);
    }
    var t = Floor(_right[x], key);
    if (t != -1)
    {
        return t;
    }

    return x;
}

/// <summary>
/// 大于等于 <paramref name="key"/> 的最小值。
/// </summary>
/// <returns>大于等于 <paramref name="key"/> 的最小值。</returns>
public TKey Ceiling(TKey key)
{
    if (key == null)
    {
        throw new ArgumentNullException("argument to ceiling is null");
    }

    if (IsEmpty())
    {
        throw new InvalidOperationException("calls ceiling with empty symbol table");
    }
    var x = Ceiling(_root, key);
    if (x == -1)
    {
        return default;
    }
    return _nodes[x].Key;
}

/// <summary>
/// 获取符号表中大于等于 <paramref name="key"/> 的最小结点。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <param name="key">键。</param>
/// <returns>符号表中大于等于 <paramref name="key"/> 的最小结点。</returns>
private int Ceiling(int x, TKey key)
{
    if (x == -1)
    {
        return -1;
    }
    var cmp = key.CompareTo(_nodes[x].Key);
    if (cmp == 0)
    {
        return x;
    }
    if (cmp < 0)
    {
        var t = Ceiling(_left[x], key);
        if (t != -1)
        {
            return t;
        }
        return x;
    }
    return Ceiling(_right[x], key);
}

/// <summary>
/// 小于 <paramref name="key"/> 的键的数量。
/// </summary>
/// <returns>小于 <paramref name="key"/> 的键的数量。</returns>
public int Rank(TKey key)
{
    if (key == null)
    {
        throw new ArgumentNullException("argument to rank() is null");
    }
    return Rank(_root, key);
}

/// <summary>
/// 返回 <paramref name="key"/> 在二叉查找树中的排名。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <param name="key">要查找排名的键。</param>
/// <returns><paramref name="key"/> 的排名。</returns>
private int Rank(int x, TKey key)
{
    if (x == -1)
    {
        return 0;
    }
    var cmp = key.CompareTo(_nodes[x].Key);
    if (cmp < 0)
    {
        return Rank(_left[x], key);
    }
    else if (cmp > 0)
    {
        return 1 + Size(_left[x]) + Rank(_right[x], key);
    }
    else
    {
        return Size(_left[x]);
    }
}

/// <summary>
/// 获得排名为 k 的键。
/// </summary>
/// <param name="k">需要获得的键的排名。</param>
/// <returns>排名为 k 的键。</returns>
public TKey Select(int k)
{
    if (k < 0 || k >= Size())
    {
        throw new ArgumentException("argument to select() is invaild: " + k);
    }
    var x = Select(_root, k);
    return _nodes[x].Key;
}

/// <summary>
/// 挑拣出排名为 <paramref name="k"/> 的结点。
/// </summary>
/// <param name="x">树的根结点。</param>
/// <param name="k">要挑拣的排名。</param>
/// <returns>排名为 <paramref name="k"/> 的结点。</returns>
private int Select(int x, int k)
{
    if (x == -1)
    {
        return -1;
    }
    var t = Size(_left[x]);
    if (t > k)
    {
        return Select(_left[x], k);
    }
    else if (t < k)
    {
        return Select(_right[x], k - t - 1);
    }
    else
    {
        return x;
    }
}

/// <summary>
/// 删除最小的键。
/// </summary>
public void DeleteMin()
{
    if (IsEmpty())
    {
        throw new InvalidOperationException("Symbol table underflow");
    }

    var minIndex = Min(_root);
    _root = DeleteMin(_root);
    RemoveNode(minIndex);
}

/// <summary>
/// 在以 <paramref name="x"/> 为根结点的二叉查找树中删除最小结点。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <returns>删除后的二叉查找树。</returns>
private int DeleteMin(int x)
{
    if (_left[x] == -1)
    {
        return _right[x];
    }

    _left[x] = DeleteMin(_left[x]);
    return x;
}

/// <summary>
/// 删除最大的键。
/// </summary>
public void DeleteMax()
{
    if (IsEmpty())
    {
        throw new InvalidOperationException("Symbol table underflow");
    }

    var maxIndex = Max(_root);
    _root = DeleteMax(_root);
    RemoveNode(maxIndex);
}

/// <summary>
/// 从指定二叉查找树中删除最大结点。
/// </summary>
/// <param name="x">二叉查找树的根结点。</param>
/// <returns>删除后的二叉查找树。</returns>
private int DeleteMax(int x)
{
    if (_right[x] == -1)
        return _left[x];
    _right[x] = DeleteMax(_right[x]);
    
    return x;
}

/// <summary>
/// 删除下标为 <paramref name="index"/> 的结点。
/// </summary>
/// <param name="index">要删除的结点下标。</param>
private void RemoveNode(int index)
{
    _size--;
    // Remove Node
    for (var i = index; i < _size; i++)
    {
        _nodes[i] = _nodes[i + 1];
        _left[i] = _left[i + 1];
        _right[i] = _right[i + 1];
    }
    // Adjust Index
    if (_root >= index)
    {
        _root--;
    }
    for (var i = 0; i < _size; i++)
    {
        if (_left[i] >= index)
        {
            _left[i]--;
        }

        if (_right[i] >= index)
        {
            _right[i]--;
        }
    }
}

另请参阅

BinarySearchTree 库

3.2.42

解答

按照题意实现即可，关键点有两个：

一是选择前驱的实现方式，只要选择左子树中的最大结点即可。

if (_random.NextDouble() < 0.5)
{
    x = Min(t.Right);
    x.Right = DeleteMin(t.Right);
    x.Left = t.Left;
}
else
{
    x = Max(t.Left);
    x.Left = DeleteMax(t.Left);
    x.Right = t.Right;
}

二是内部路径长度的计算方式，需要用层序遍历把所有结点的深度加起来。

var internalPath = 0;
var nowLayer = new Queue<Node>();
var nextLayer = new Queue<Node>();
nextLayer.Enqueue(root);

var depth = 0;
while (nextLayer.Count > 0)
{
    var temp = nowLayer;
    nowLayer = nextLayer;
    nextLayer = temp;

    while (nowLayer.Count > 0)
    {
        var node = nowLayer.Dequeue();
        if (node.Left != null)
        {
            nextLayer.Enqueue(node.Left);
        }

        if (node.Right != null)
        {
            nextLayer.Enqueue(node.Right);
        }

        internalPath += depth;
    }

    depth++;
}

return internalPath;

结果如下：

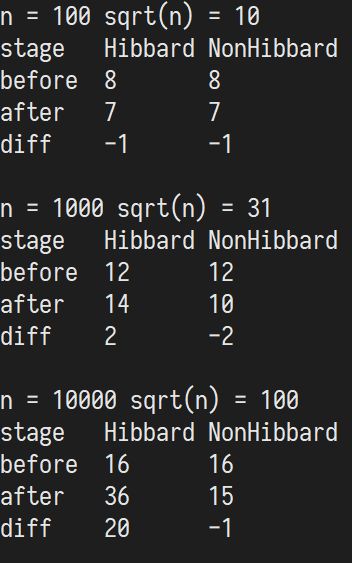
另请参阅

BinarySearchTree 库

3.2.43

解答

依照题意实现即可，put/get 大约 10 倍差距。

MostFrequentlyKey 的实现：

public static TKey MostFrequentlyKey<TKey>(IST<TKey, int> st, TKey[] keys)
{
    foreach (var s in keys)
    {
        if (st.Contains(s))
            st.Put(s, st.Get(s) + 1);
        else
            st.Put(s, 1);
    }

    var max = keys[0];
    foreach (var s in st.Keys())
        if (st.Get(s) > st.Get(max))
            max = s;

    return max;
}

另请参阅

BinarySearchTree 库

3.2.44

解答

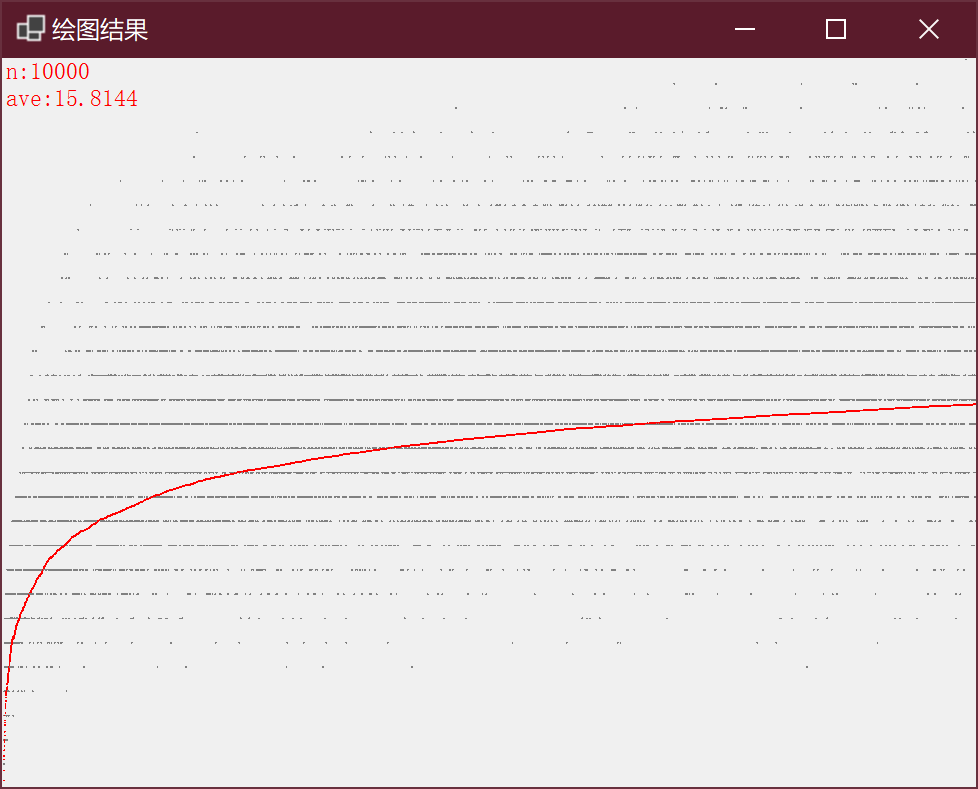
使用类似于 3.1.38 的方法进行绘图，当 n=10000 时的结果如下：

代码

绘图部分：

public void Draw(long[] data)
{
    var panel = CreateGraphics();
    var unitX = (float)ClientRectangle.Width / data.Length;
    var unitY = (float)ClientRectangle.Height / data.Max();

    var accumulation = 0f;  // f = float
    for (var i = 0; i < data.Length; i++)
    {
        // Gray
        panel.FillEllipse(Brushes.Gray, (i + 1) * unitX, ClientRectangle.Bottom - data[i] * unitY, 2, 2);
        // Red
        panel.FillEllipse(Brushes.Red, (i + 1) * unitX, ClientRectangle.Bottom - accumulation / (i + 1) * unitY, 2, 2);
        accumulation += data[i];
    }

    panel.DrawString($"n:{data.Length}\nave:{accumulation / data.Length}", SystemFonts.DefaultFont, Brushes.Red, 0, 0);
}

测试部分：

private long[] Test(int n)
{
    var testCases = new long[n];
    var testResult = new long[n];
    for (var i = 0; i < n; i++)
    {
        testCases[i] = i;
    }
    Shuffle(testCases);

    var bst = new BSTAnalysis<long, int>();
    for (var i = 0; i < n; i++)
    {
        bst.CompareTimes = 0;
        bst.Put(testCases[i], 1);
        testResult[i] = bst.CompareTimes;
    }

    return testResult;
}

static void Shuffle<T>(T[] a)
{
    var random = new Random();
    for (var i = 0; i < a.Length; i++)
    {
        var r = i + random.Next(a.Length - i);
        var temp = a[i];
        a[i] = a[r];
        a[r] = temp;
    }
}

另请参阅

BinarySearchTree 库

3.2.45

解答

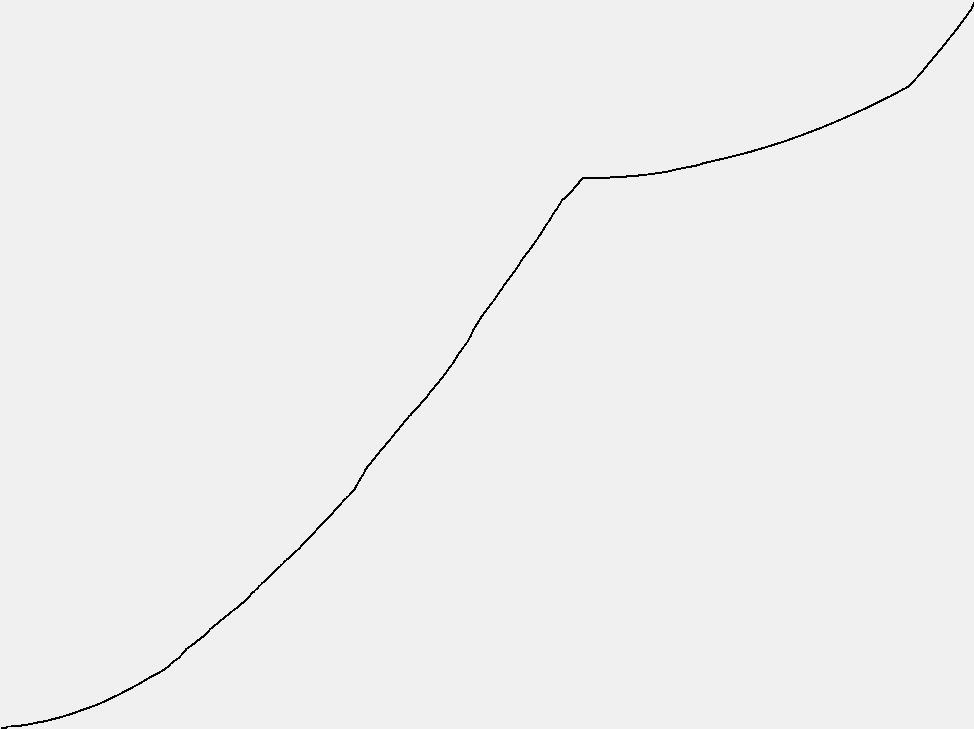
结果如下，可参考 3.1.39。

SequentialSearchST

BinarySearchST

BST

可以看到 BST 的曲线更为平滑，插入和查找部分耗时十分接近。

另请参阅

BinarySearchTree 库

3.2.46

解答

翻译有些问题，其实指的是用 N 个 double 构造一个 BST 和 BinarySearchST 的速度对比。
Get 速度 BST 是不会比 BinarySearchST 快的。（$1.39\lg N$ > $\lg N$）

二叉搜索树一次查找平均需要 $1.39\lg N$ 次比较，二分查找则是 $N/2$，于是可以求得开销：
二叉查找树：$1.39 \sum_{i=1}^{N-1} \lg i=1.39 \lg (N-1)!=1.39(N-1)\lg(N-1)$。
二分查找实现的符号表：$1/2+2/2+ \cdots+(N-1)/2=N(N-1)/4$ 。
令两式相等，可以求得快 10 倍，100 倍，1000 倍的 $N$ 值。
例如快 10 倍的方程：

\[13.9(N-1)\lg(N-1)=N(N-1)/4 \\ 13.9\lg (N-1)=N/4 \]

这是一个超越方程，可以简单用程序穷举出一个数值解。

for (var i = 0d; i < int.MaxValue; i++)
{
    if (13.9 * Math.Log2(i - 1) < i / 4)
    {
        Console.WriteLine(i);
        return;
    }
}

解得的三个 N 值分别为 499，7115，91651。

除了基本的新元素赋值外，二叉树在插入时只需要进行比较即可。
但二分查找实现的符号表还需要维持数组有序，需要额外的赋值操作。
因此二分查找实现的符号表和二叉搜索树的开销如下：

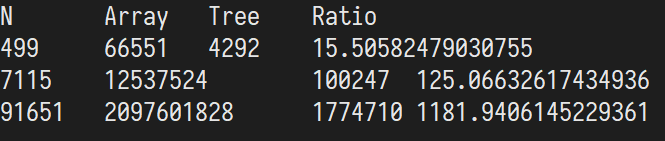
其中 Array 包含了比较和额外的赋值次数，Tree 只有比较次数。

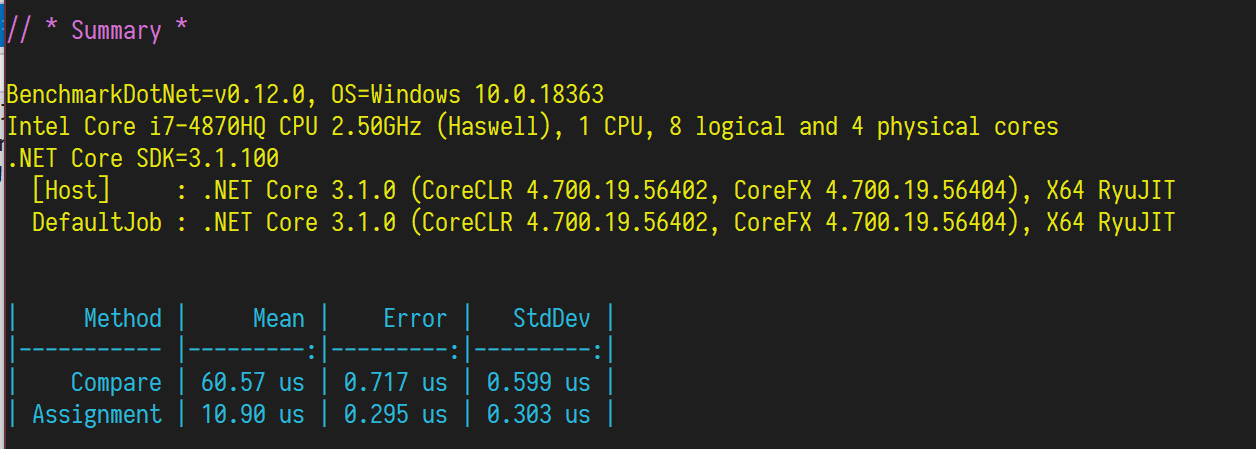
一般我们认为比较（Compare）和赋值（=）开销是一样的，但实际上比较会慢 6 倍左右（.net core 3.1），因此如果直接进行计时测试，可能得不出快 10 倍/100 倍/1000 倍的结果。

另请参阅

BinarySearchTree 库

3.2.47

解答

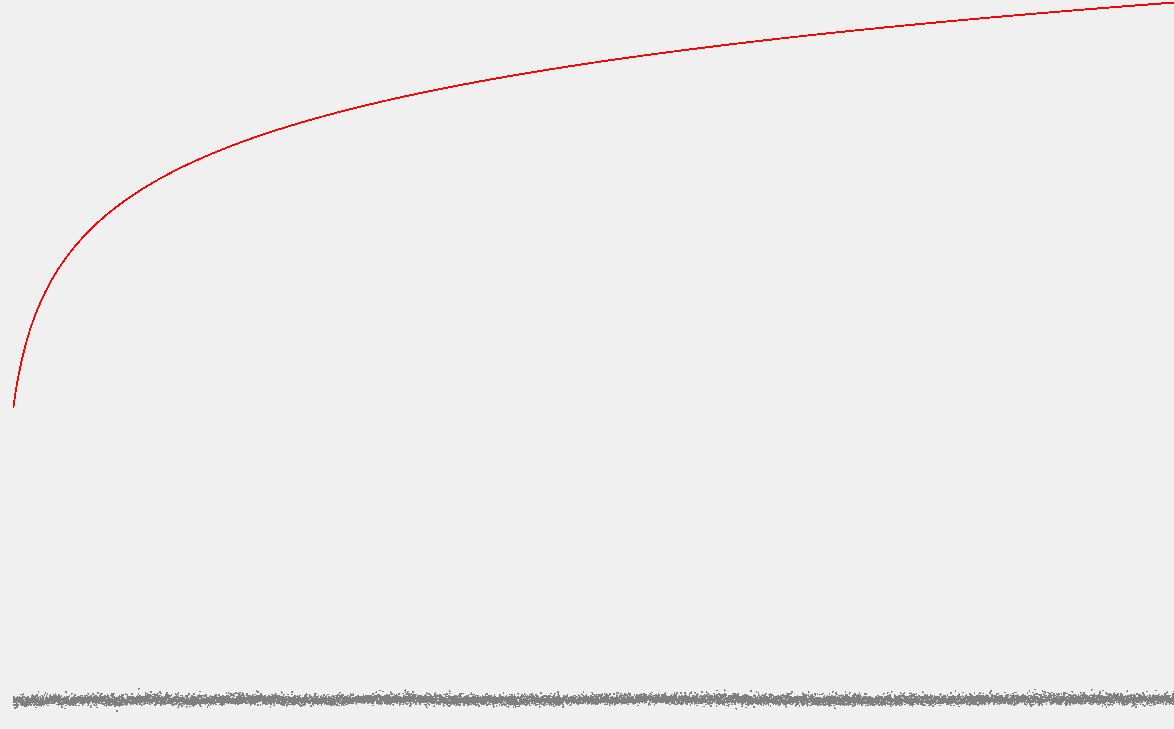
如下图所示，内部路径平均长度是比较符合规律的：

方差：

代码

一次测试：

private int Test(int n)
{
    var data = GetRandomInt(n);
    var bst = new BST<int, int>();
    foreach (var d in data)
    {
        bst.Put(d, d);
    }

    return bst.AverageInternalPathLength();
}

求解内部路径长度：

public int AverageInternalPathLength() => InternalPath() / Size() + 1;

private int InternalPath()
{
    var internalPath = 0;
    var nowLayer = new Queue<Node>();
    var nextLayer = new Queue<Node>();
    nextLayer.Enqueue(root);

    var depth = 0;
    while (nextLayer.Count > 0)
    {
        var temp = nowLayer;
        nowLayer = nextLayer;
        nextLayer = temp;

        while (nowLayer.Count > 0)
        {
            var node = nowLayer.Dequeue();
            if (node.Left != null)
            {
                nextLayer.Enqueue(node.Left);
            }

            if (node.Right != null)
            {
                nextLayer.Enqueue(node.Right);
            }

            internalPath += depth;
        }

        depth++;
    }

    return internalPath;
}

另请参阅

BinarySearchTree 库

posted @ 2020-08-04 10:36 沈星繁阅读(499) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

沈星繁

青

算法（第四版）C# 习题题解——3.2

写在前面

习题&题解

解答

另请参阅

解答

解答

解答

解答

另请参阅

解答

解答

解答

代码

解答

另请参阅

解答

解答

解答

解答

另请参阅

解答

代码

另请参阅

解答

解答

另请参阅

解答

解答

解答

解答

解答

另请参阅

解答

解答

另请参阅

解答

解答

另请参阅

解答

解答

解答

代码

另请参阅

解答

代码

另请参阅

解答

代码

另请参阅

解答

代码

另请参阅

解答

代码

另请参阅

解答

代码

另请参阅

解答

代码

另请参阅

解答

解答

代码

另请参阅

解答

代码

另请参阅

解答

代码

解答

代码

另请参阅

解答

代码

另请参阅

解答