插入排序

1.概念

插入排序(InsertionSort)，一般也被称为直接插入排序。

对于少量元素的排序，它是一个有效的算法。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增 1 的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

插入排序是一种很简单的排序方法，就像我们整理书桌上的书一样。想象一下，你已经有了一堆按顺序排列好的书，现在又拿到一本新的书，你就会从头开始找，看看这本新书应该插在哪个位置，然后把后面的书都往后挪一挪，最后把新书放进去，这样书就还是按顺序排列的啦。

在插入排序里，我们把数组看成两部分，前面是已经排好序的有序部分，后面是还没排好的部分。每次我们从没排好的部分拿出一个数，然后把它插入到前面有序部分的合适位置，就像刚才放书一样。外层循环是遍历没排好的部分，内层循环是找插入位置并且移动元素。

笔记关键词：插入排序，简单，类似整理书，有序部分，无序部分，外层循环，内层循环，找位置，移动元素。

2.说明

插入排序的平均时间复杂度也是 O(n^2)，空间复杂度为常数阶 O(1)，具体时间复杂度和数组的有序性也是有关联的。

插入排序中，当待排序数组是有序时，是最优的情况，只需当前数跟前一个数比较一下就可以了，这时一共需要比较 N-1 次，时间复杂度为 O(N)。最坏的情况是待排序数组是逆序的，此时需要比较次数最多，最坏的情况是 O(n^2)。

插入排序的时间复杂度听起来有点复杂，但其实很好理解。我们可以把时间复杂度想象成完成排序任务需要花费的“力气”。插入排序的平均情况是 O(n²)，这就好比大部分时候，我们要花费中等的力气来完成排序。

不过，如果数组已经是有序的，比如从小到大排好了，那插入排序就会变得超级轻松！因为每个数字只需要和前面的数字比较一下，看看是不是已经排好了，根本不需要移动。这种情况下，我们只需要用很少的力气，也就是 O(N) 的时间复杂度，就能完成排序啦。

反过来，如果数组是完全逆序的，比如从大到小排好，那插入排序就会变得很费劲。因为每个数字都需要和前面很多数字比较，还要移动很多次，这时候就需要花费最多的力气，时间复杂度就是 O(n²)。

总结一下笔记：插入排序，时间复杂度，平均 O(n²)，有序时 O(N)，逆序时 O(n²)。

3.图示

假设前面 n-1(其中 n>=2)个数已经是排好顺序的，现将第 n 个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。

按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序。

从小到大的插入排序整个过程如图示：

第一轮：从第二位置的 6 开始比较，比前面 7 小，交换位置。

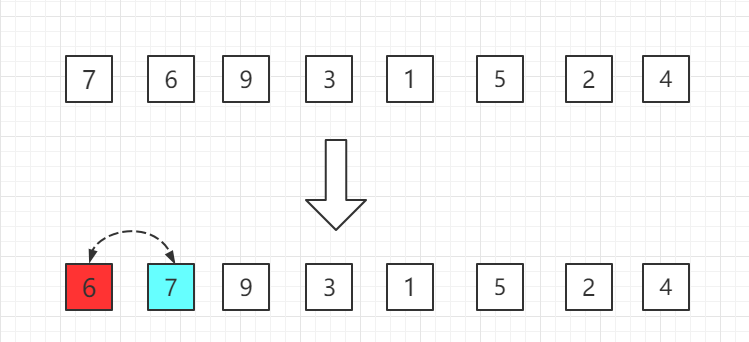
 第二轮：第三位置的 9 比前一位置的 7 大，无需交换位置。

 第三轮：第四位置的 3 比前一位置的 9 小交换位置，依次往前比较。

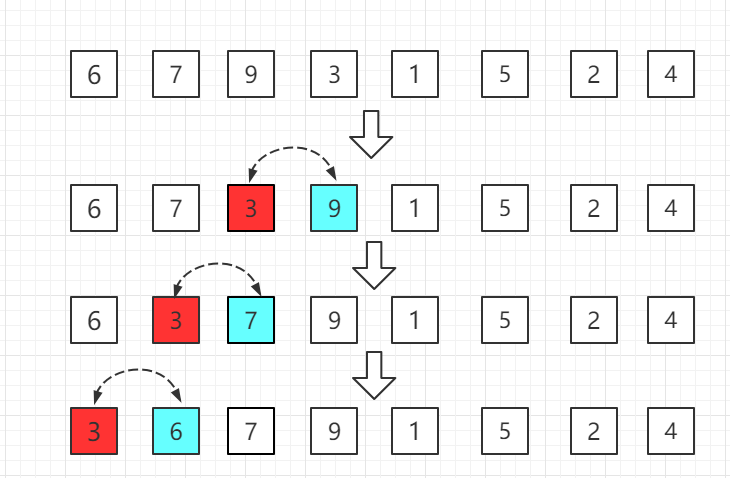
 第四轮：第五位置的 1 比前一位置的 9 小，交换位置，再依次往前比较。

......

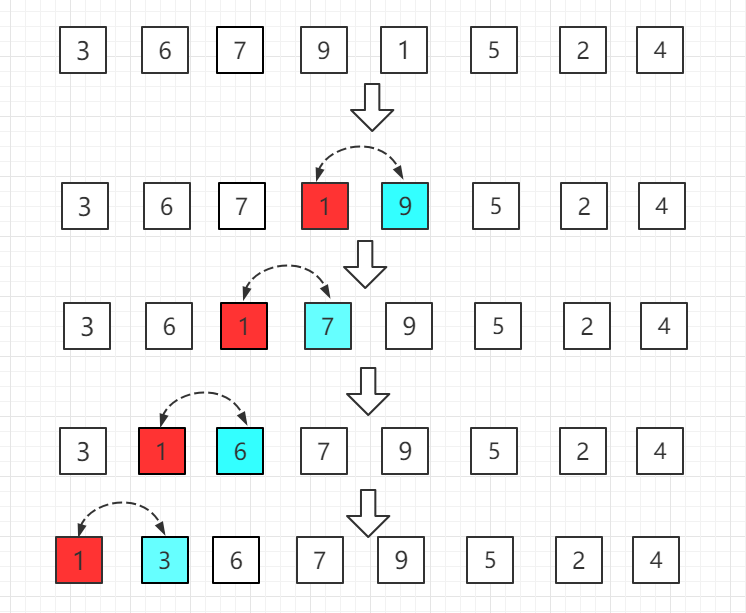
就这样依次比较到最后一个元素。

4.代码