新型AI架构BriLLM的数学原理与代码示例
本文由 愚人猫(Idiomeo) 编写
推荐阅读我的博客原文,排版更好
类脑AI架构BriLLM的介绍
在当前的大语言模型领域,Transformer 架构已经成为绝对主流,支撑着 GPT、BERT 等众多强大的语言模型。然而,这种基于注意力机制的架构存在着一些根本性的局限:黑箱不透明性、二次方复杂度以及上下文长度依赖等问题。上海交通大学赵海教授团队于 2025 年 3 月提出的 BriLLM (Brain-inspired Large Language Model) 彻底颠覆了这一范式,它是首个在宏观尺度上模拟人脑全局机制的大语言模型,对机器学习范式进行了颠覆性创新。
BriLLM 不基于 Transformer、不基于 GPT、也不基于传统的输入输出控制的生成语言模型框架。相反,它建立在一种全新的学习机制 —— 信号全连接流动 (Signal Fully-connected Flowing, SiFu) 之上,这种机制定义在有向图上,赋予了整个模型所有节点完全的可解释性,而不是像传统机器学习模型那样仅在输入和输出端有有限的可解释性。
本文将带你了解 BriLLM 的底层数学原理、技术实现以及与传统 Transformer 架构的本质区别,帮助你理解这一新型AI架构。
BriLLM 的理论基础与数学原理
传统语言模型的局限性
在理解 BriLLM 的创新之前,我们需要先回顾传统语言模型的局限性。传统的生成式语言模型,如 GPT 系列,主要基于 Transformer 架构,采用自回归预测的方式。对于一个输入序列
,模型需要预测下一个 token$w_i$,其数学表达式可以表示为:
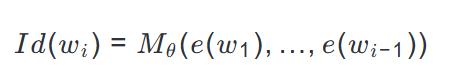
其中,Id()表示 token 的输出表示 (通常是 one-hot 向量),e()表示输入表示 (通常称为词向量),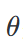
是模型需要学习的参数集合。
当引入注意力机制后,模型变为:
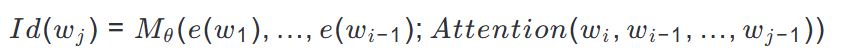
这些模型的局限性在于:
- 解释性局限:只有输入序列
![image]()
和输出w_i是直接可理解的;模型$M$及其参数$\theta$需要专门的分析才能阐明它们在学习过程中的作用。 - 模型规模与输入长度关联:模型大小与输入上下文长度相关,因为$M$必须通过唯一的输入端口处理整个序列
![image]()
。 - 平方复杂度:Transformer 的自注意力机制本质上具有平方级别的时间与空间复杂度 O (n²),处理更长的上下文时,计算开销将随输入长度的平方增长。
BriLLM 的核心创新:SiFu 机制
BriLLM 的核心创新在于其独创的 "信号全连接流动"(Signal Fully-connected Flowing, SiFu) 学习机制。这一机制在一个有向图上进行定义,旨在模拟大脑中的电生理信息流。
形式化地说,SiFu 是为词汇表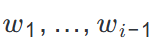
定义的,其中节点V = {v_1, ..., v_n}(每个v_i映射到w_i)。节点v_i和v_j之间的边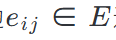
通过可学习参数控制信号传输。信号张量r从对应输入 token 的节点开始,并通过图传播,节点处的变换 (()) 和边处的变换 (()) 由可学习参数$\theta_V$(节点) 和$\theta_E$(边) 决定。
在 SiFu 机制中,给定输入 
(映射到v_1, ..., v_{i-1}),信号$r$通过这些节点传播。下一个 token-w_i被识别为信号能量最大的节点v_i,计算方式为:
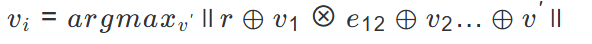
对于自回归预测 (如 GPT),相应的最大能量计算为:
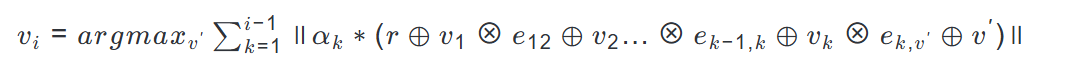
其中alpha_k是可学习权重,使模型能够 "关注" 相关的先前节点,模仿分布式神经整合。
信号传播的数学模型
BriLLM 中的信号传播过程可以用以下数学模型描述:
信号传播开始于初始张量:
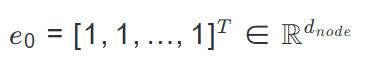
对于序列u_1, ..., u_{L-1},v_{predict},从u_i传播到u_{i+1}的信号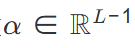
定义为:
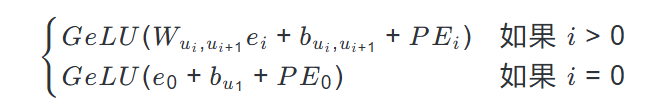
这里,位置编码 (PE) 确保序列顺序得以保留,而边特定的偏置调节信号强度。
为了预测下一个 token,BriLLM 使用可学习权重$\alpha \in \mathbb{R}^{L-1}$整合来自所有先前节点的信号:
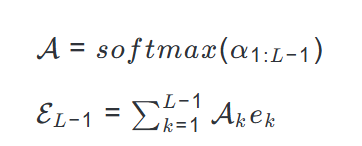
其中$\mathcal{A}$被 softmax 归一化以优先考虑相关信号。最终预测是使传播信号能量最大化的节点:
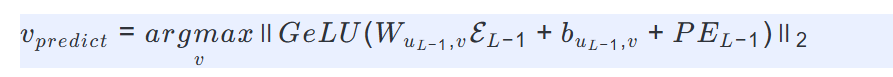
基于能量最大化的学习机制
BriLLM 的学习过程基于能量最大化原则,类似于认知过程中的神经通路强化。信号传播遵循 "最小阻力原则",沿着能量最大化的路径流动。
这一过程可以形式化地表示为寻找信号传播路径,使得以下能量函数最大化:
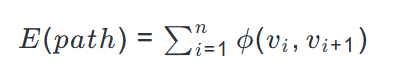
其中$\phi(v_i, v_{i+1})$是节点$v_i$到$v_{i+1}$的转移能量,由边参数$W_{v_i, v_{i+1}}$和节点参数$b_{v_i}$决定。
在训练过程中,模型通过调整参数$\theta_V$和$\theta_E$来最大化正确路径的能量,最小化错误路径的能量。这与传统的基于交叉熵损失的训练方法有本质区别,更接近大脑中神经通路的强化过程。
BriLLM 的技术实现与架构分析
图结构设计
BriLLM 通过有向图$G={V,E}$实现 SiFu 学习:
- 节点 (V):显式映射到 tokens,对应特定语义的皮层区域。每个节点使用 GeLU 激活的神经元层,包含偏置项,维度为$d_{node}$。
- 边 (E):启用双向信号传输,模拟神经电生理活动。节点间的双向连接矩阵维度为$d_{node} \times d_{node}$。
BriLLM 的一个关键创新是其节点与 token 的显式映射。在 BriLLM 中,每个 token 都被明确地映射到图中的一个节点,这种静态语义映射确保了模型的每个组件都具有明确的语义解释,实现了完全的可解释性,不再是传统深度学习的黑盒模型。
信号传播机制实现
BriLLM 的信号传播机制实现了动态信号传播,模拟电生理信息流动,信号沿 "最小阻力" 路径流动。这一过程通过以下步骤实现:
- 信号初始化:信号传播开始于初始张量$e_0 = [1, 1, ..., 1]^T \in \mathbb{R}^{d_{node}}$。
- 位置编码整合:使用正弦余弦位置编码确保序列顺序信息的保留。位置编码$PE_i$被添加到信号中,以保持序列顺序。
- 节点到节点的信号转换:信号通过边权重矩阵$W_{u_i, u_{i+1}}$和节点偏置$b_{u_i, u_{i+1}}$进行转换,然后应用 GeLU 激活函数。
- 信号整合与预测:在预测步骤,来自所有先前节点的信号通过可学习权重$\alpha$进行整合,最终预测是使信号能量最大化的节点。
与 Transformer 的架构对比
BriLLM 与传统 Transformer 架构在多个关键方面存在本质区别:
- 模型解释性:
- Transformer:只有输入和输出是可解释的,内部机制难以理解。
- BriLLM:完全模型可解释性。每个节点映射到一个 token,使得语义处理在所有层次上都是透明的 —— 复制了大脑的分布式解释性。
- 上下文长度处理:
- Transformer:模型大小随输入上下文长度增长,因为$M$必须通过唯一的输入端口处理整个序列$w_1, ..., w_{i-1}$。
- BriLLM:无界上下文处理。像大脑一样,SiFu 处理任意长的序列而不扩展其结构,因为信号传播而非参数缩放处理更长的输入。
- 信号传播机制:
- Transformer:依赖注意力机制。
- BriLLM:动态信号传播。边$E$启用双向信号传输,模仿神经电生理学。
- 多模态兼容性:
- Transformer:输入 / 输出对齐。
- BriLLM:固有多模态兼容性。由于节点可以表示任何语义单元,而不仅仅是语言。
- 错误溯源:
- Transformer:模糊的 (例如,注意力)。
- BriLLM:认知可追踪性。由于信号传播和预测激活跨越可解释节点,动态预测行为在整个过程中是可解释的,实现认知可追踪性。错误生成可以定位到特定的信号路径 (例如,具有异常激活的节点或边),类似于通过神经成像分析异常脑活动。
| 特性 | 传统 LLM | BriLLM |
|---|---|---|
| 模型架构基础 | Transformer、循环网络等 | 有向图结构 |
| 核心机制 | 注意力机制 | 信号全连接流动 (SiFu) |
| 计算复杂度 | 与输入长度成二次方关系 O (n²) | 与输入长度无关 O (1) |
| 模型规模与输入关系 | 模型大小与输入上下文长度相关 | 模型大小与输入上下文长度无关 |
| 可解释性 | 仅输入输出可解释 | 所有节点和边可解释 |
| 多模态支持 | 附加组件或输入输出对齐 | 固有支持,自然集成 |
| 训练数据需求 | 大量数据 | 可能需要较少数据(生物合理性) |
| 理论基础 | 统计学习理论 | 神经认知原理 |
稀疏训练与模型压缩
BriLLM 利用 "低频词元边共享" 的方法,让参数规模降低 90%:大多数二元组 (bigram) 很少出现甚至未出现,因此允许对不活跃边共享参数。对于这些低频二元组,采用一个固定且不更新的矩阵,从而将模型大小缩减至中文版本约 20 亿参数、英文版约 10 亿参数,分别仅占原模型规模的 13.0% 和 5.7%。
这一技术受到大脑神经通路复用的启发,不仅减少了参数量近 90%,同时也显著加速了训练过程。
多模态扩展能力
BriLLM 的 "节点 - 信号" 设计以及全模型可解释性天生支持多模态融合:模型中的节点不仅限于表示语言 token,还可以映射多种模态的单元。引入新模态时,只需为其定义对应的节点,无需从头训练模型 —— 这与依赖输入 / 输出界面对齐的传统大语言模型截然不同。
具体来说,BriLLM 的多模态扩展可以通过以下方式实现:
- 添加视觉节点:直接处理图像语义
- 添加听觉节点:整合声音信号流
- 添加具身交互节点:环境输入与实时驱动信号传播
这种多模态支持是内在的,而非附加的,体现了 BriLLM 架构的灵活性和生物合理性。
BriLLM 的 Golang 实现示例
由于 BriLLM 是一个全新的架构,目前官方实现主要以 Python 为主。不过,基于其数学原理和架构描述,我们可以尝试用 Golang 实现其核心机制的简化版本,以展示其工作原理。
节点与边结构定义
首先,我们定义节点和边的结构:
package main
import (
"math/rand"
"gonum.org/v1/gonum/mat"
)
// Node 表示图中的节点,对应一个token
type Node struct {
id int // 节点ID
embedding \*mat.Dense // 节点的嵌入向量
bias \*mat.Dense // 节点偏置
}
// Edge 表示节点之间的边
type Edge struct {
from int
to int
weight \*mat.Dense // 边的权重矩阵
}
// Graph 表示整个BriLLM图结构
type Graph struct {
nodes \[]\*Node
edges map\[string]\*Edge // 用"from-to"字符串作为键
}
信号传播实现
接下来,实现信号传播函数:
// propagateSignal 计算信号从当前节点传播到下一个节点的结果
func propagateSignal(currentSignal \*mat.Dense, edge \*Edge, nextNode \*Node, positionEncoding \*mat.Dense) \*mat.Dense {
// 计算边的变换:W \* currentSignal
edgeTransform := mat.NewDense(edge.weight.Rows(), edge.weight.Cols(), nil)
edgeTransform.Mul(edge.weight, currentSignal)
// 添加边的偏置(如果有的话)
// 这里假设边没有偏置,偏置在节点中处理
// 添加位置编码
signalWithPE := mat.NewDense(edgeTransform.Rows(), edgeTransform.Cols(), nil)
signalWithPE.Add(edgeTransform, positionEncoding)
// 传播到下一个节点,应用节点的偏置和激活函数
nodeInput := mat.NewDense(nextNode.embedding.Rows(), nextNode.embedding.Cols(), nil)
nodeInput.Add(signalWithPE, nextNode.bias)
// 应用GeLU激活函数
output := mat.NewDense(nodeInput.Rows(), nodeInput.Cols(), nil)
for i := 0; i < nodeInput.Rows(); i++ {
for j := 0; j < nodeInput.Cols(); j++ {
val := nodeInput.At(i, j)
if val > 0 {
output.Set(i, j, val)
} else {
output.Set(i, j, 0)
}
}
}
return output
}
信号能量计算
计算信号在节点处的能量:
// computeEnergy 计算信号的L2能量
func computeEnergy(signal \*mat.Dense) float64 {
// 计算L2范数的平方
sumSq := 0.0
for i := 0; i < signal.Rows(); i++ {
for j := 0; j < signal.Cols(); j++ {
val := signal.At(i, j)
sumSq += val \* val
}
}
return sumSq
}
预测函数
实现基于信号传播的预测:
// predictNextToken 根据当前信号传播状态预测下一个token
func predictNextToken(graph \*Graph, currentPath \[]int, maxSteps int, positionEncodings \[]\*mat.Dense) int {
currentSignal := mat.NewDense(32, 1, nil) // 假设节点维度是32
for i := 0; i < 32; i++ {
currentSignal.Set(i, 0, 1.0) // 初始信号为全1向量
}
for step := 0; step < maxSteps; step++ {
if step >= len(currentPath) {
break
}
currentNode := graph.nodes\[currentPath\[step]]
if step == len(currentPath)-1 {
// 最后一步,尝试所有可能的边
maxEnergy := -1.0
bestNextNode := -1
for \_, edge := range graph.edges {
if edge.from != currentNode.id {
continue
}
pe := positionEncodings\[step]
nextSignal := propagateSignal(currentSignal, edge, graph.nodes\[edge.to], pe)
energy := computeEnergy(nextSignal)
if energy > maxEnergy {
maxEnergy = energy
bestNextNode = edge.to
}
}
return bestNextNode
}
nextNodeID := currentPath\[step+1]
edgeKey := fmt.Sprintf("%d-%d", currentNode.id, nextNodeID)
edge := graph.edges\[edgeKey]
if edge == nil {
// 如果边不存在,随机选择一个可能的边
// 这里为了简化,假设所有节点之间都有边
// 实际实现中需要处理这种情况
return -1
}
pe := positionEncodings\[step]
currentSignal = propagateSignal(currentSignal, edge, graph.nodes\[nextNodeID], pe)
}
// 如果到达最大步数仍未找到,随机选择一个节点(实际应用中应避免这种情况)
return rand.Intn(len(graph.nodes))
}
模型初始化
初始化一个简化的 BriLLM 图结构:
func initializeGraph(vocabSize int, embeddingSize int) \*Graph {
graph := \&Graph{
nodes: make(\[]\*Node, vocabSize),
edges: make(map\[string]\*Edge),
}
// 初始化节点
for i := 0; i < vocabSize; i++ {
embedding := mat.NewDense(embeddingSize, 1, nil)
for j := 0; j < embeddingSize; j++ {
embedding.Set(j, 0, rand.NormFloat64())
}
bias := mat.NewDense(embeddingSize, 1, nil)
for j := 0; j < embeddingSize; j++ {
bias.Set(j, 0, rand.NormFloat64()\*0.1)
}
graph.nodes\[i] = \&Node{
id: i,
embedding: embedding,
bias: bias,
}
}
// 初始化边
for i := 0; i < vocabSize; i++ {
for j := 0; j < vocabSize; j++ {
if i == j {
continue // 不允许自环
}
weight := mat.NewDense(embeddingSize, embeddingSize, nil)
for k := 0; k < embeddingSize; k++ {
for l := 0; l < embeddingSize; l++ {
weight.Set(k, l, rand.NormFloat64()\*0.01)
}
}
edge := \&Edge{
from: i,
to: j,
weight: weight,
}
graph.edges\[fmt.Sprintf("%d-%d", i, j)] = edge
}
}
return graph
}
位置编码生成
实现位置编码:
// generatePositionEncodings 生成位置编码矩阵
func generatePositionEncodings(maxLen int, embeddingSize int) \[]\*mat.Dense {
pe := make(\[]\*mat.Dense, maxLen)
for pos := 0; pos < maxLen; pos++ {
p := mat.NewDense(embeddingSize, 1, nil)
for i := 0; i < embeddingSize; i++ {
if i%2 == 0 {
p.Set(i, 0, math.Sin(float64(pos)/math.Pow(10000, float64(i)/embeddingSize)))
} else {
p.Set(i, 0, math.Cos(float64(pos)/math.Pow(10000, float64(i-1)/embeddingSize)))
}
}
pe\[pos] = p
}
return pe
}
主函数示例
使用上述组件的主函数示例:
func main() {
vocabSize := 4000 // 假设词汇表大小为4000
embeddingSize := 32 // 节点维度为32
maxSequenceLength := 16 // 最大序列长度为16
// 初始化图
graph := initializeGraph(vocabSize, embeddingSize)
// 生成位置编码
positionEncodings := generatePositionEncodings(maxSequenceLength, embeddingSize)
// 示例输入序列(假设已经转换为节点ID列表)
inputSequence := \[]int{10, 20, 30} // 假设这是"hello world"的节点ID序列
// 预测下一个token
nextToken := predictNextToken(graph, inputSequence, maxSequenceLength, positionEncodings)
fmt.Printf("Predicted next token: %d\n", nextToken)
}
以上我们实现了BriLLM 的核心机制:信号在图结构中的传播,以及基于能量最大化的预测。
但请注意,实际应用中需要考虑更多细节,如训练过程、稀疏边处理、信号整合等,但这个简化版本足以展示其基本工作原理。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号