CF1491D. Zookeeper and The Infinite Zoo

CF1491D. Zookeeper and The Infinite Zoo

题目描述

There is a new attraction in Singapore Zoo: The Infinite Zoo.

The Infinite Zoo can be represented by a graph with an infinite number of vertices labeled $1,2,3,\ldots $. There is a directed edge from vertex \(u\) to vertex \(u+v\) if and only if \(u\&v=v\), where \(\&\) denotes the bitwise AND operation. There are no other edges in the graph.

Zookeeper has q queries. In the \(i\)-th query she will ask you if she can travel from vertex \(u_i\) to vertex \(v_i\) by going through directed edges.

题目大意

有无穷多个点，对于任意两点\(u\)，\(v + u\)，如果满足\(u\&v=v\)，那么即有一条由\(u\)到\(u+v\)的单向边。有\(q\)组询问，回答\(u_i\)能否到达\(v_i\)

解题思路

首先显而易见的,如果\(u_i < v_i\)那么显然无法到达。而在\(u_i = v_i\)的情况下，则不需要移动已经到达。

对于其余的情况，我们考虑在移动时\(u_i\)每一位的变化情况。
观察\(u_i\)到\(v_i\)时二进制下每一位上的变化情况，我们可以发现对于满足\(u\&v=v\)的\(v\)，它将\(u\)中同为\(1\)的位向右移了一位。
如图例所示，\(v\)将\(u\)中的第\(1\)和第\(3\)位分别移动到了第\(2\),\(4\)位。

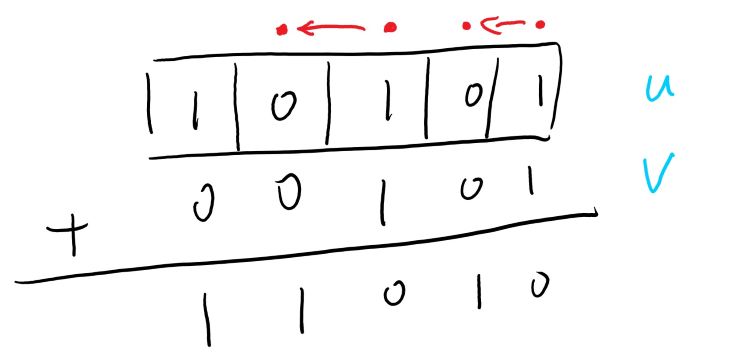
所以我们可以得出一个小结论，对于\(v_i\)中每一位的\(1\)，在其右侧都有\(u_i\)中的一个或多个(多个\(1\)被移动到了同一位上)与之对应。

然后就可以愉快地写出代码

代码

#include<bits/stdc++.h>
using namespace std;
const int maxbit = 30;
void solve() {
	int u, v;
	cin >> u >> v;
	if (v < u) {
		cout << "NO\n";
		return;
	}
	int cnt = 0;
	for (int i = 0; i <= 30; i++) {
		int x = (u >> i) & 1;
		int y = (v >> i) & 1;
		if (x)
			cnt++;
		if (y)
			cnt--;
		if (cnt < 0) {
			cout << "NO\n";
			return;
		}
	}
	cout << "YES\n";
	return;
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int t;
	cin >> t;
	while(t--)
		solve();
	return 0;
}