贝塞尔曲线

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋。

贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

贝塞尔曲线原理

贝塞尔曲线由n个点来决定，其曲线轨迹可以由一个公式来得出：

\[B(t) = \sum_{i=0}^{n}\binom{n}{i}P_i(1-t)^{n-i}t^i=\binom{n}{0}P_0(1-t)^nt^0+\binom{n}{1}P_1(1-t)^{n-1}t^1+...+\binom{n}{n-1}P_{n-1}(1-t)^1t^{n-1}+\binom{n}{n}P_n(1-t)^0t^n,t\in [0,1] \]

其中n就代表了贝塞尔曲线是几阶曲线，该公式描述了曲线运动的路径。

以下我们来讨论一下，贝塞尔公式如何推导。

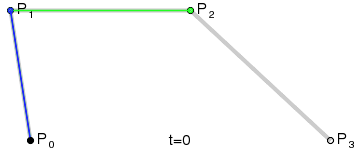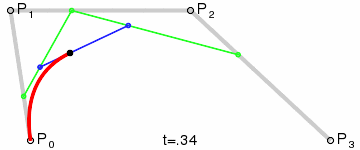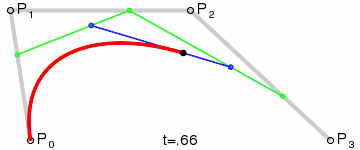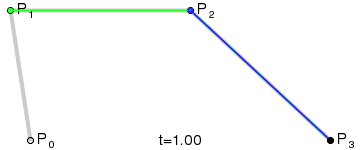
一阶贝塞尔曲线

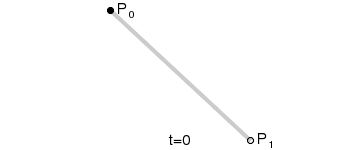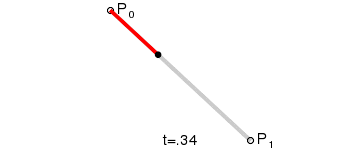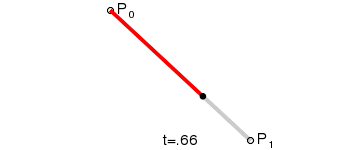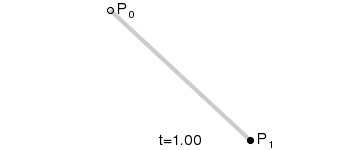
设定图中运动的点为\(P_t\)，\(t\)为运动时间，\(t∈(0,1)\)，可得如下公式

\[P_t=P_0+(P_1-P_0)t=(1-t)P_0+tP_1 \]

二阶贝塞尔曲线

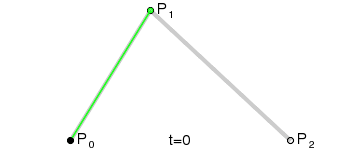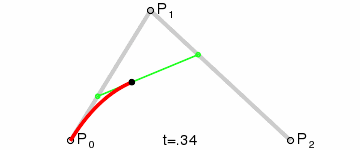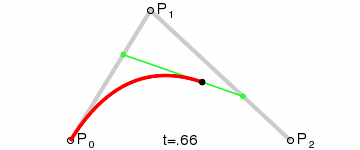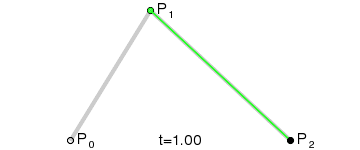
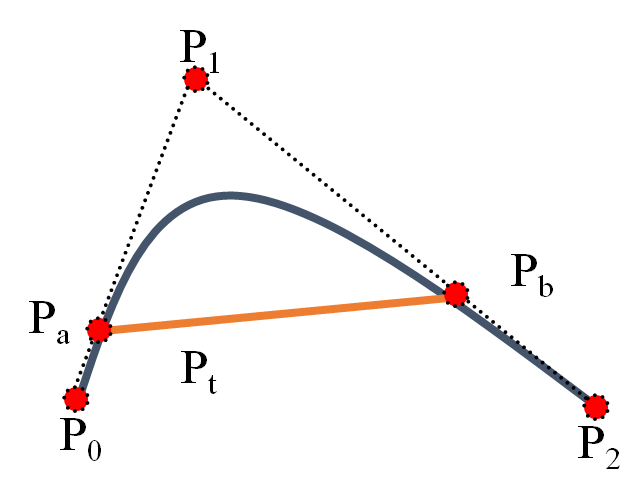
在二阶贝塞尔曲线中，已知三点恒定\((P_0,P_1,P_2)\)，设定在\(P_0P_1\)中的点为\(P_a\)，在\(P_1P_2\)中的点为\(P_b\)，\(P_t\)在\(P_aP_b\)上的点，这三点都在相同时间t内做匀速运动。

由公式(2)可知：

\[P_a=P_0+(P_1-P_0)t=(1-t)P_0+tP_1 \]

\[P_b=P_1+(P_2-P_1)t=(1-t)P_1+tP_2 \]

\[P_t=P_a+(P_b-P_a)t=(1-t)P_a+tP_b \]

将公式(3)(4)代入公式(5)中，可得：

\[\begin{aligned} P_t&=(1-t)P_a+tP_b\\ &=(1-t)[(1-t)P_0+tP_1]+t[(1-t)P_1+tP_2]\\ &= (1-t)^2P_0+2(1-t)tP_1+t^2P_2\qquad(6) \end{aligned} \]

三阶贝塞尔曲线

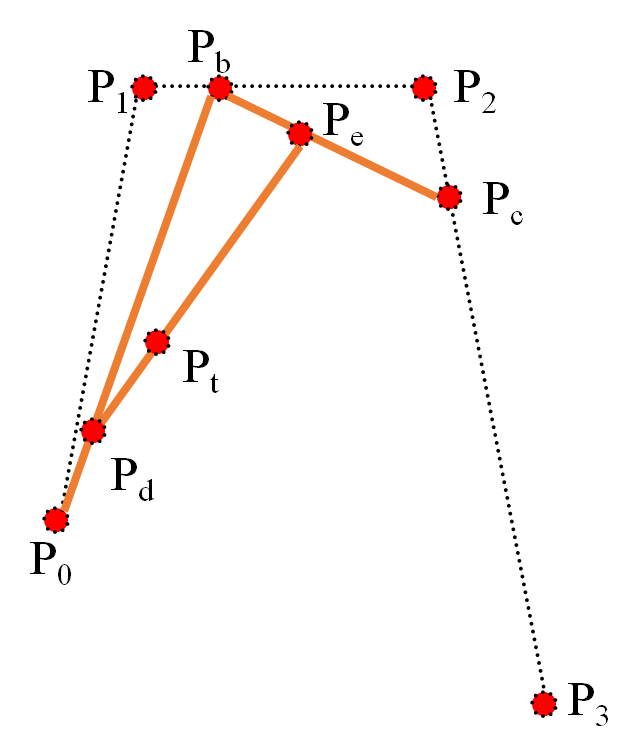
同理，根据以上的推导过程可得

\[P_a=P_0+(P_1-P_0)t=(1-t)P_0+tP_1\\ P_b=P_1+(P_2-P_1)t=(1-t)P_1+tP_2\\ P_c=P_0+(P_2-P_3)t=(1-t)P_2+tP_3\\ P_d=P_a+(P_b-P_a)t=(1-t)P_a+tP_b\\ P_e=P_b+(P_c-P_b)t=(1-t)P_b+tP_c\\ \]

由此可以推导

\[P_t=P_d+(P_c-P_d)t=...=(1-t)^3P_0+3t(1-t)^2tP_1+3t^2(1-t)P_2+t^3P_3\quad t\in(0,1) \]

n阶贝塞尔曲线

设\(n+1\)个控制点\(P_0,P_1…P_n\)，其中\(P_k=(X_k,Y_k,Z_k), 0≤k≤n\)

n次Bezier曲线为：

\[P(t) = \sum P_iB_{i,n}(t), 0\le t \le 1 \]

其中， \(B_in(t)\)是Bernstern基函数，即

\[B_{i,n}(t)=C_n^it^i(1-t)^{n-i}\\ \]

\[C_n^i=\frac{n!}{i!(n-i)!}\quad i=0,1,2,...,n \]

曲线在两个端点处的边界条件

起点是第一个控制点，终点是最后一个控制点

\(P(0)=P_0,P(1)=P_n\)

证明

\[\begin{align*} &P(0)= \sum P_iB_{i,n}(t)= \sum P_iB_{i,n}(0)\\ &B_{i,n}(0)=C_n^it^i(1-t)^{n-i}=C_n^i0^i\\ &i=0时0^0=1\\ &B_{0,n}(0)=C_n^0=1\\ &B_{i,n}(0)=0\qquad(i\neq 0{时})\\ &\therefore P(0)=P_0 \end{align*} \]

\[\begin{align*} &P(1)= \sum P_iB_{i,n}(1)\\ &B_{i,n}(1)= C_n^i1^i(1-1)^{n-i}\\ &B_{n,n}(1)=C_n^n1^n0^0=1\qquad(i=n时)\\ &B_{i,n}(1)=0\qquad (i\neq n时)\\ &\therefore P(1)=P_n \end{align*} \]

其他

Bezier曲线在端点处的一阶导数值可以由控制点坐标计算：

\[P’(0)=-nP_0+nP_1\\ P’(1)=-nP_n-1+nP_n \]

曲线起点的切线在头两个控制点连线上。

曲线终点的切线在最后两个控制点连线上。

Bezier曲线落在控制点的凸包内（凸多边形边界）

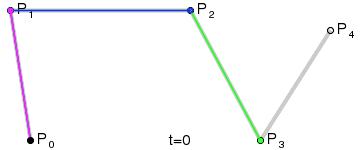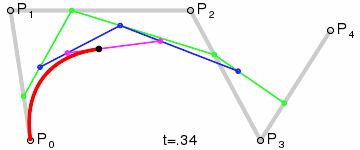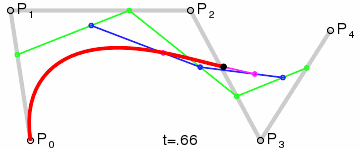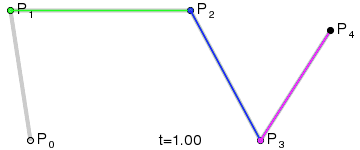
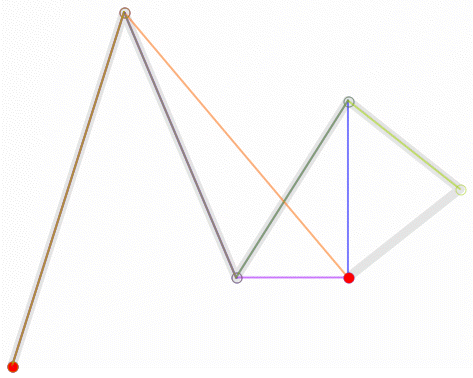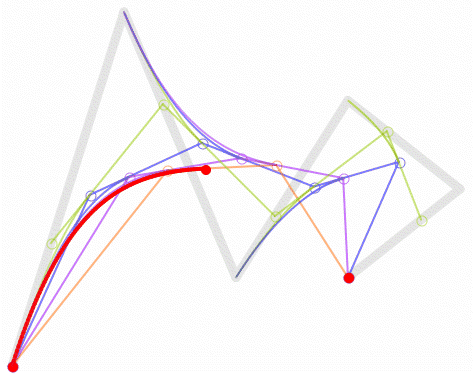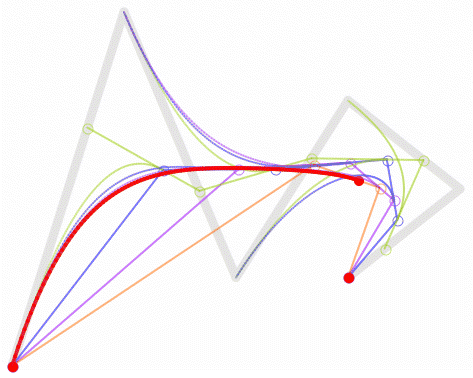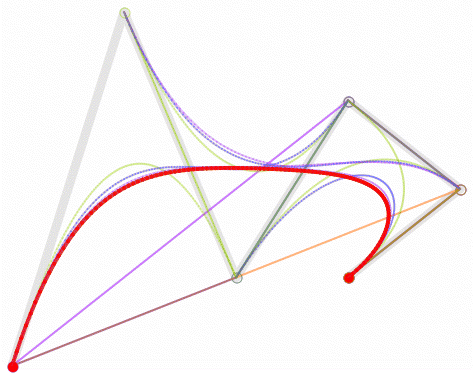
Bezier曲线的Casteljau算法

详细算法可看：https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html

前提：三切线定理

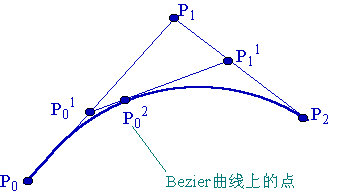
设\(P_0\)、\(P_0^2\)、\(P_2\)是一条抛物线上顺序三个不同的点。过\(P_0\)和\(P_2\)点的两切线交于\(P_1\)点，在\(P_0^2\)点的切线交\(P_0P_1\)和\(P_2P_1\)于\(P_0^1\)和\(P_1^1\)，则如下比例成立：

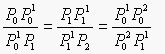
这是所谓抛物线的三切线定理。

证明

当\(P_0\)，\(P_2\)固定，引入参数\(t\)，令上述比值为\(\frac {t}{1-t}\)，即有：

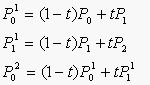
\(t\)从\(0\)变到\(1\)，第一、二式就分别表示控制二边形的第一、二条边，它们是两条一次Bezier曲线。将一、.二式代入第三式得：

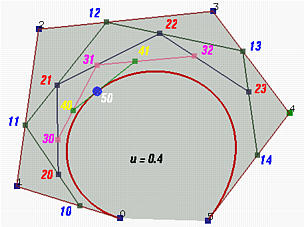
当\(t\)从\(0\)变到\(1\)时，它表示了由三顶点\(P_0\)、\(P_1\)、\(P_2\)三点定义的一条二次Bezier曲线。并且表明：这二次Bezier曲线\(P_0^2\)可以定义为分别由前两个顶点\((P_0,P_1)\)和后两个顶点\((P_1,P_2)\)决定的一次Bezier曲线的线性组合。依次类推，由四个控制点定义的三次Bezier曲线\(P_0^3\)可被定义为分别由\((P_0,P_1,P_2)\)和\((P_1,P_2,P_3)\)确定的2条二次Bezier曲线的线性组合，由\((n+1)\)个控制点\(P_i(i=0,1,...,n)\)定义的n次Bezier曲线\(P_0^n\)可被定义为分别由前、后\(n\)个控制点定义的两条\((n-1)\)次Bezier曲线\(P_0^{n-1}\)与\(P_1^{n-1}\)的线性组合：

\[P_0^n=(1-t)P_0^{n-1}+tP_1^{n-1}\qquad t\in [0,1] \]

由此得到Bezier曲线的递推计算公式，也就是de Casteljau算法：

\[P_i^k= \left\{\begin{matrix} P_i & k=0\\ (1-t)P_i^{k-1}+tP_{i+1}^{k-1} & k=1,2,...,n,i=0,1,...,n-k \end{matrix}\right. \]

代码示例

import numpy as np
import matplotlib.pyplot as plt
import bezier
b_xs = []
b_ys = []


# xs表示原始数据
# n表示阶数
# k表示索引
def one_bezier_curve(a, b, t):
    return (1 - t) * a + t * b


def n_bezier_curve(xs, n, k, t):
    if n == 1:
        return one_bezier_curve(xs[k], xs[k + 1], t)
    else:
        return (1 - t) * n_bezier_curve(xs, n - 1, k, t) + t * n_bezier_curve(xs, n - 1, k + 1, t)


def bezier_curve(xs, ys, num, b_xs, b_ys):
    n = 5  # 采用5次bezier曲线拟合
    t_step = 1.0 / (num - 1)
    # t_step = 1.0 / num
    print(t_step)
    t = np.arange(0.0, 1 + t_step, t_step)
    print(len(t))
    for each in t:
        b_xs.append(n_bezier_curve(xs, n, 0, each))
        b_ys.append(n_bezier_curve(ys, n, 0, each))


def func():
    xs = [1.0, 2.1, 3.0, 4.0, 5.0, 6.0]
    ys = [0, 1.1, 2.1, 1.0, 0.2, 0]
    num = 20

    bezier_curve(xs, ys, num, b_xs, b_ys)  # 将计算结果加入到列表中
    print(b_xs, b_ys)
    plt.figure()
    plt.plot(b_xs, b_ys, 'r')  # bezier曲线
    # plt.plot(xs, ys)  # 原曲线
    # plt.show()

func()