【强化学习的数学原理】课程笔记(一)——基本概念
说明:本内容为个人自用学习笔记,整理自b站西湖大学赵世钰老师的【强化学习的数学原理】课程,特别感谢老师分享讲解如此清楚的课程。
1. 引言

前两本书偏文字性介绍,后两本具有较强的数学性,较为难懂!
监督学习、无监督学习主要用来做分类、回归,强化学习关注于决策
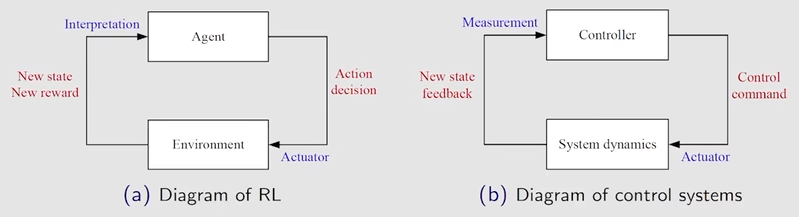
2. 基本概念
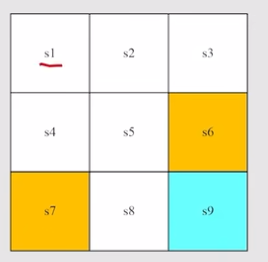
State: The status of agent with respect to the environment. In this example, there are nine possible states.
States space: the set of all states S = { s i } i = 1 9 S = \{s_i\}_{i=1}^{9} S={si}i=19
Action: 在每个state可以采取的行动,这里每个状态有5个Action
Action space of a state: 每个状态可能采取行动的集合, A ( s i ) = { a i } \mathcal{A}(s_i)=\{a_i\} A(si)={ai}
State transition: 状态转移 s 1 ⟶ a 2 s 2 s_1 \overset{a_2}{\longrightarrow} s_2 s1⟶a2s2
Forbidden area: is accessible but with penalty or is inaccessible
Tabular representation: 表格形式表达状态转移,只能表达确定性情况
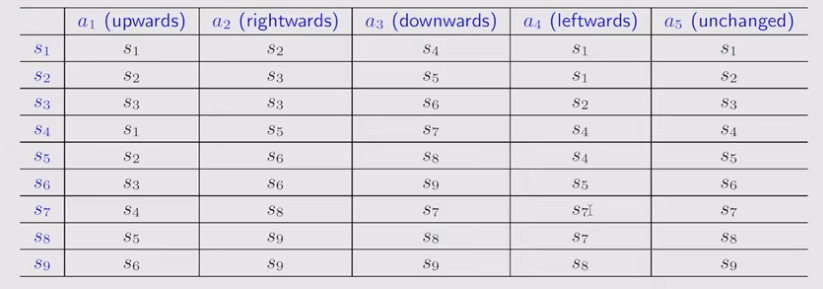
State transition probability: 用条件概率表达状态转移 p ( s 2 ∣ s 1 , a 2 ) = 1 p(s_2|s_1,a_2)=1 p(s2∣s1,a2)=1,既可以描述确定性情况,也可以描述随机转移。
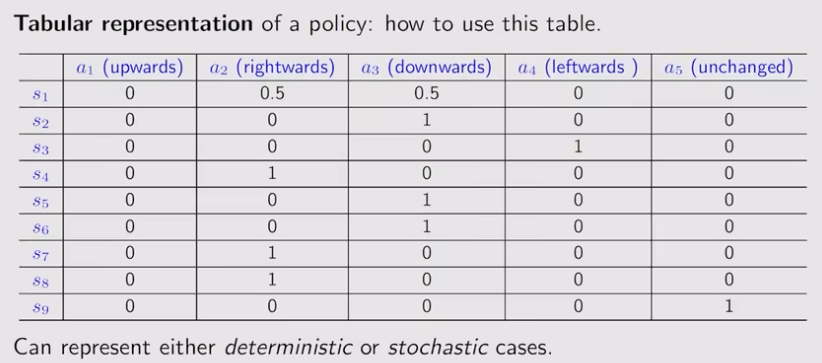
Policy: tell the agent what actions to take at a state, 直观表示可以用箭头描述,数学表达使用条件概率, π ( a 1 ∣ s 1 ) = 0 , π ( a 2 ∣ s 2 ) = 1 \pi(a_1|s_1) = 0,\quad \pi(a_2|s_2)=1 π(a1∣s1)=0,π(a2∣s2)=1,同样可以表示非确定性情况。表格表现如下,
Reward: get a scalar when agent take an action。正数代表鼓励,负数代表惩罚。 0代表无判定,一定程度上代表鼓励。
-
can be interpreted as a human-machine interface, with which we can guide the agent to behave as what we expect.
-
表格表示
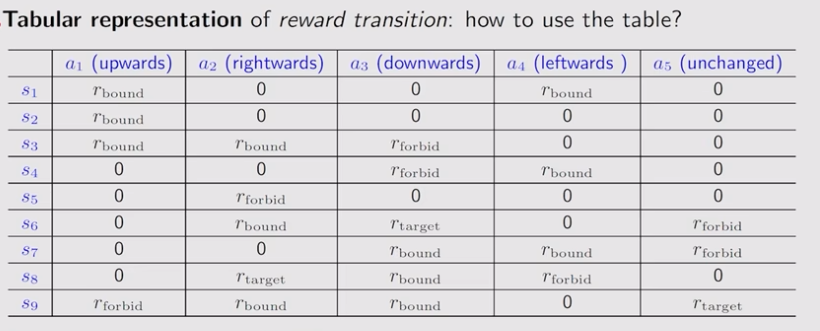
-
条件概率表示 p ( r = 1 ∣ s 1 , a 1 ) = 1 p(r=1|s_1, a_1) = 1 p(r=1∣s1,a1)=1
-
依赖于当前的state和action,而不是下一个状态。比如在 s 1 s_1 s1 采取 a 1 和 a 5 a_1 \text{和} a_5 a1和a5 这两个不同的action,但是下一状态都是 s 1 s_1 s1,但获得的收益是不一样的, a 1 a_1 a1 试图触碰边界,给予惩罚, a 5 a_5 a5 原地停留,不给予惩罚。
Trajectory: is a state-action -reward chain, s 1 → r = 0 a 2 s 2 → r = 0 a 3 s 5 → r = 0 a 3 s 8 → r = 1 a 2 s 9 s_1 \xrightarrow[r=0]{a_2} s_2\xrightarrow[r=0]{a_3} s_5 \xrightarrow[r=0]{a_3} s_8 \xrightarrow[r=1]{a_2} s_9 s1a2r=0s2a3r=0s5a3r=0s8a2r=1s9
Return: The return of this trajectory is the sum of all the rewards collected along the trajectory: r e t u r n = 0 + 0 + 0 + 1 = 1 return = 0+0+0+1 =1 return=0+0+0+1=1
Discounted return:
- discount rate: γ ∈ [ 0 , 1 ) \gamma \in \left[0,1 \right) γ∈[0,1)
- discounted return: r e t u r n = 0 + γ 0 + γ 2 0 + γ 3 1 = γ 3 return = 0+\gamma 0+\gamma^2 0+\gamma^3 1 =\gamma^3 return=0+γ0+γ20+γ31=γ3
- γ \gamma γ 接近0时,return 取决于最初获得的收益,将会更加关注近期reward, γ \gamma γ 接近1时,return 取决于累计收益,将会更加关注长远reward。
Episode: when interacting with the environment following a policy, the agent may stop at some terminal states. The resulting trajectory is called an episode(or a trail) .
continuing tasks: no terminal states
采取措施将 continuing tasks 转换为 episodic tasks,方式1,进入目标状态之后不再离开,将rewards 设置为0;方式2,将目标态当作一般状态处理,采取可能的策略还可以离开。本课程采用方式2处理。
3. MDP
3.1 MDP的关键要素
-
集合 Sets
- State: the set of state S \mathcal{S} S
- Action: the set of actions A ( s ) \mathcal{A}(s) A(s) is associated for state s ∈ S s \in \mathcal{S} s∈S
- Reward: the set of reward R ( s , a ) \mathcal{R}(s, a) R(s,a)
-
概率分布 Probability distribution
- state transition probability: at state s, taking action a, the probability to transit to state s’ is p ( s ′ ∣ s , a ) p(s'|s, a) p(s′∣s,a)
- Reward probability: at state s, taking action a, the probability to get reward r is p ( r ∣ s , a ) p(r|s,a) p(r∣s,a)
-
策略 policy—— at state s, the probability to choose action a is π ( a ∣ s ) \pi(a|s) π(a∣s)
-
Markov property—— memoryless property
p ( s t + 1 ∣ a t + 1 , s t , ⋯ , a 1 , s 0 ) = p ( s t + 1 ∣ a t + 1 , s t ) p ( r t + 1 ∣ a t + 1 , s t , ⋯ , a 1 , s 0 ) = p ( r t + 1 ∣ a t + 1 , s t ) p(s_{t+1}|a_{t+1},s_t,\cdots,a_1,s_0) = p(s_{t+1}|a_{t+1},s_{t}) \\ p(r_{t+1}|a_{t+1},s_t,\cdots,a_1,s_0) = p(r_{t+1}|a_{t+1},s_{t}) p(st+1∣at+1,st,⋯,a1,s0)=p(st+1∣at+1,st)p(rt+1∣at+1,st,⋯,a1,s0)=p(rt+1∣at+1,st)
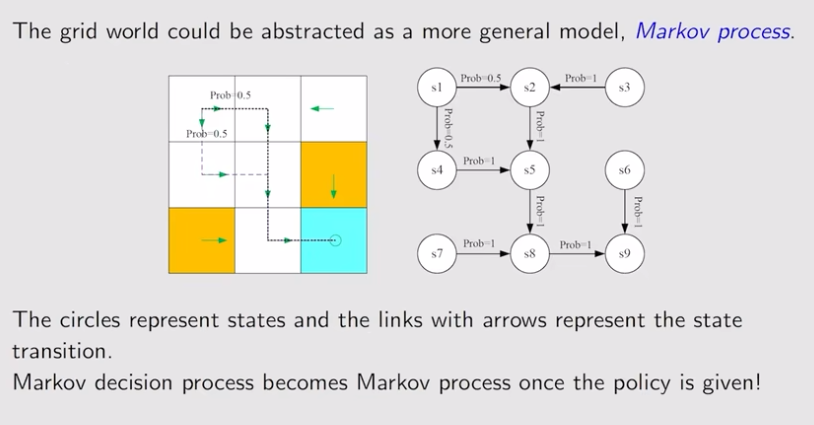
3.2 举例




 浙公网安备 33010602011771号
浙公网安备 33010602011771号