20172302 《Java软件结构与数据结构》第八周学习总结
2018年学习总结博客总目录:[第一周](https://www.cnblogs.com/hzy0628/p/9606767.html) [第二周](https://www.cnblogs.com/hzy0628/p/9655903.html) [第三周](https://www.cnblogs.com/hzy0628/p/9700082.html) [第四周](https://www.cnblogs.com/hzy0628/p/9737321.html) [第五周](https://www.cnblogs.com/hzy0628/p/9786586.html) [第六周](https://www.cnblogs.com/hzy0628/p/9825081.html) [第七周](https://www.cnblogs.com/hzy0628/p/9873230.html) [第八周](https://www.cnblogs.com/hzy0628/p/9929202.html)
教材学习内容总结
第十二章 优先队列与堆
1.堆(heap)是具有两个附加属性的一棵二叉树:
(1)它是一棵完全二叉树,即该树是平衡的,且底层所有叶子都位于树的左边。
(2)最小堆:对每一结点,它小于或等于其左孩子和右孩子。
最大堆:对每一结点,它大于或等于其左孩子和右孩子。
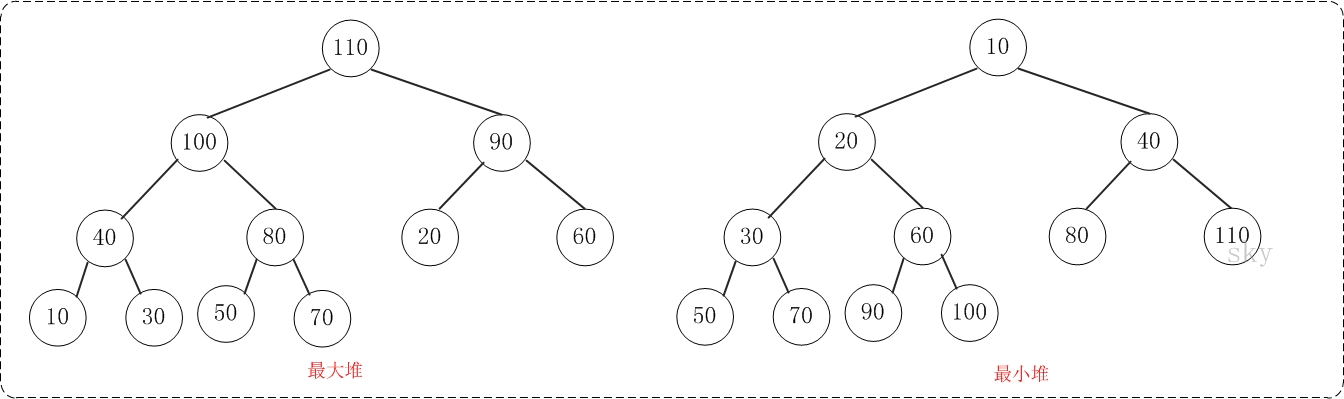
- 接下来所讨论内容是关于最小堆的。
2.堆的接口定义及其方法实现:
(1)addElement:将给定元素添加到该堆中;
对于新插入的结点而言,它只存在一个正确位置,且它要么是h层左边的下一个空位置,要么是h+1层左边的第一个位置(如果h层是满的的话)
(2)removeMin:删除堆的最小元素;
删除掉根结点,要找一个元素来替代它,则要维持树的完整性,那么只有一个能替换根的合法元素,且它是存储在树中最末一片叶子上的元素。
(3)findMin:返回一个指向堆中最小元素的引用。
返回存储在根处的元素即可。
3.使用堆:优先级队列
优先级队列:(1)具有更高优先级的项目在先(2)具有相同优先级的项目采用先进先出的方法来确定其排序。
4.用链表实现堆
-
(1)HeapNode类
继承自BinaryTreeNode类,在其基础上添加父结点及其set方法。 -
(2)addElement操作
①要添加一个元素,首先有最后一个结点的引用,要去得到新的最后一个结点的父结点
②然后将元素添加至最后结点,并更新最后结点的引用
③从新的最后结点处往上进行重排序,以保持其排序属性 -
(3)removeMin操作
①用存储在最末结点处的元素替换存储在根处的元素(这一步相当于已经把最小元素删除)
②将最末结点处的元素删除,即将最末结点处的父结点的左孩子或右孩子设为空
③更新最后结点的引用指向
④对堆进行重排序,从根开始,往下进行 -
findMin操作
返回一个指向存储在堆根处元素的引用
5.用数组实现堆
在二叉树的数组实现中,树的根位于位置0处,对于每一结点n,n的左孩子将位于数组的2n+1位置处,n的右孩子将位于数组的2(n+1)位置处。
- (1)addElement操作
①在恰当位置处添加新结点
②对堆进行重排序以维持其排序属性
③将count值递增1 - (2)removeMin操作
①用存储在最末元素处的元素替换存储在根处的元素
②对堆进行重排序,返回初始的根元素
③将原来的最末元素设为null,并将count值减1 - (3)findMin操作
返回数组的0位置处的元素
6.使用堆:堆排序
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
-
使用:将列表中的每个元素添加进堆里,然后一次删除一个元素
-
复杂度分析:对于任一给定的结点,插入到堆的复杂度都是O(logn),因此n个结点的插入复杂度将是O(nlogn),而对于删除一个结点的复杂度也是O(logn),因此对n个结点的删除也将会是O(nlogn)。对于堆排序算法,我们要执行addElement操作和removeMin操作各n次,因此最终的复杂度将是2×n×logn,即O(nlogn)。
教材学习中的问题和解决过程
-
问题1:一个疑问,之前学习栈的时候,经常会提到堆栈这个概念,那么堆、堆栈、栈分别是什么,区别与联系?
-
问题1解决方案:查找资料,我才发现,堆、栈、堆栈它们在这里不是指数据结构,而是Java中的存储结构。
在JAVA中,有六个不同的地方可以存储数据:
- 寄存器(register)。这是最快的存储区,因为它位于不同于其他存储区的地方——处理器内部。但是寄存器的数量极其有限,所以寄存器由编译器根据需求进行分配。你不能直接控制,也不能在程序中感觉到寄存器存在的任何迹象。
- 堆栈(stack)。位于通用RAM中,但通过它的“堆栈指针”可以从处理器哪里获得支持。堆栈指针若向下移动,则分配新的内存;若向上移动,则释放那些内存。这是一种快速有效的分配存储方法,仅次于寄存器。创建程序时候,JAVA编译器必须知道存储在堆栈内所有数据的确切大小和生命周期,因为它必须生成相应的代码,以便上下移动堆栈指针。这一约束限制了程序的灵活性,所以虽然某些JAVA数据存储在堆栈中——特别是对象引用,但是JAVA对象不存储其中。
- 堆(heap)。一种通用性的内存池(也存在于RAM中),用于存放所以的JAVA对象。堆不同于堆栈的好处是:编译器不需要知道要从堆里分配多少存储区域,也不必知道存储的数据在堆里存活多长时间。因此,在堆里分配存储有很大的灵活性。当你需要创建一个对象的时候,只需要new写一行简单的代码,当执行这行代码时,会自动在堆里进行存储分配。当然,为这种灵活性必须要付出相应的代码。用堆进行存储分配比用堆栈进行存储存储需要更多的时间。
- 静态存储(static storage)。这里的“静态”是指“在固定的位置”。静态存储里存放程序运行时一直存在的数据。你可用关键字static来标识一个对象的特定元素是静态的,但JAVA对象本身从来不会存放在静态存储空间里。
- 常量存储(constant storage)。常量值通常直接存放在程序代码内部,这样做是安全的,因为它们永远不会被改变。有时,在嵌入式系统中,常量本身会和其他部分分割离开,所以在这种情况下,可以选择将其放在ROM中
- 非RAM存储。如果数据完全存活于程序之外,那么它可以不受程序的任何控制,在程序没有运行时也可以存在。
就速度来说,有如下关系: 寄存器 < 堆栈 < 堆 < 其他
(1)new 的对象是存储在堆中的:
String s1 = "china";
String s2 = "china";
String s3 = "china";
String ss1 = new String("china");
String ss2 = new String("china");
String ss3 = new String("china");

(2)对于基础类型的变量和常量:变量和引用存储在栈中,常量存储在常量池中。
int i1 = 9;
int i2 = 9;
int i3 = 9;
public static final int INT1 = 9;
public static final int INT2 = 9;
public static final int INT3 = 9;
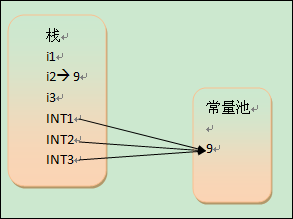
(3)堆栈:JVM 中的堆栈
JVM是基于堆栈的虚拟机.JVM为每个新创建的线程都分配一个堆栈.也就是说,对于一个Java程序来说,它的运行就是通过对堆栈的操作来完成的。堆栈以帧为单位保存线程的状态。JVM对堆栈只进行两种操作:以帧为单位的压栈和出栈操作。
代码调试中的问题和解决过程
-
问题1:在做PP12.1时,我使用的是ArrayHeap这个数组实现的堆来构造队列,但在删除一个元素之后元素个数没有变化

-
问题1解决方案:先看了一遍自己写的HeapQueue类没有问题后,就从书上ArrayHeap类找问题,
public T removeMin() throws EmptyCollectionException
{
if (isEmpty())
throw new EmptyCollectionException("ArrayHeap");
T minElement = tree[0];
tree[0] = tree[count-1];
heapifyRemove();
count--;
modCount--;
return minElement;
}
这是书上的代码,它在把堆的最后一个元素挪至第一位置后,并对进行重排序后,没有把这个最后一个元素给删掉,因此导致了这个问题,于是在这段代码之后加上tree[count] =null;即可解决问题。
那天写着光记着改了书上的错误了,没有把队列这个类的方法全部实现,后面经谭鑫提醒,才发现自己toString方法还没有修改,只是super.toString()了。在实现toString时,应该把这个最小堆按照层序输出就可以了,但是这样还是存在一个就是,一旦有一个元素出队了,那么再去用层序输出就不会是它本队列该有的顺序了。于是,有一个想法就是把toString方法改写为把每一个元素出队再入队这样输出出来,这样可能在时间复杂度上会变得比较高,但还没想到更好的解决办法。
public String toString()
{
String result = "";
int x = size();
for(int i=0;i<x;i++)
{
T t = dequeue();
result += t+" ";
enqueue(t);
}
return result;
}
代码托管

上周代码行数为13751行,现在为15816行,本周2065行。
上周考试错题总结
-
错题1.A minheap stores its largest element at the root of the binary tree, and both children of the root of a minheap are also minheaps.(×)
-
解析:一个最小堆在其根结点存储的是其最小元素,同时它的两个孩子也是最小堆。做题时没有认真看清楚,只关注了后半部分,导致错误。
-
错题2:Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.(×)
-
解析:又是只关注了后半部分,前半部分的说法是错误的,堆不是一个二叉搜索树,而是一个二叉平衡树。
-
错题3:One of the uses of trees is to provide simpler implementations of other collections.(×)
-
解析:树的主要应用之一是为其他集合提供高效的实现,而非简单的实现。简单≠高效。
结对及互评
- 本周结对学习情况
- 20172308
- 博客中值得学习的或问题:本周结对伙伴博客内容非常充实,教材内容总结面面俱到,教材中的问题总结也很详细,完整记录了查找资料和学习的过程。
- 结对学习内容:第十二章——堆
其他(感悟、思考等)
感悟
- 本周堆这一章内容是先听老师讲了一遍,然后才课下学,这一章书上的内容学起来难度不算大,主要的时间都花在了实验上。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 15/15 | |
| 第二周 | 572/572 | 1/2 | 16/31 | |
| 第三周 | 612/1184 | 1/3 | 13/44 | |
| 第四周 | 1468/2652 | 2/5 | 13/57 | |
| 第五周 | 1077/3729 | 1/6 | 14/71 | 初步理解各个排序算法 |
| 第六周 | 1087/4816 | 1/7 | 17/88 | 认识树结构 |
| 第七周 | 1252/6068 | 1/8 | 19/107 | 平衡二叉树、AVL树、红黑树 |
| 第八周 | 2065/8133 | 2/10 | 17/124 | 堆、最小堆 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号