20172302 《Java软件结构与数据结构》实验三:查找与排序实验报告
课程:《Java软件结构与数据结构》
班级: 1723
姓名: 侯泽洋
学号:20172302
实验教师:王志强老师
实验日期:2018年11月19日
必修/选修: 必修
实验内容
-
(1)定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169),最后完成测试。要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位提交运行结果图。
-
(2)重构你的代码,把Sorting.java Searching.java放入 cn.edu.besti.cs1723.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1723.G2301),把测试代码放test包中,重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
-
(3)参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试,提交运行结果截图
-
(4)补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)测试实现的算法(正常,异常,边界)提交运行结果截图
-
(5)编写Android程序对各种查找与排序算法进行测试,提交运行结果截图,推送代码到码云
实验过程及结果
(1)实验一
定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169)
SelectionSort方法测试:
测试正常情况:
@Test
public void testNormal() throws Exception
{
Integer[] integers1 = {2,7,12,13,14,23,29,32,46,56};
Integer[] integers2 = {7,32,12,46,14,56,29,13,23,2};
Sorting.selectionSort(integers2);
for (int i=0;i<integers2.length;i++)
assertEquals(integers1[i],integers2[i]);
}
测试异常情况:
@Test
public void testAbnormal() throws Exception
{
Integer[] integers1 = {2,7,12,13,14,23,29,32,46,56};
Integer[] integers2 = {7,32,12,46,14,56,29,14,23,2};
Sorting.selectionSort(integers2);
boolean result1 = true;
for (int i =0 ;i<integers2.length;i++)
{
if (integers1[i]!=integers2[i])
{
result1 = false;
break;
}
}
assertEquals(false,result1);
}
测试边界情况:
@Test
public void testBoundary () throws Exception{
Integer[] integers1 = {2,7,12,13,14,23,29,32,46,8961};
Integer[] integers2 = {7,32,12,46,14,8961,29,14,23,2};
Sorting.selectionSort(integers2);
boolean result1 = true;
for (int i =0 ;i<integers2.length;i++)
{
if (integers1[i]!=integers2[i])
{
result1 = false;
break;
}
}
assertEquals(false,result1);
}
测试逆序:
@Test
public void testReversed() throws Exception
{
Integer[] integers1 = {56,46,32,29,23,14,13,12,7,2};
Integer[] integers2 = {7,32,12,46,14,56,29,13,23,2};
Sorting.selectionSort(integers2);
for (int i=0;i<integers2.length;i++)
assertEquals(integers1[integers1.length-1-i],integers2[i]);
}
测试结果:
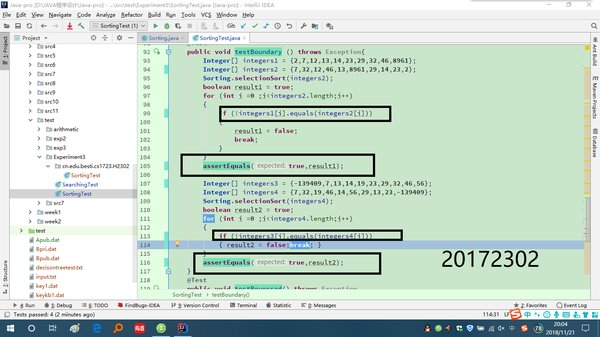

[测试用例代码]https://gitee.com/CS-IMIS-23/Java-pro/commit/6fff44510202eac172b3cbd26756c6554797802d
(2)实验二
- 重构代码,把Sorting.java Searching.java放入 cn.edu.besti.cs1723.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1723.G2301),把测试代码放test包中,重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
时间不够没有完成命令行,虚拟机也卸载掉了,只完成了第一种IDEA,对代码重构,放入指定包中。
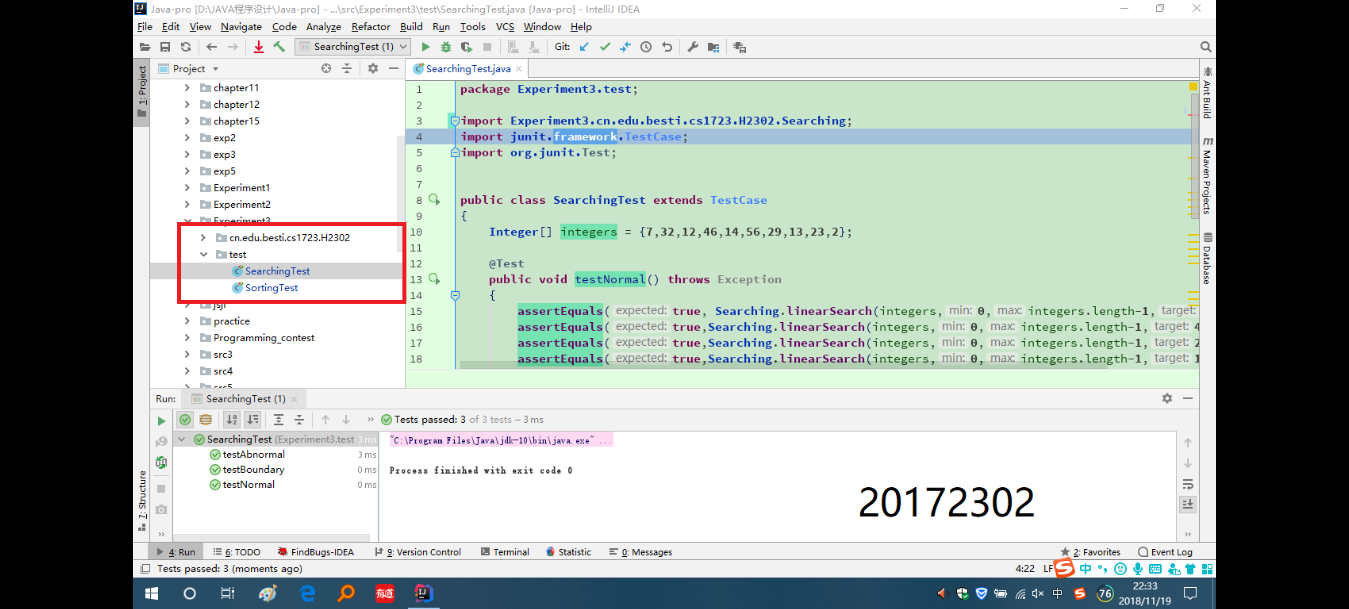
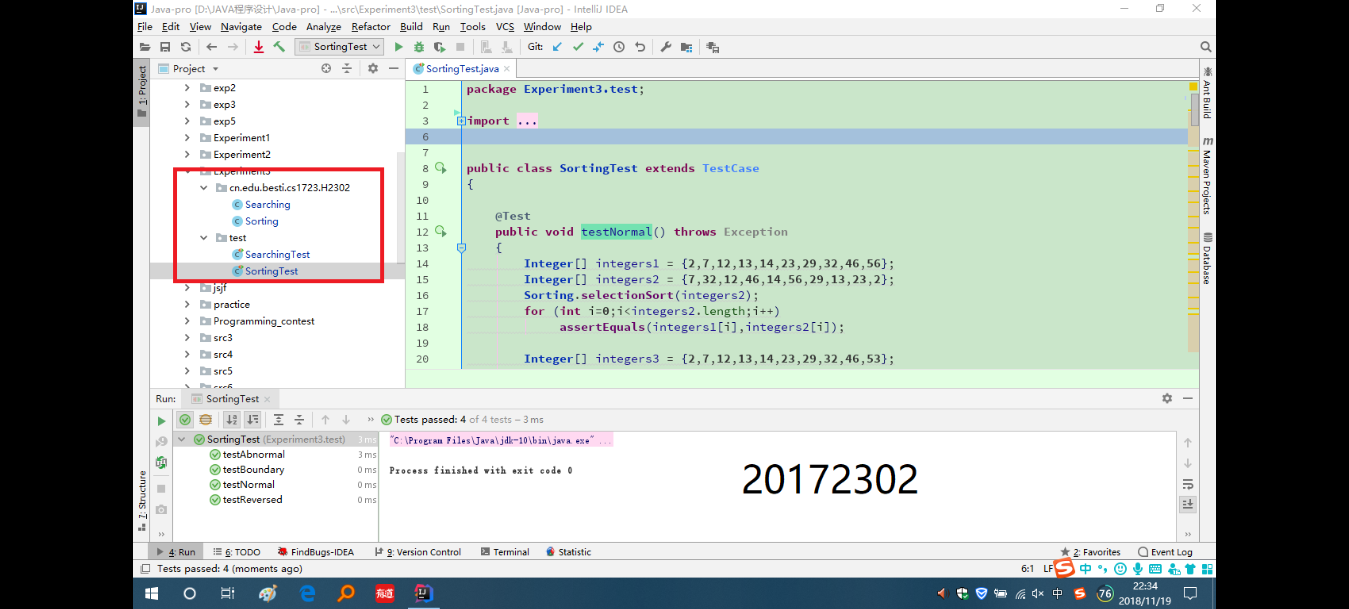
(3)实验三
参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试,提交运行结果截图
七种查找算法:线性查找、二分查找、插值查找、斐波那契查找、树表查找、分块查找、哈希查找
七种里面,斐波那契查找和分块查找是两个新学的,也比较有意思
斐波那契查找的原理是利用斐波那契数列的特性来进行查找的,不是以二分的比列来查找,而是按照黄金比列0.618来进行分割查找,这样做的好处是:
关于斐波那契查找, 如果要查找的记录在右侧,则左侧的数据都不用再判断了,不断反复进行下去,对处于当众的大部分数据,其工作效率要高一些。所以尽管斐波那契查找的时间复杂度也为O(logn),但就平均性能来说,斐波那契查找要优于折半查找。可惜如果是最坏的情况,比如这里key=1,那么始终都处于左侧在查找,则查找效率低于折半查找。
还有关键一点,折半查找是进行加法与除法运算的(mid=(low+high)/2),插值查找则进行更复杂的四则运算(mid = low + (high - low) * ((key - a[low]) / (a[high] - a[low]))),而斐波那契查找只进行最简单的加减法运算(mid = low + F[k-1] - 1),在海量数据的查找过程中,这种细微的差别可能会影响最终的效率。
代码实现:
/*构造一个斐波那契数组*/
public static void Fibonacci(int[] F)
{
F[0]=0;
F[1]=1;
for(int i=2;i<max_size;++i)
F[i]=F[i-1]+F[i-2];
}
//斐波那契查找
public static <T extends Comparable<? super T>>
boolean FibonacciSearch(T[] data, int min, int max, T target)
{
int length = max - min +1;
int[] F = new int[max_size];
Fibonacci(F);
int k=0;
while (length>(F[k]-1))
{
k++;
}
Object[] temp = new Object[max_size];
System.arraycopy(data,0,temp,0,data.length-1);
for (int i=length;i<F[k]-1;i++)
{
temp[i] = data[length-1];
}
while(min<=max)
{
int mid=min+F[k-1]-1;
if(target.compareTo((T) temp[mid])<0)
{
max=mid-1;
k-=1;
}
else if(target.compareTo((T)temp[mid])>0)
{
min=mid+1;
k-=2;
}
else
{
return true;
}
}
return false;
}
分块查找给我的第一感觉是快速排序算法,这进行划分,就用了原快速排序算法中的partition方法,我将整个数组分成了四块,进行了三次划分,然后根据比较结果确定元素所在区域,然后进行线性查找。
public static <T extends Comparable<? super T>>
boolean partitionSearch(T[] data, int min, int max, T target)
{
boolean result = false;
int partition1 = partition(data,min,max);
int partition2 = partition(data,min,partition1-1);
int partition3 = partition(data,partition1+1,max);
if (target.compareTo(data[partition1])==0)
return true;
else
{
if (target.compareTo(data[partition1])<0)
{
if (target.compareTo(data[partition2])==0)
return true;
else
{
if (target.compareTo(data[partition2])<0)
result = linearSearch(data,min,partition2-1,target);
else
result = linearSearch(data,partition2+1,partition1-1,target);
}
}
else
{
if (target.compareTo(data[partition3])==0)
return true;
else
{
if (target.compareTo(data[partition3])<0)
result = linearSearch(data,partition1+1,partition3-1,target);
else
result = linearSearch(data,partition3+1,max,target);
}
}
}
return result;
}
(4)实验四
补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等
希尔排序是新学的部分,一开始我对这里的希尔排序和之前做过的一个冒泡排序的升级的间隔排序法分辨不清,怎么也弄不明白这两个有什么区别,问题会记录这里。
将无序数组分割为若干个子序列,子序列不是逐段分割的,而是相隔特定的增量的子序列,对各个子序列进行插入排序;然后再选择一个更小的增量,再将数组分割为多个子序列进行排序......最后选择增量为1,即使用直接插入排序,使最终数组成为有序。
增量的选择:在每趟的排序过程都有一个增量,至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序);根据增量序列的选取其时间复杂度也会有变化,这个不少论文进行了研究,在此处就不再深究;本文采用首选增量为n/2,以此递推,每次增量为原先的1/2,直到增量为1;



实现代码:
public static <T extends Comparable<T>>void heapSort(T[] data)
{
LinkedHeap<T> linkedHeap = new LinkedHeap<>();
for (int i=0;i<data.length;i++)
linkedHeap.addElement(data[i]);
for (int i=0;i<data.length;i++)
data[i] = linkedHeap.removeMin();
}
实验代码非常简单。
(5)实验五
编写Android程序对各种查找与排序算法进行测试,提交运行结果截图,推送代码到码云
在Android上把这些算法都进行了测试,录了一个短的视频。
[链接]:https://www.mosoteach.cn/web/index.php?c=interaction_homework&m=homework_result_list&clazz_course_id=8CE1B708-B1CE-11E8-AA22-7CD30AD36C02&id=45E962C9-D25E-E6A1-697E-5820A8FAC84E
[代码链接]:https://gitee.com/CS-IMIS-23/Java-pro/commit/5b4d837f976592fbed90a14a3e7e194bc63997fd
实验过程中遇到的问题和解决过程
-
问题1:关于泛型数组如何实例化?直接这样
T[] temp = new T[];出现错误。

-
问题1解决方案:参照书上之前的代码进行实例化
T[] array;
array = (T[]) new Object[10];
还找到一种方法是数组就是Object类型,使用再将Object类型强制转化为T类型也是可以。
-
问题2:希尔排序和间隔排序法的一个区别?
-
问题2解决方案:
希尔排序是对间隔为一定距离的这些元素,全部进行排序,也就是说,经过这么一次排序之后,那么间隔为该距离的元素构成的一个集合一定是已排序好的。
而间隔排序做的是从最开始元素开始,对这些元素,把大的放在后面,一次排序后,间隔为该距离的元素构成的集合不一定有序。但最后面的那个一定是最大的。
举个简单的例子:
对 {9 7 6 4 3}进行排序
希尔排序第一轮
间隔为2进行,得到 3 4 6 7 9 即 3、6、9是有序的,4、7是有序的。
间隔排序第一轮
得到 6 4 3 7 9,即9放到了后面,7也被放到了后面。
这就产生了差别,两者在实现的代码上也有较大区别。
其他(感悟、思考等)
- 本次实验主要的是排序和查找的算法的一些设计,帮助我们复习了之前的内容,同时也为接下来的Android开发提供了一个方向。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号