Noip模拟12 2021.7.12

T1 interval

亏得昨天晚上改掉了T3并且理解了单调栈，今天一扫这题目就知道要用啥了。

先预处理出以a[i]为最大值的最大左右区间。然后再将a[i]取%！！！是的，要不然会影响单调栈的使用。。。

注意一下，这个题的前缀和与a[i]数组都要取%优化，类似《入阵曲》。

可以知道，一个合法的区间应满足。

 

 

然后就是昨天T3的类似启发式优化，找到距离较小的区间。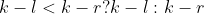

然后枚举那个区间里的每一个位置，都可以算出一个数（以下拿枚举左区间举例）：

 

 

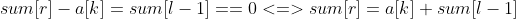
 等价右面的柿子就是我们枚举要求的。我们相当于求出一个sum[r]然后通过之前处理出的vector数组去右区间寻找等于sum[r]的数的个数（vector记录每个数（取%以后的）出现的位置）。运用便捷的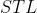——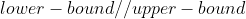即可实现。

最后是有一个小容斥，就是在计算区间时没有讨论l==r的情况，这种情况共n个，ans-n即可。

#include<bits/stdc++.h>
#define int long long
#define write(X) printf("%lld\n",X)
#define Min(A,B) ((A)<(B)?(A):(B))
#define Max(A,B) ((A)>(B)?(A):(B))
using namespace std;
inline int read(){
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}

const int NN=3e6+5000;
int n,K,a[NN],sum[NN],ll[NN],rr[NN],ans;
stack<int> s,t;
vector<int> g[NN];
void work(int k,int l,int r){
    if(k-l<r-k){
        for(int i=l;i<=k;i++){
            int tmp=(sum[i-1]+a[k])%K;
            int ans1=lower_bound(g[tmp].begin(),g[tmp].end(),k)-g[tmp].begin();
            int ans2=upper_bound(g[tmp].begin(),g[tmp].end(),r)-g[tmp].begin();
            ans+=ans2-ans1;
        }
    }
    else{
        for(int i=k;i<=r;i++){
            int tmp=(sum[i]-a[k]+K)%K;
            int ans1=lower_bound(g[tmp].begin(),g[tmp].end(),l-1)-g[tmp].begin();
            int ans2=upper_bound(g[tmp].begin(),g[tmp].end(),k-1)-g[tmp].begin();
            ans+=ans2-ans1;
        }
    }
}
namespace WSN{
    inline int main(){
        n=read(); K=read();
        g[0].push_back(0);
        for(int i=1;i<=n;i++){
            a[i]=read();
            sum[i]=(a[i]+sum[i-1])%K;
            g[sum[i]].push_back(i);
        }
        for(int i=1;i<=n;i++){
            while(!s.empty() && a[i]>a[s.top()]) s.pop();
            if(s.empty()) ll[i]=1;
            else ll[i]=s.top()+1;
            s.push(i);
        }
        for(int i=n;i;i--){
            while(!t.empty() && a[i]>=a[t.top()]) t.pop();
            if(t.empty()) rr[i]=n;
            else rr[i]=t.top()-1;
            t.push(i);
        }
        for(int i=1;i<=n;i++) a[i]%=K;
        for(int i=1;i<=n;i++) work(i,ll[i],rr[i]);
        write(ans-n);
        return 0;
    }
}
signed main(){return WSN::main();}

T2 random

可以推出一个柿子：

 

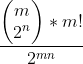
将其化简可以得到：

 

 

 

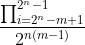
然后我们只需要先用快速幂处理出$$2^n 2^{nm}$$表示分母，然后我们可以发现每1000003个数就有一个1000003的倍数，则如果分子上面累乘的个数大于1000003，那么在累乘过程中应定会出现0，则所有数都是0，分子为0。如果m<1000003就直接暴力求解

然后我们求的是分子和分母的最简形式，考虑约分。

我们发现分母的质因数全是2，那么我们只要找到分子里面质因数分解后有几个2就行。那么怎么找？我们可以将每个2^n减去的那一个数改写为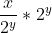形式这样的话如果x中有y个2，其最终结果分式那边一定是个奇数，那么从2^n中提取一个2^y剩下一个偶数减去刚才的奇数得一个奇数，则可以按这种方法一直找到所有2的个数。记得不要忘记用乘法逆元！！

#include<bits/stdc++.h>
#define int long long
#define write(X) printf("%lld ",X)
using namespace std;
inline int read(){
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}

const int mod=1e6+3;
int n,m,a,b,c,d,ans1,ans2;
inline int qmo(int a,int b){
    int ans=1,c=mod; a%=c;
    while(b){
        if(b&1) ans=(ans*a)%c;
        a=(a*a)%c;
        b>>=1;
    } return ans;
}
namespace WSN{
    inline int main(){
        n=read();m=read();
        d=a=qmo(2,n%(mod-1));
        b=qmo(a,m%(mod-1));
        int inv2=500002,num2=n;
        for(int i=1;i<m;i++){
            d=d*(a-i)%mod;
            if(!d) break;
        }
        for(int i=1;(1ll<<i)<=m-1;i++){
            num2+=(m-1)/(1ll<<i);
        }
        c=qmo(inv2,num2);
        d=d*c%mod;
        b=b*c%mod;
        ans1=(b-d+mod)%mod;
        ans2=b%mod;
        write(ans1); write(ans2);
        return 0;
    }
}
signed main(){return WSN::main();}

T3 seq

这题上来一看，我去，根本想不到用什么方面的知识。结果，还真不用什么知识，就是个模拟（但就是不会。。。）。

记录一个up，down分别表示最优及最劣情况，每个开一个pair（x，y）表示那一位数的值，以及使用那个数的个数。

然后正向预处理出本应得到的最优，及最劣情况。

具体为如果连续使用了两个同一个数，up就换成新的大数;同理如果大于5个，down的数就更新。

如果遇到有数的空格就进行比较，保证up最优，down最劣即可。

经过小小的思考就可以加上判断不成立的条件。

然后建造一个bin[]桶函数，按照最劣情况填数，如果桶的一个较大值满，则换成小一号的数继续装。

#include<bits/stdc++.h>
#define val first
#define num second
#define int long long
#define write(X) printf("%lld\n",X)
using namespace std;
inline int read(){
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int NN=2e5+500,mod=1e6+3;
int n,a[NN],bin[NN];
pair<int,int> up[NN],down[NN]; 
namespace WSN{
    inline int main(){
        n=read();
        for(int i=1;i<=n;i++) a[i]=read();
        if(a[1]!=1 && a[1]!=0) {printf("-1\n\n");return 0;}
        up[1]=make_pair(1,1); down[1]=make_pair(1,1);
        for(int i=2;i<=n;i++){
            up[i]=up[i-1]; down[i]=down[i-1];
            up[i].num++; down[i].num++;
            if(up[i].num>2) up[i].val++,up[i].num=1;
            if(down[i].num>5) down[i].val++,down[i].num=1;
            if(!a[i]) continue;
            if(up[i].val>a[i]) up[i]=make_pair(a[i],2ll);
            if(down[i].val<a[i]) down[i]=make_pair(a[i],1);
            if(down[i].val>a[i] || up[i].val<a[i]) {printf("-1\n\n");return 0;}
        } 
        for(int i=1;i<=n;i++){
        }
        if(up[n].num==1) up[n].val--,up[n].num=up[n-1].num+1;
        if(up[n].val<down[n].val) {printf("-1\n\n");return 0;}
        a[n]=up[n].val; write(a[n]);
        bin[a[n]]=1;
        for(int i=n-1;i>=1;i--){
            if(!a[i]){
                int v=min(a[i+1],up[i].val);
                if(bin[v]==5) v--;
                a[i]=v;
            }
            bin[a[i]]++;
        }
        for(int i=1;i<=n;i++)
            printf("%lld ",a[i]);
        return 0;
    }
}
signed main(){return WSN::main();}

 END

---

这次考试并未得到自己想要的分数，T1非常可惜，自己想的复杂度是n^2或者nlogn结果出来跟打线段数暴力分一样，哭死好吧，早知道二十分钟线段树把这题干掉直接去打T3了。。。。结果T2，T3都比较蒙敲了暴力水了20分就结束了，可恶。。。。