Noip模拟8 2021.6.17
T1 星际旅行
仔细一看,发现像一个欧拉路(简称一笔画)。
满足“可以一笔画”的条件是:
1.所有点都有偶数条连边;
2.有偶数个点连奇数条边;
满足以上两个条件的任意一个即可一笔画。
然而还要保证图的联通性。就是说如果有一个图,有一些点是孤立的,按照题意也是可行的。但是如果图像是两个不同的区域,每个区域的点互不连
这种情况就是假的,直接输出零。
因为双向边,我们不妨把每条边看作有两条。那么满足题目情况有三种:
1.去掉任意两个自环;
2.去掉一个自环和任意一条边;
3.去掉连在一个点上的任意两条边;

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 const int NN=100005; 5 int n,m,cnt,ans,out[NN]; 6 bool vis[NN]; 7 struct SNOW{int to,next;}; SNOW e[NN<<1]; int r[NN<<1],tot; 8 inline void add(int x,int y){e[++tot]=(SNOW){y,r[x]}; r[x]=tot;} 9 inline void dfs(int x){ 10 vis[x]=true; 11 for(int i=r[x];i;i=e[i].next) 12 if(!vis[e[i].to]) dfs(e[i].to); 13 } 14 namespace WSN{ 15 inline int main(){ 16 scanf("%lld%lld",&n,&m); 17 for(int i=1,x,y;i<=m;i++){ 18 scanf("%lld%lld",&x,&y); 19 if(x==y) {cnt++;continue;} 20 add(x,y); add(y,x); 21 out[x]++; out[y]++; 22 } 23 ans+=cnt*(cnt-1)/2+cnt*tot/2; 24 for(int i=1;i<=n;i++) if(out[i]) {dfs(i);break;} 25 if(!tot) {cout<<0<<endl; return 0;} 26 for(int i=1;i<=n;i++) if(!vis[i] && out[i]){cout<<0<<endl; return 0;} 27 for(int i=1;i<=n;i++) ans+=out[i]*(out[i]-1)/2; 28 printf("%lld\n",ans); 29 return 0; 30 } 31 } 32 signed main(){return WSN::main();}
T2 砍树
一看这题发现暴力很好打,就飞快得抡了一发暴力上去,但是循环范围开小了(重点是后来不知咋的发现好像没有排序的必要,把排序delete掉了),所以真正的暴力能拿到10分,然而在打暴力时发现二分并无正确性(因为没有单调性,可能每四天比每五天优,而第六天比第四天更优,这也是我第一层循环到头不停的理由),然而二分却能拿到30。。。。小马瞬间meng bi 好吧

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 const int NN=101; 5 int n,K,tr[NN],ans; 6 namespace WSN{ 7 inline int main(){ 8 scanf("%lld%lld",&n,&K); 9 for(int i=1;i<=n;i++) scanf("%lld",&tr[i]); 10 sort(tr+1,tr+n+1); 11 for(int i=1;i<=tr[1]+K;i++){ 12 int tmp=0,vis[NN]={}; 13 for(int j=i;j<=tr[1]+K;j+=i){ 14 for(int k=1;k<=n;k++){ 15 if(tr[k]<=j && !vis[k]){ 16 tmp+=j-tr[k]; 17 vis[k]=true; 18 } 19 if(tmp>K) break; 20 } 21 if(tmp>K) break; 22 } 23 if(tmp<K) ans=i; 24 } 25 printf("%lld\n",ans); 26 return 0; 27 } 28 } 29 signed main(){return WSN::main();}
然而正解是推一个柿子:
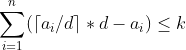
预处理一个: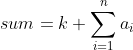
则柿子转化为: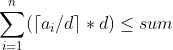
看出这是一个天花板函数,图像很好画,他的每一定值区域的最右端点就是天数的最优解(用右端点坐标结论),还要满足小于等于sum

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 const int NN=101; 5 int n,K,tr[NN],ans,tot,l,r; 6 inline bool judge(int d){ 7 int cnt=0; 8 for(int i=1;i<=n;i++) cnt+=ceil((double)tr[i]/d); 9 if(cnt*d>tot) return 0; 10 else return 1; 11 } 12 namespace WSN{ 13 inline int main(){ 14 scanf("%lld%lld",&n,&K); 15 for(int i=1;i<=n;i++) scanf("%lld",&tr[i]),tot+=tr[i]; 16 tot+=K; 17 for(l=1;l<=tot;l=r+1){ 18 r=tot/(tot/l); 19 if(judge(r)) ans=r; 20 } 21 printf("%lld\n",ans); 22 return 0; 23 } 24 } 25 signed main(){return WSN::main();}
T3 超级树
一看题,看不懂,考场上打了个预处理就跳走了,拿了个小点儿分,当时想着估计是个dp,后来也没多想,光看第四题有无问题了,结果。。。
设dp[i][j]表示i_超级树有j条点不重复路径的方案数。考虑dp[1]对dp[i+1]的贡献。
首先设l表示左子树的合法路径条数,r同理。记录一个num=dp[i][l]*dp[i][r]。
有非常容易想到的几种情况:
1.什么也不做 dp[i+1][l+r]+=num
2.根自己作为一条新路径 dp[i+1][l+r+1]+=num
3.根连接到左子树(或右子树)的某条路径上 dp[i+1][l+r]+=2*num*(l+r)
4.根连接左子树和右子树的各一条路径 dp[i+1][l+r-1]+=2*num*l*r
5.根连接左子树(或右子树)的两条路径 dp[i+1][l+r-1]+=num*(l*(l-1)+r*(r-1))
起始:dp[1][0]=dp[1][1]=1;
目标:dp[k][1];

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 int k,p,dp[301][301]; 5 namespace WSN{ 6 inline int main(){ 7 scanf("%lld%lld",&k,&p); 8 dp[1][0]=dp[1][1]=1; 9 for(int i=0;i<k;i++) 10 for(int j=0;j<k;j++) 11 for(int l=0;l<=j;l++){ 12 int r=j-l,num=dp[i][l]*dp[i][r]%p; 13 dp[i+1][l+r]=(dp[i+1][l+r]+num+2*num*(l+r))%p; 14 dp[i+1][l+r+1]=(dp[i+1][l+r+1]+num)%p; 15 dp[i+1][l+r-1]=(dp[i+1][l+r-1]+num*(l*(l-1)+r*(r-1))+2*num*l*r)%p; 16 } 17 printf("%lld\n",dp[k][1]); 18 return 0; 19 } 20 } 21 signed main(){return WSN::main();}
T4 求和
本次考试败点,傻der的一批
一看第四题,挺可做的,(前提是前二道题抡上部分分,第三题不太可做),就是lca板子忘了,不过好说,还有dfs,可以暴力求解,但是太慢了怎么办,可以特判几种情况加速:
1.有一个点是1,直接找爹推到根;
2.x=y,直接快速幂
3.如果x,y深度一样,lca就是他们上一层。。。。。。(哎,我当时咋没有举出反例呢?多组数据查询,好,于是就这样爆零了)
样例里不是满二叉树,这样的话3情况是假的无法可知,试了样例中树的各种lca,就是没换一个树试试,然后就痛失100分呗。
再就是lca板子一直打的是在线算法,四个函数,倍增处理循环还贼麻烦,要是当时打雨天的尾巴用树链剖分或者树上倍增,就不用费劲特判了
哎,还是做题的时候要好好做,用一些自己背过的板子。。。。草
这里给出树上倍增的lca

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 inline int read(){ 5 int x=0,f=1; char ch=getchar(); 6 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 7 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } 8 return x*f; 9 } 10 11 const int NN=3000005,p=998244353; 12 int n,m,d[NN],f[NN][20],t; 13 queue<int> q; 14 struct SNOW{int to,next;}; SNOW e[NN<<1]; int r[NN<<1],tot; 15 inline void add(int x,int y){e[++tot]=(SNOW){y,r[x]}; r[x]=tot;} 16 inline int qmo(int a,int b){ 17 int ans=1; a%=p; 18 while(b){ 19 if(b&1) ans=(ans*a)%p; 20 b>>=1; a=(a*a)%p; 21 } return ans; 22 } 23 inline void bfs(){ 24 q.push(1); d[1]=0; 25 while(!q.empty()){ 26 int x=q.front(); q.pop(); 27 for(int i=r[x];i;i=e[i].next){ 28 int y=e[i].to; 29 if(y==1||d[y]) continue; 30 d[y]=d[x]+1; 31 f[y][0]=x; 32 for(int j=1;j<=t;j++) 33 f[y][j]=f[f[y][j-1]][j-1]; 34 q.push(y); 35 } 36 } 37 } 38 inline int lca(int x,int y){ 39 if(x==1||y==1) return 1; 40 if(d[x]>d[y]) swap(x,y); 41 for(int i=t;i>=0;i--) 42 if(d[f[y][i]]>=d[x]) y=f[y][i]; 43 if(x==y) return x; 44 for(int i=t;i>=0;i--) 45 if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; 46 return f[x][0]; 47 } 48 namespace WSN{ 49 inline int main(){ 50 n=read(); 51 for(int i=1,x,y;i<n;i++){ 52 x=read(),y=read(); 53 add(x,y); add(y,x); 54 } 55 t=(int)(log(n)/log(2))+1; 56 bfs(); 57 m=read(); 58 while(m--){ 59 int x=read(),y=read(),z=read(); 60 int LCA=lca(x,y),ans=0; 61 for(int i=d[LCA];i<=d[x];i++) ans=(ans+qmo(i,z))%p; 62 for(int i=d[LCA]+1;i<=d[y];i++) ans=(ans+qmo(i,z))%p; 63 printf("%lld\n",ans); 64 } 65 return 0; 66 } 67 } 68 signed main(){return WSN::main();}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号