2025省选模拟9

推歌

《比翼の羽根》

远ざかる云の合间【在渐变渐远的云间】
降り注ぐ辉きは谁を照らす?【倾注而下的光辉会照亮谁?】

夏の日の影を连れて飞び立つ【带着夏日的余影展翅高飞】
想いはまだここに【思念仍遗留于此】

残った痛みはいつか【那些残余的痛楚】
消えて行くから【总有一天会抚平】
もう何も迷わない【再没有任何顾虑】

青空を越えて【穿越蓝天】
昨日よりももっと近付けたら【希望比昨日飞得更远】
少しでいいの微笑んで【一点点就好微笑吧】
风に乗って【乘着轻风】
この心がずっと自由なまま【让这心灵始终自由】
同じ空の下触れ合えるのなら【如若在同片天空下彼此触碰】
どこまでもまっすぐな気持ちで【就以坦然直率的心情】
いつまでも続いてく光で【以无限延伸的光芒】
全てを包みたいから【包围所有一切】

见上げてる云の白に【抬头仰望蓝空白云】
透明な辉きは何を映す?【透明的光辉映照出何物?】

懐かしい梦を连れて羽ばたく【带上怀念的梦翱翔远空】
憧れを手にして【握紧理想】

过ごした季节はいつも【轮回变迁的季节】
侧にあるから【一直陪在左右】
もう涙はいらない【不再需要泪水】
青空に溶けて【溶入蓝天】
优しいままその名前呼べたら【如若温柔轻呼你的名字】
少しでいいの振り向いて【一点点就好请回应我】
风の中で【清风之中】
この心が望んでいる场所を【这颗心深切期望的地方】
広い空の下见付けられたなら【若能在广阔的天空下找到的话】
谁よりも新しい気持ちで【就以无比崭新的心情】
何よりも柔らかい光で【以极致柔和的光芒】
全てを届けたいから【传达所有一切】

雫のように心を揺らす【仿佛水滴摇曳心田】
微かな思い出【微弱的回忆】
それだけ持って【仅是怀着这思念】
止まらずに向かうよ【勇往直前永不停息】

このまま青空を越えて【就这样穿越蓝天】
昨日よりももっと近付けたら【希望比昨日飞得更远】
少しでいいの微笑んで【一点点就好微笑吧】
风に乗って【乘着轻风】
この心がずっと自由なまま【让这心灵始终自由】
同じ空の下触れ合えるのなら【如若在同片天空下彼此触碰】
どこまでもまっすぐな気持ちで【就以坦然直率的心情】
いつまでも続いてく光で【以无限延伸的光芒】
全てを包みたいから【包围所有一切】

2025省选模拟9

网络流专场是吧😅

Delov 的 npy 们原题链接

一眼网络流，然后不会了。

发现正常顺着限制做做不了，考虑将限制转化一下，以 L 操作为例。

在 \(a_i\) 左侧的点中不超过 \(b_i\) 个，等价于从左往右数第 \(b_i+1\) 个点在 \(a_i\) 右侧。

但还是不好做，考虑枚举选择的点的个数，这样就可以知道选择的第 \(i\) 个点应该所处的区间。

然后就是网络流经典操作——拆点。

将一个点拆成两个点，一个为横坐标，一个为纵坐标，中间连边容量为 \(1\)，费用为 \(w\)，如果横坐标在第 \(i\) 个点可以的范围内，那么就将该点和横坐标和第 \(i\) 个点连边，如果纵坐标在第 \(i\) 个点范围内，那么就将该点的纵坐标与第 \(i\) 个点相连。

说的不太好，还是看图吧。

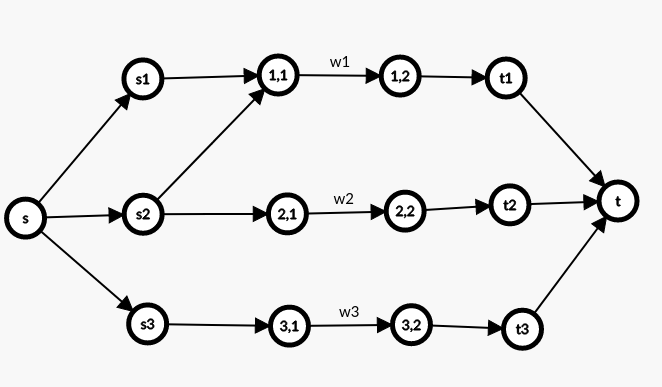
容量都为 \(1\)，若非标注，则费用为 \(0\)。

\(s\) 是超级源点，\(sk\) 表示横坐标第 \(k\) 个点，\((i,1/2)\) 表示第 \(i\) 个点拆点， \(tk\) 表示纵坐标第 \(k\) 个点，\(t\) 为超级汇点。

再不懂就自行理解吧，语文不好，实在不会说了。

code

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
  auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
  auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
#define ep emplace
const int N = 100010;
int a[N],b[N],c[N],d[N],x[N],y[N],n,m;
int s,t;ll w[N];
template<size_t N,size_t M>
struct Graph{
  struct E{int to,n,w;ll c;}e[M];
  int h[N],ct = 1;
  void add(int u,int v,int w,ll c){
    e[++ct] = {v,h[u],w,c};h[u] = ct;
  }
  void clear(){ct = 1;rep(i,0,N-1,1) h[i] = 0;}
#define repe(i,x,y,g) for(int i = g.h[x],y = g.e[i].to;i;i = g.e[i].n,y = g.e[i].to)
};Graph<N,N> g;
ll dist[N];bool vis[N];int now[N];
bool bfs(int s = s){
  rep(i,s,t,1) dist[i] = -1e18,vis[i] = false,now[i] = g.h[i];
  queue<int> q;q.ep(s);vis[s] = true;dist[s] = 0;
  while(q.size()){
    int x = q.front();q.pop();vis[x] = false;
    repe(i,x,y,g){
      int w = g.e[i].w;ll c = g.e[i].c;
      if(!w) continue;
      if(dist[y] < dist[x] + c){
        dist[y] = dist[x] + c;
        if(!vis[y]) vis[y] = true,q.ep(y);
      }
    }
  }
  return dist[t] != -1e18;
}
int dinic(int x,int flow){
  if(x == t || !flow) return flow;
  int res = 0;vis[x] = true;
  for(int i = now[x];i && flow;i = g.e[i].n){
    now[x] = i;
    int w = g.e[i].w,y = g.e[i].to;ll c = g.e[i].c;
    if(!w) continue;
    if(vis[y]) continue;
    if(dist[y] == dist[x] + c){
      int k = dinic(y,min(flow,w));
      g.e[i].w -= k;g.e[i^1].w += k;
      res += k;flow -= k;
    }
  }
  return res;
}
pair<int,ll> MaxCostFlow(){
  int maxflow = 0;ll maxcost = 0;
  while(bfs()){
    int k = dinic(s,1e9);
    maxflow += k;
    maxcost += dist[t]*k;
  }
  return make_pair(maxflow,maxcost);
}
ll calc(int k){
  g.clear();
  s = 0,t = 2*k+2*n+1;
  rep(i,1,k,1){
    g.add(s,i,1,0);g.add(i,s,0,0);
    g.add(i+2*n+k,t,1,0);g.add(t,i+2*n+k,0,0);
  }
  rep(i,1,n,1){
    g.add(i+k,i+k+n,1, w[i]);
    g.add(i+k+n,i+k,0,-w[i]);
    rep(j,1,k,1){
      if(a[j] <= x[i] && x[i] <= b[k-j+1]) g.add(j,i+k,1,0),g.add(i+k,j,0,0);
      if(c[j] <= y[i] && y[i] <= d[k-j+1]) g.add(i+k+n,j+k+n*2,1,0),g.add(j+k+n*2,i+k+n,0,0);
    }
  }
  return MaxCostFlow().second;
}
signed main(){
  cin.tie(nullptr)->sync_with_stdio(false);
  memset(b,0x3f,sizeof b);
  memset(d,0x3f,sizeof d);
  cin>>n;rep(i,1,n,1) cin>>x[i]>>y[i]>>w[i];cin>>m;
  rep(i,1,m,1){
    char op;int x,y;cin>>op>>x>>y;y++;
    if(op == 'L') a[y] = max(a[y],x+1);
    if(op == 'R') b[y] = min(b[y],x-1);
    if(op == 'D') c[y] = max(c[y],x+1);
    if(op == 'U') d[y] = min(d[y],x-1);
  }
  rep(i,1,n,1) 
    a[i] = max(a[i],a[i-1]),b[i] = min(b[i],b[i-1]),
    c[i] = max(c[i],c[i-1]),d[i] = min(d[i],d[i-1]);
  ll ans = 0;
  rep(i,0,n,1) ans = max(ans,calc(i));
  cout<<ans<<'\n';
}

皮胚原题链接

以 popcount 的奇偶性分组，然后发现就变成了二分图了。

但是点数是 \(O(2^n)\) 的，边数是 \(O(n\times 2^n)\) 的，显然过不了，考虑缩小点的数量和边的数量。

我们发现每个点会与 \(n\) 个人相连，那么每匹配一对就会让剩下匹配的方案数最多减少 \(2\times (n−1)\)（这两个人都不能与他另外 \(n−1\) 个与其仅有一个观点不同的人匹配），加上这两个人匹配的这条边总共减少\(2\times n−1\)，所以说假如匹配 \(k\) 次最多只会减少 \(k\times (2\times n−1)\) 种匹配方式，也就是假如选择 \(k\times(2\times n−1)\) 个匹配那么至少会存在 \(k\) 种匹配方式。

那么只需要取前 \(k\times (2\times n-1)\) 条边即可。用 std::nth_element 可以在 \(O(n)\) 的时间求出。

然后跑二分图最大权匹配就行。

但是常规的二分图最大权匹配要将左部点和汇点连一条边，本题因为有特殊性质所以不用。（特殊性质是两点之间的边权为两点点权和，为什么不用自行思考）

code

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
  auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
  auto I = freopen("pp.in","r",stdin),O = freopen("pp.out","w",stdout);
  //auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
#define ppc __builtin_popcount
#define ep emplace
const int N = 1e6 + 60000,M = 1e5;
template<size_t N,size_t M>
struct Graph{
  struct E{int to,n;ll w,c;}e[M];
  int h[N],ct = 1;
  void add(int u,int v,ll w,ll c){
    e[++ct] = {v,h[u],w,c};
    h[u] = ct;
  }
#define repe(i,x,y,g) for(int i = g.h[x],y = g.e[i].to; i;i = g.e[i].n,y = g.e[i].to)
};Graph<N,M> g;
int n,k,a[N],tot,ttt,s,t,_s,bel[N];
struct node{int v,x,y;}edge[N*20];
int now[N];ll dist[N];bool vis[N];
bool bfs(int s = s){
  rep(i,1,tot,1) dist[i] = -1e18,now[i] = g.h[i],vis[i] = false;
  queue<int> q;q.push(s);vis[s] = true;dist[s] = 0;
  while(q.size()){
    int x = q.front();q.pop();vis[x] = false;
    repe(i,x,y,g){
      auto w = g.e[i].w,c = g.e[i].c;
      if(!w) continue;
      if(dist[y] < dist[x] + c){
        dist[y] = dist[x] + c;
        if(!vis[y]) q.ep(y),vis[y] = true;
      }
    }
  }
  return dist[t] != -1e18;
}
int dinic(int x,int flow){
  if(x == t || !flow) return flow;
  ll res = 0;
  vis[x] = true;
  for(int i = now[x]; i&&flow;i = g.e[i].n){
    now[x] = i;
    int y = g.e[i].to,w = g.e[i].w;
    ll cost = g.e[i].c;
    if(!w) continue;
    if(vis[y]) continue;
    if(dist[y] == dist[x] + cost){
      int k = dinic(y,min(flow,w));
      g.e[i].w -= k;g.e[i^1].w += k;
      res += k;flow -= k;
    }
  }
  return res;
}
pair<int,ll> MaxCostFlow(){
  int maxflow = 0;ll maxcost = 0;
  while(bfs()){
    ll k = dinic(s,1e9);
    if(!k) break;
    maxflow += k;maxcost += dist[t]*k;
  }
  return make_pair(maxflow,maxcost);
}
signed main(){
  cin.tie(nullptr)->sync_with_stdio(false);
  cin>>n>>k;rep(i,0,(1<<n)-1,1) cin>>a[i];
  rep(i,0,(1<<n)-1,1){
    rep(j,0,n-1,1){
      int p = i^(1<<j);
      if(p >= i) continue;
      edge[++ttt] = (node){a[i]+a[p],i,p};
    }
  }
  s = ++tot,t = ++tot,_s = ++tot;
  g.add(s,_s,k,0);
  g.add(_s,s,0,0);
  int req = k*(2*n-1);
  if(req > ttt) req = ttt;
  nth_element(edge+1,edge+1+req,edge+1+ttt,[](const node &x,const node &y){return x.v > y.v;});
  rep(i,1,req,1){
    auto p = edge[i];
    if(ppc(p.x)%2 == 0) swap(p.x,p.y);
    if(!bel[p.x]) bel[p.x] = ++tot,g.add(_s,bel[p.x],1,0),g.add(bel[p.x],_s,0,0);
    if(!bel[p.y]) bel[p.y] = ++tot,g.add(bel[p.y],t,1,0),g.add(t,bel[p.y],0,0);
    g.add(bel[p.x],bel[p.y],1, p.v);
    g.add(bel[p.y],bel[p.x],0,-p.v);
  }
  cout<<MaxCostFlow().second<<'\n';
}

流（flow）原题链接

不会，不想打了。

今天是春日野穹生日捏。

posted @ 2025-02-05 19:40 CuFeO4 阅读(28) 评论(0) 编辑收藏举报

刷新页面返回顶部

Cu

半退役

2025省选模拟9