day13
1、二叉树理论基础篇
-
二叉树的种类
- 满二叉树:二叉树的所有叶子节点都在最后一层,并且节点总数为2^n-1,n为层数【从1 开始】
- 完全二叉树:二叉树的所有叶子节点都在最后一层或者倒数第二层,且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,则该二叉树为完全二叉树。
- 二叉搜索树(二叉排序树)【有序树】
- 对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。如果有相同的值,可以将该节点放在左子节点或者右子节点
- 平衡二叉树(平衡二叉搜索树)
- 它是一颗空树或他的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
-
二叉树的存储方式
-
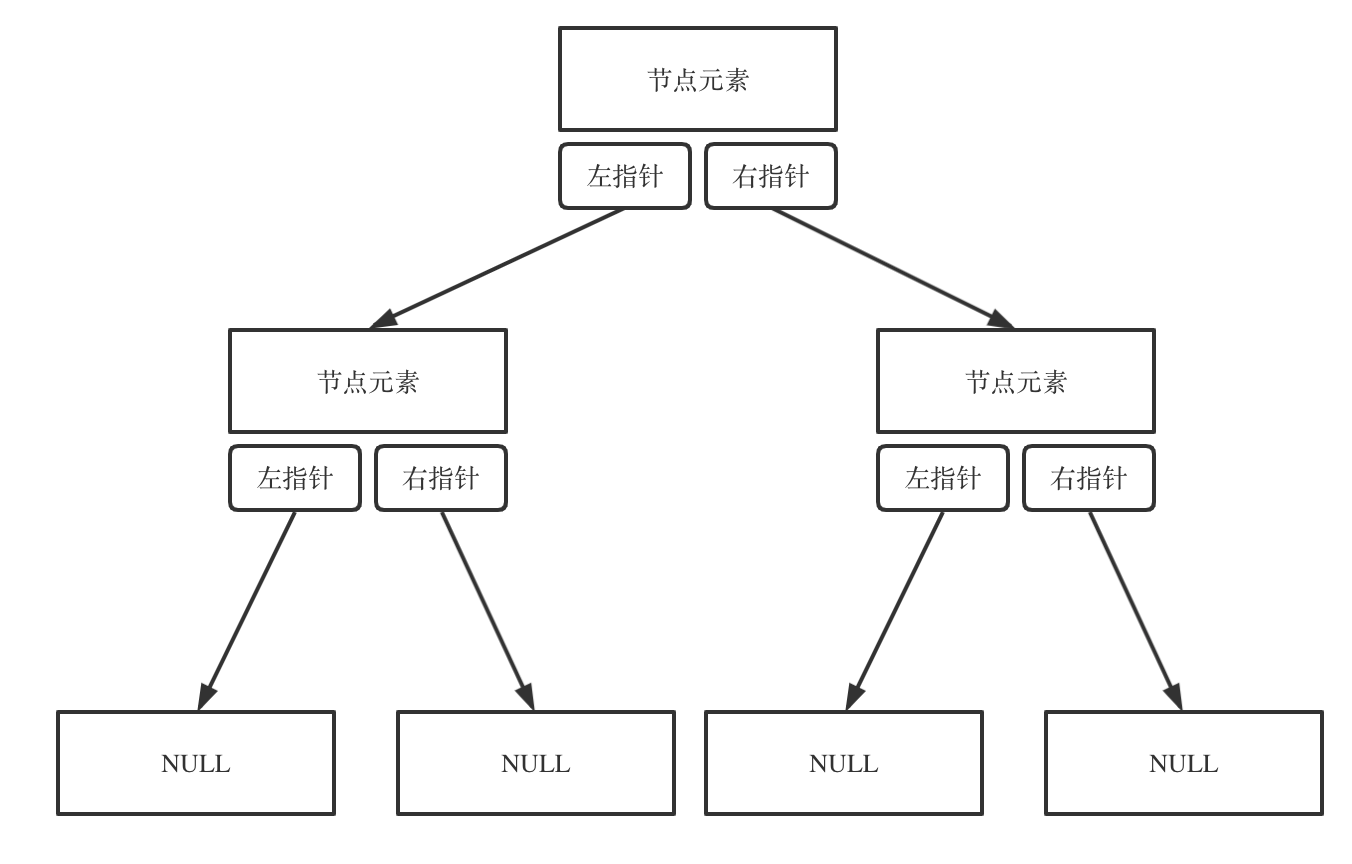
链式存储【使用指针】
![img]()
-
顺序存储【使用数组】
- 顺序存储二叉树通常只考虑完全二叉树
- 第n个元素的左子节点下标为:2*n+1
- 第n个元素的右子节点下标为:2*n+2
- 第n个元素的父节点下标为:(n-1)/ 2
- 注意:n表示二叉树的第几个元素(从0开始编号)
-
-
二叉树的的遍历方式
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历:一层一层的去遍历。
- 层次遍历(迭代法)
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
-
堆
-
堆是具有以下性质的完全二叉树:
-
每个节点的值都大于或等于其左右子节点的值,称为大顶堆。
- 注意:没有要求节点的左子节点的值与右子节点的值的关系
-
每个节点的值都小于或等于其左右子节点的值,称为小顶堆。
-
-
大顶堆特点
- arr[i] > = arr[2i + 1] && arr[i] > = arr[2i + 2]
-
小顶堆特点
- arr[i] <= arr[2i + 1] && arr[i] < = arr[2i + 2]
-
对数组进行升序排序:采用大顶堆;对数组进行降序排序:采用小顶堆
-
2、递归遍历
//前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
preOrder(root, res);
return res;
}
public void preOrder(TreeNode root,List<Integer> res){
if(root == null){
return;
}
res.add(root.val);
preOrder(root.left, res);
preOrder(root.right, res);
}
}
//中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
inOrder(root,res);
return res;
}
public void inOrder(TreeNode root, List<Integer> res){
if(root == null){
return;
}
inOrder(root.left, res);
res.add(root.val);
inOrder(root.right, res);
}
}
//后序遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
postOrder(root,res);
return res;
}
public void postOrder(TreeNode root, List<Integer> res){
if(root == null){
return;
}
postOrder(root.left, res);
postOrder(root.right, res);
res.add(root.val);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号