浅谈kdtree
Ⅰ、抛出问题
Description
有一列元素,每一个元素有三个属性:标号、标识符、数值。这些元素按照标号从1n排列,标识符也是1n的一个排列,初始时数值为0。当然我们可以把每个元素看成一个多维数字,那么这列元素就是一个数列。
现在请你维护这个数列,使其能支持以下两种操作:1.将标号为lr的所有元素的数值先乘上x,再加上y;2.将标识符为lr的所有元素的数值先乘上x,再加上y。当然你还得回答某些询问:1.标号为lr的所有元素的数值的和;2.标识符为lr的所有元素的数值的和。
Input
第一行有两个正整数n、m,分别表示数列长度和操作与询问个数的总和。第二行有n个正整数,表示每个元素的标识符,保证这n个数是1~n的一个排列。接下来m行,每行的第一个数字为op。若op为0,则表示要进行第一个操作,接下去四个数字表示l,r,x,y;若op为1,则表示要进行第二个操作,接下去四个数字表示l,r,x,y;若op为2,则表示要回答第一个询问,接下去两个数字表示l,r;若op为3,则表示要回答第二个询问,接下去两个数字表示l,r。
Output
包含若干行,每行表示一个询问的答案。由于答案可能很大,只要请你输出答案对536870912取模后的值即可。
Sample Input
4 4
2 1 4 3
0 2 3 4 5
1 1 3 4 7
2 1 1
3 1 1
Sample Output
7
27
HINT
第一次操作后,数列变为0 5 5 0
第二次操作后,数列变为7 27 5 7
N,M<=50000, 1<=L<=R<=N 0<=X,Y<=2^31-1
Source
bzoj4303数列
Ⅱ、分析问题
kdtree,全称k-dimensional-tree,意思即为k维树,主要用于解决高维空间的修改查询操作,支持打标记,求最近最远点对等,类似于线段树等数据结构,接下来就来详细讲讲kdtree的写法
1、维护的数据
写数据结构,一定要弄清维护了哪些数据
kdtree是一种类似于线段树一样的数据结构,树上每一个节点管辖k维区间中的某一个范围,存每个维度的最大最小值以确定边界
代码:
注:代码中给的是二维kdtree的模板,所以只有两位
struct hahaha{
int tp,ls,rs,v[2],Max[2],Min[2],val;//tp为当前节点维护的是哪一维,ls,rs分别为左右儿子编号,v存节点坐标,Max和Min维护当前节点管辖区间的最大最小(即边界),val存当前点的权值
int cnt,mlt,sum,len;//cnt加标记,mlt乘标记,sum区间和,len区间长度
bool operator<(const hahaha &y)const{
return v[T]<y.v[T];//排序方便寻找中位数
}
}tree[50010];
2、建树
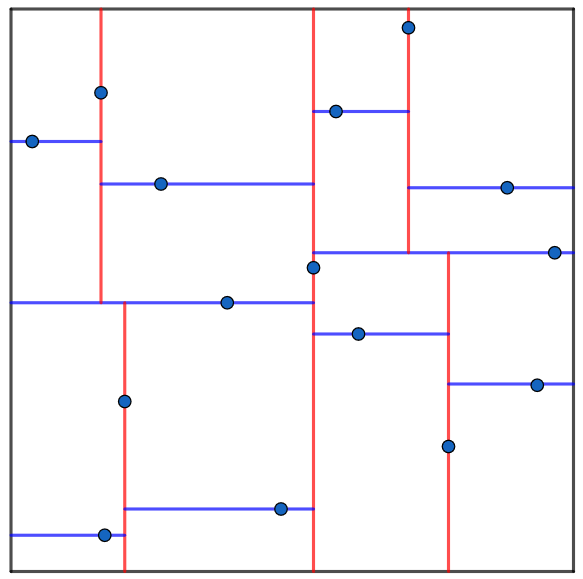
如图,可以看出,kdtree是以一位一位顺次分割的方式建树的,
每次寻找区间中的中位数点,沿当前维度进行分割,如本图为先竖着再横着分割
第一次先找到横向的中位数,竖着分割一次(已用红色标出),在递归左右子树,找竖着的中位数,横向分割,再往下依次递归
以下建树部分代码:
inline void updata(int p){//很显然的更新
tree[p].Min[0]=min(tree[p].v[0],min(tree[ls(p)].Min[0],tree[rs(p)].Min[0]));//x坐标的最小值
tree[p].Min[1]=min(tree[p].v[1],min(tree[ls(p)].Min[1],tree[rs(p)].Min[1]));//y坐标的最小值
tree[p].Max[0]=max(tree[p].v[0],max(tree[ls(p)].Max[0],tree[rs(p)].Max[0]));//x坐标的最大值
tree[p].Max[1]=max(tree[p].v[1],max(tree[ls(p)].Max[1],tree[rs(p)].Max[1]));//y坐标的最大值
}
inline int build_tree(int l,int r,int tp){//l,r为区间,tp为区间维度
T=tp;//T也是区间维度,用于查找中位数
int mid=((l+r)>>1),p=mid;
nth_element(tree+l,tree+mid,tree+r+1);//这是个查找中位数的神奇函数
tree[p].tp=tp;
tree[p].mlt=1;
tree[p].len=r-l+1;//更新节点信息
if(l<mid)
ls(p)=build_tree(l,mid-1,tp^1);//其实这个地方严谨来说应该是(tp+1)%2,因为维度是顺次遍历,假如说有5维,那就是按照0,1,2,3,4,0,1,2...这样的顺序遍历。
//注意,这里不是像线段树一样l,mid,而是l,mid-1,因为左区间不包括这个点本身
//之所以这样写是为了卡常
if(r>mid)
rs(p)=build_tree(mid+1,r,tp^1);
updata(p);//再次更新节点信息
return p;
}
3、修改操作
修改操作指的是将在某个范围内的所有节点的权值更改,支持像线段树一样打标记和下传标记
具体见代码
//注:本题要求的是先乘上一个数再加上一个数,所以有两个标记数组
inline void Add_mlt(int p,int v){
tree[p].val*=v;
tree[p].cnt*=v;
tree[p].mlt*=v;
tree[p].sum*=v;
}
inline void Add_cnt(int p,int v){
tree[p].val+=v;
tree[p].cnt+=v;
tree[p].sum+=tree[p].len*v;
}
inline void pushdown(int p){
if(tree[p].mlt!=1){//下传乘标记
Add_mlt(ls(p),tree[p].mlt);
Add_mlt(rs(p),tree[p].mlt);
tree[p].mlt=1;
}
if(tree[p].cnt!=0){//下传加标记
Add_cnt(ls(p),tree[p].cnt);
Add_cnt(rs(p),tree[p].cnt);
tree[p].cnt=0;
}
}
inline void change(int p,int x,int y,int mt,int ct){//p为当前节点,将第T维(T为全局变量,记录当前处理维度)坐标在x与y之间的数都乘上mt,加上ct
if(tree[p].Max[T]<x||y<tree[p].Min[T])//如果不在要处理的范围内,退出
return ;
if(x<=tree[p].Min[T]&&tree[p].Max[T]<=y){//如果都在要处理的范围内,就打上乘标记与加标记
Add_mlt(p,mt);//加乘标记
Add_cnt(p,ct);//加加标记
return ;
}
pushdown(p);//下传标记
if(x<=tree[p].v[T]&&tree[p].v[T]<=y)//如果当前点在处理范围内
tree[p].val=tree[p].val*mt+ct;//处理当前节点
change(ls(p),x,y,mt,ct);//修改左子树
change(rs(p),x,y,mt,ct);//修改右子树
tree[p].sum=tree[ls(p)].sum+tree[rs(p)].sum+tree[p].val;//更新当前节点
}
5、查询操作
详见注释
inline int ask(int p,int x,int y){//查询T维x到y的和
if(tree[p].Max[T]<x||y<tree[p].Min[T])//出范围就return 0
return 0;
if(x<=tree[p].Min[T]&&tree[p].Max[T]<=y)//在范围之内就返回和
return tree[p].sum;
pushdown(p);//下传标记
int res=ask(ls(p),x,y)+ask(rs(p),x,y);//加上左右子树
if(x<=tree[p].v[T]&&tree[p].v[T]<=y)
res+=tree[p].val;//加上这个点本身
return res;
}
至此,kdtree算法的讲解就到此结束,让我们回到原题
容易想到可以吧原题中的i到j看作一维,吧\(p_i\)到\(p_j\)看作第二维,这样就可以看作是在一个二维平面上进行操作
代码(模板):
#include<bits/stdc++.h>
#define F(i,j,n) for(register int i=j;i<=n;i++)
#define INF 0x3f3f3f3f
#define ll long long
#define mem(i,j) memset(i,j,sizeof(i))
using namespace std;
#define Md 536870912
int n,m,T;
inline int read(){
int datta=0;char chchc=getchar();bool okoko=0;
while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
return okoko?-datta:datta;
}
class kd_tree{//之所以用class是为了装逼
private:
public:
#define ls(p) tree[p].ls
#define rs(p) tree[p].rs
int tot,rt;
struct hahaha{
int tp,ls,rs,v[2],Max[2],Min[2],val;
int cnt,mlt,sum,len;
bool operator<(const hahaha &y)const{
return v[T]<y.v[T];
}
}tree[50010];
inline void Add(int *a,int v){
a[0]=a[1]=v;
}
inline void updata(int p){
tree[p].Min[0]=min(tree[p].v[0],min(tree[ls(p)].Min[0],tree[rs(p)].Min[0]));
tree[p].Min[1]=min(tree[p].v[1],min(tree[ls(p)].Min[1],tree[rs(p)].Min[1]));
tree[p].Max[0]=max(tree[p].v[0],max(tree[ls(p)].Max[0],tree[rs(p)].Max[0]));
tree[p].Max[1]=max(tree[p].v[1],max(tree[ls(p)].Max[1],tree[rs(p)].Max[1]));
}
inline int build_tree(int l,int r,int tp){
T=tp;
int mid=((l+r)>>1),p=mid;
nth_element(tree+l,tree+mid,tree+r+1);
tree[p].tp=tp;
tree[p].mlt=1;
tree[p].len=r-l+1;
if(l<mid)
ls(p)=build_tree(l,mid-1,tp^1);
if(r>mid)
rs(p)=build_tree(mid+1,r,tp^1);
updata(p);
return p;
}
inline void init(){
Add(tree[0].Max,-INF);
Add(tree[0].Min,INF);
F(i,1,n)
tree[i].v[0]=i,tree[i].v[1]=read();
rt=build_tree(1,tot=n,0);
}
inline void Add_mlt(int p,int v){
tree[p].val*=v;
tree[p].cnt*=v;
tree[p].mlt*=v;
tree[p].sum*=v;
}
inline void Add_cnt(int p,int v){
tree[p].val+=v;
tree[p].cnt+=v;
tree[p].sum+=tree[p].len*v;
}
inline void pushdown(int p){
if(tree[p].mlt!=1){
Add_mlt(ls(p),tree[p].mlt);
Add_mlt(rs(p),tree[p].mlt);
tree[p].mlt=1;
}
if(tree[p].cnt!=0){
Add_cnt(ls(p),tree[p].cnt);
Add_cnt(rs(p),tree[p].cnt);
tree[p].cnt=0;
}
}
inline void change(int p,int x,int y,int mt,int ct){
if(tree[p].Max[T]<x||y<tree[p].Min[T])
return ;
if(x<=tree[p].Min[T]&&tree[p].Max[T]<=y){
Add_mlt(p,mt);
Add_cnt(p,ct);
return ;
}
pushdown(p);
if(x<=tree[p].v[T]&&tree[p].v[T]<=y)
tree[p].val=tree[p].val*mt+ct;
change(ls(p),x,y,mt,ct);
change(rs(p),x,y,mt,ct);
tree[p].sum=tree[ls(p)].sum+tree[rs(p)].sum+tree[p].val;
}
inline int ask(int p,int x,int y){
if(tree[p].Max[T]<x||y<tree[p].Min[T])
return 0;
if(x<=tree[p].Min[T]&&tree[p].Max[T]<=y)
return tree[p].sum;
pushdown(p);
int res=ask(ls(p),x,y)+ask(rs(p),x,y);
if(x<=tree[p].v[T]&&tree[p].v[T]<=y)
res+=tree[p].val;
return res;
}
}K;
int main(){
n=read();m=read();
K.init();
F(i,1,m){
int opt=read(),l=read(),r=read(),x,y;
if(opt<=1){
x=read();y=read();
T=opt;
K.change(K.rt,l,r,x,y);
}
if(opt>=2){
T=opt-2;
printf("%d\n",K.ask(K.rt,l,r)&(Md-1));//不这么写会T
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号