动态规划-树上dp-时间戳-判断父节点-6103. 从树中删除边的最小分数

2022-06-26 15:43:28

问题描述：

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点， 以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

1. 分别获取三个组件 每个 组件中所有节点值的异或值。
2. 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。

• 例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的 最小 分数。

 

示例 1：

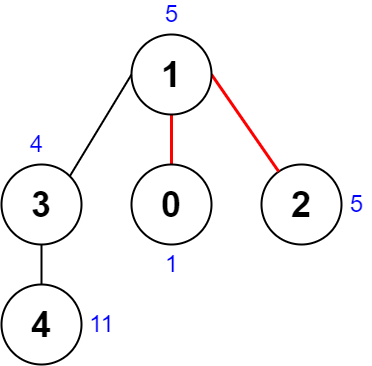
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

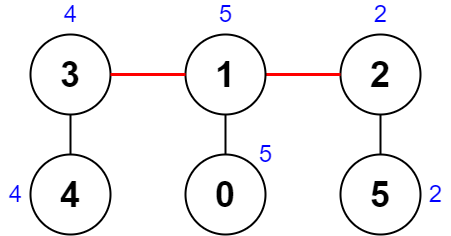
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

 

提示：

• n == nums.length
• 3 <= n <= 1000
• 1 <= nums[i] <= 108
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵有效的树 

问题求解：

本题有个子问题，就是给定两个节点，如何判断是否属于同一子树。这个可以通过时间戳来进行O(1)的求解。

剩余就是暴力遍历删除的两条边，然后分类讨论他们的删除位置关系。

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        n = len(nums)
        graph = defaultdict(set)
        for u, v in edges:
            graph[u].add(v)
            graph[v].add(u)
        
        in_, out, xor, time = [0] * n, [0] * n, [0] * n, 0
        def dfs(x, fa):
            nonlocal time
            time += 1
            in_[x] = time
            xor[x] = nums[x]
            for y in graph[x]:
                if y != fa:
                    dfs(y, x)
                    xor[x] ^= xor[y]
            out[x] = time
        dfs(0, -1)

        def is_fa(x, y):
            return in_[x] <= in_[y] <= out[y] <= out[x]
        
        for e in edges:
            if not is_fa(e[0], e[1]):
                e[0], e[1] = e[1], e[0]
        
        res = float("inf")
        for (x1, y1), (x2, y2) in combinations(edges, 2):
            if is_fa(y1, x2):
                x, y, z = xor[y2], xor[y1] ^ xor[y2], xor[0] ^ xor[y1]
            elif is_fa(y2, x1):
                x, y, z = xor[y1], xor[y2] ^ xor[y1], xor[0] ^ xor[y2]
            else:
                x, y, z = xor[y1], xor[y2], xor[0] ^ xor[y1] ^ xor[y2]
            res = min(res, max(x, y, z) - min(x, y, z))
            
        return res