机器学习经典算法

scikit-learn官网

https://scikit-learn.org

K近邻算法

KNN算法详解 https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html

原理

import numpy as np
from math import sqrt
from collections import Counter


class KNNClassifier:

    def __init__(self, k):
        """初始化kNN分类器"""
        assert k >= 1, "k must be valid"
        self.k = k
        self._X_train = None
        self._y_train = None

    def fit(self, X_train, y_train):
        """根据训练数据集X_train和y_train训练kNN分类器"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        assert self.k <= X_train.shape[0], \
            "the size of X_train must be at least k."

        self._X_train = X_train
        self._y_train = y_train
        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self._X_train is not None and self._y_train is not None, \
                "must fit before predict!"
        assert X_predict.shape[1] == self._X_train.shape[1], \
                "the feature number of X_predict must be equal to X_train"

        y_predict = [self._predict(x) for x in X_predict]
        return np.array(y_predict)

    def _predict(self, x):
        """给定单个待预测数据x，返回x的预测结果值"""
        assert x.shape[0] == self._X_train.shape[1], \
            "the feature number of x must be equal to X_train"

        distances = [sqrt(np.sum((x_train - x) ** 2))
                     for x_train in self._X_train]
        nearest = np.argsort(distances)

        topK_y = [self._y_train[i] for i in nearest[:self.k]]
        votes = Counter(topK_y)

        return votes.most_common(1)[0][0]

    def __repr__(self):
        return "KNN(k=%d)" % self.k

K个最近的节点中，某个类别多的分类多则为该分类

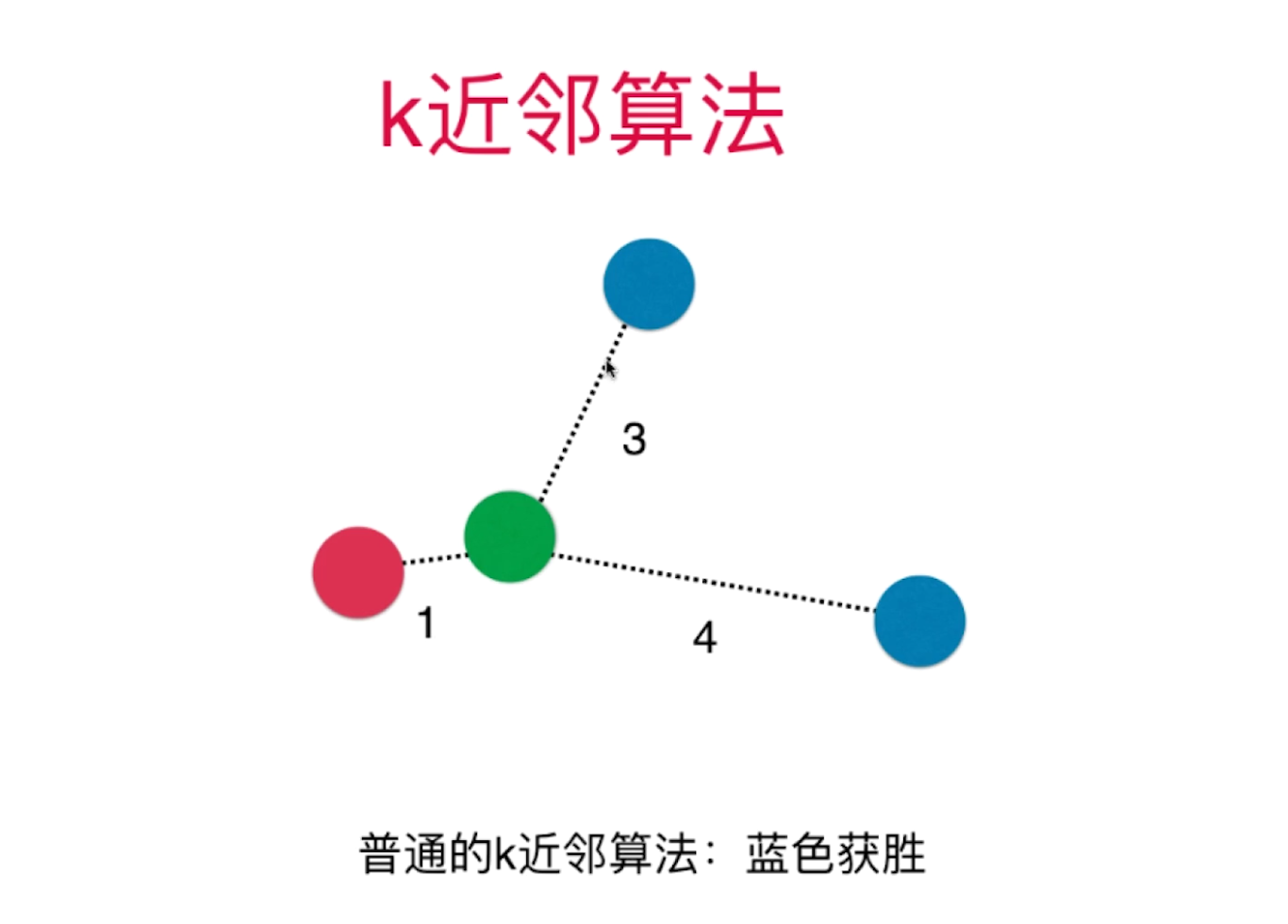
默认参数

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs)

加载数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets 

iris = datasets.load_iris()
iris.keys()

X = iris.data
y = iris.target

X.shape
y.shape

拆分数据集

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

print(X_train.shape)
print(y_train.shape)

print(X_test.shape)
print(y_test.shape)

分类

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=6)
knn_clf.fit(X_train, y_train)

y_predict = knn_clf.predict(X_test)
sum(y_predict == y_test) / len(y_test)  # 准确度

knn_clf.score(X_test, y_test) # 准确度

分类结果的精确度

from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_predict)

　　

# 加载数据集
from sklearn import datasets

digits = datasets.load_digits()

X = digits.data
print(X.shape)  # (1797, 64)

y = digits.target
print(y.shape)  # (1797,)

# 拆分数据集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

# 分类
from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train, y_train)
y_predict = knn_clf.predict(X_test)

# 分类精确度
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_predict))  # 0.9888888888888889

knn_clf.score(X_test, y_test)  # 0.9888888888888889

超参数

weights 考虑距离权重
p 明可夫斯基距离相应的p

如果K=3,投票结果相同，如下三个类别，那怎么办呢？引入距离权重

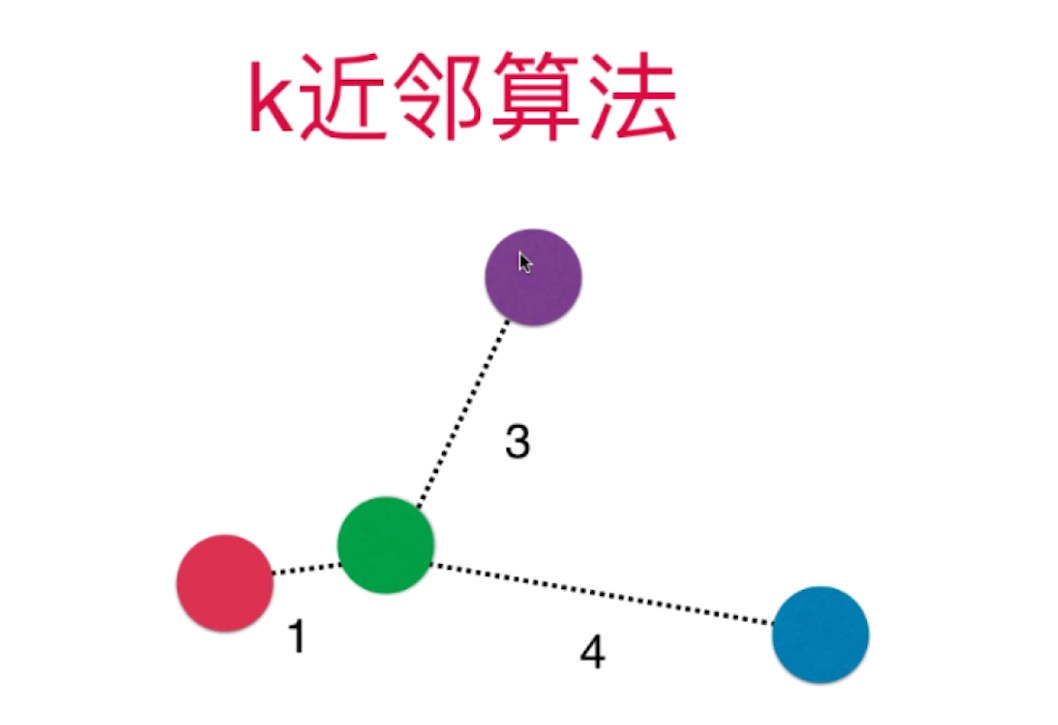
欧拉距离

weights='distance'

p = 2 

best_score = 0.0
best_k = -1
best_method = ""
for method in ["uniform", "distance"]:
    for k in range(1, 11):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_method = method
        
print("best_method =", best_method)  # best_method = uniform 
print("best_k =", best_k)  # best_k = 4
print("best_score =", best_score)  # best_score = 0.9916666666666667

sk_knn_clf = KNeighborsClassifier(n_neighbors=4, weights="distance", p=1)
sk_knn_clf.fit(X_train, y_train)
sk_knn_clf.score(X_test, y_test)  # 0.9833333333333333

明可夫斯基距离

考虑距离权重，最佳的参数p为2

best_score = 0.0
best_k = -1
best_p = -1

for k in range(1, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_p = p
            best_score = score
        
print("best_k =", best_k)  # best_k = 3
print("best_p =", best_p)  # best_p = 2
print("best_score =", best_score)  # best_score = 0.9888888888888889

网格搜索　　

k p结合的搜索　　

verbose 输出日志

param_grid = [
    {
        'weights': ['uniform'], 
        'n_neighbors': [i for i in range(1, 11)]
    },
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(1, 11)], 
        'p': [i for i in range(1, 6)]
    }
]

knn_clf = KNeighborsClassifier()

from sklearn.model_selection import GridSearchCV
grid_search = GridSearchCV(knn_clf, param_grid)

grid_search.fit(X_train, y_train)
grid_search.best_estimator_  
# KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',metric_params=None, n_jobs=1, n_neighbors=3, p=3, weights='distance')

grid_search.best_score_  # 0.9853862212943633

grid_search = GridSearchCV(knn_clf, param_grid, n_jobs=-1, verbose=2)  # n_jobs=-1为所有CPU核
grid_search.fit(X_train, y_train)

　　

更多超参数

http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html

数据归一化 

作用：避免某部分特征数值过大，其它特征影响较小

# 均值方差归一化原理
import numpy as np
import matplotlib.pyplot as plt

X2 = np.random.randint(0, 100, (50, 2))
X2 = np.array(X2, dtype=float)

X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0])
X2[:,1] = (X2[:,1] - np.mean(X2[:,1])) / np.std(X2[:,1])

np.mean(X2[:,0])  # -1.1990408665951691e-16
np.std(X2[:,0])  # 1.0
np.mean(X2[:,1])  # -1.1546319456101628e-16
np.std(X2[:,1])  # 0.99999999999999989

　　

import numpy as np
from sklearn import datasets

# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 拆分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=666)

# 归一化
from sklearn.preprocessing import StandardScaler 
standardScalar = StandardScaler() 
standardScalar.fit(X_train)  # 获得归一化后的均值和方差

standardScalar.mean_  # 归一化的均值
standardScalar.scale_   # 归一化的方差

X_train_standard = standardScalar.transform(X_train)  # 均值方差归一化处理
X_test_standard = standardScalar.transform(X_test) 


# 归一化后的数据进行处理
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train_standard, y_train)
knn_clf.score(X_test_standard, y_test)  # 1.0

总结

优点：

　　1.解决分类问题，天然可以解决多分类问题

　　2.思想简单，效果强大

　　3.还可以解决回归问题(取最近几个点的均值或者加权平均)

　　https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsRegressor.html

缺点：

　　1.最大缺点：效率低下(训练集有m个样本，n个特征，则预测每一个新的数据，需要O(m*n))

　　2.高度数据相关(假设k=3,如果有两个点是错误值，则结果受影响很大)

　　3.预测结果不具可解释性

　　4.维度灾难

　

 

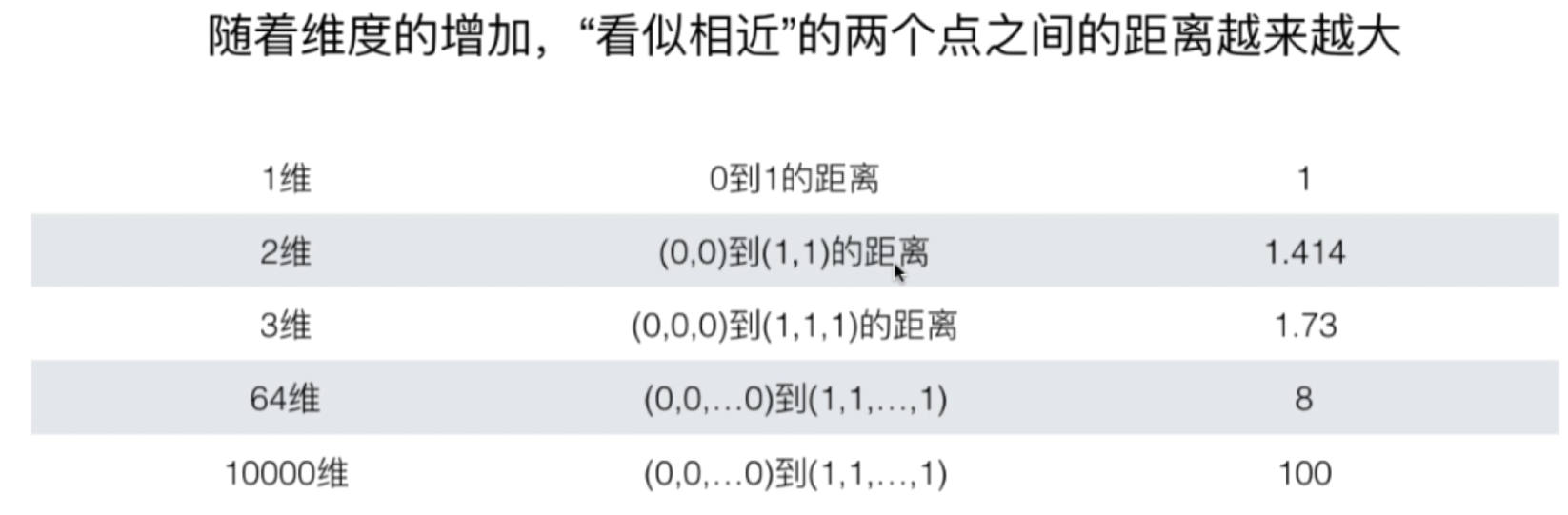
线性回归

作用

1.解决回归问题

2.思想简单，实现容易

3.许多强大的非线性模型的基础

4.结果具有很好的可解释性

5.蕴含机器学习中的很多重要思想

简单线性回归

import numpy as np


class SimpleLinearRegression1:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0
        for x, y in zip(x_train, y_train):
            num += (x - x_mean) * (y - y_mean)
            d += (x - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x，返回x的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression1()"

# 计算参数
from playML.SimpleLinearRegression import SimpleLinearRegression1

reg1 = SimpleLinearRegression1()
reg1.fit(x, y)
x_predict = 6
reg1.predict(np.array([x_predict]))

reg1.a_ # 0.8
reg1.b_ # 0.39999999999999947

# 画图
y_hat1 = reg1.predict(x)
plt.scatter(x, y)
plt.plot(x, y_hat1, color='r')
plt.axis([0, 6, 0, 6])
plt.show()

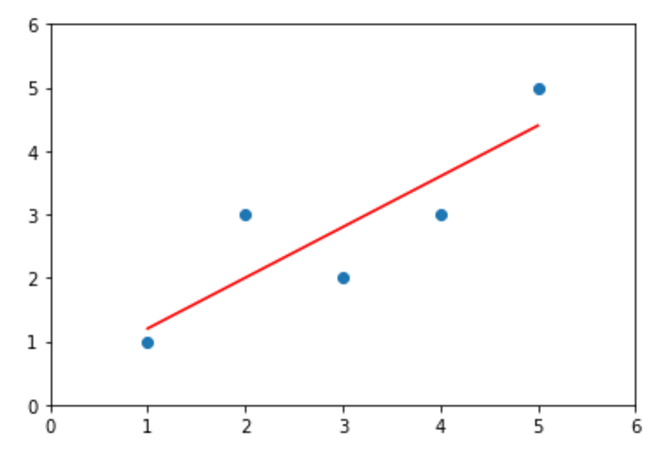
衡量线性回归法的指标

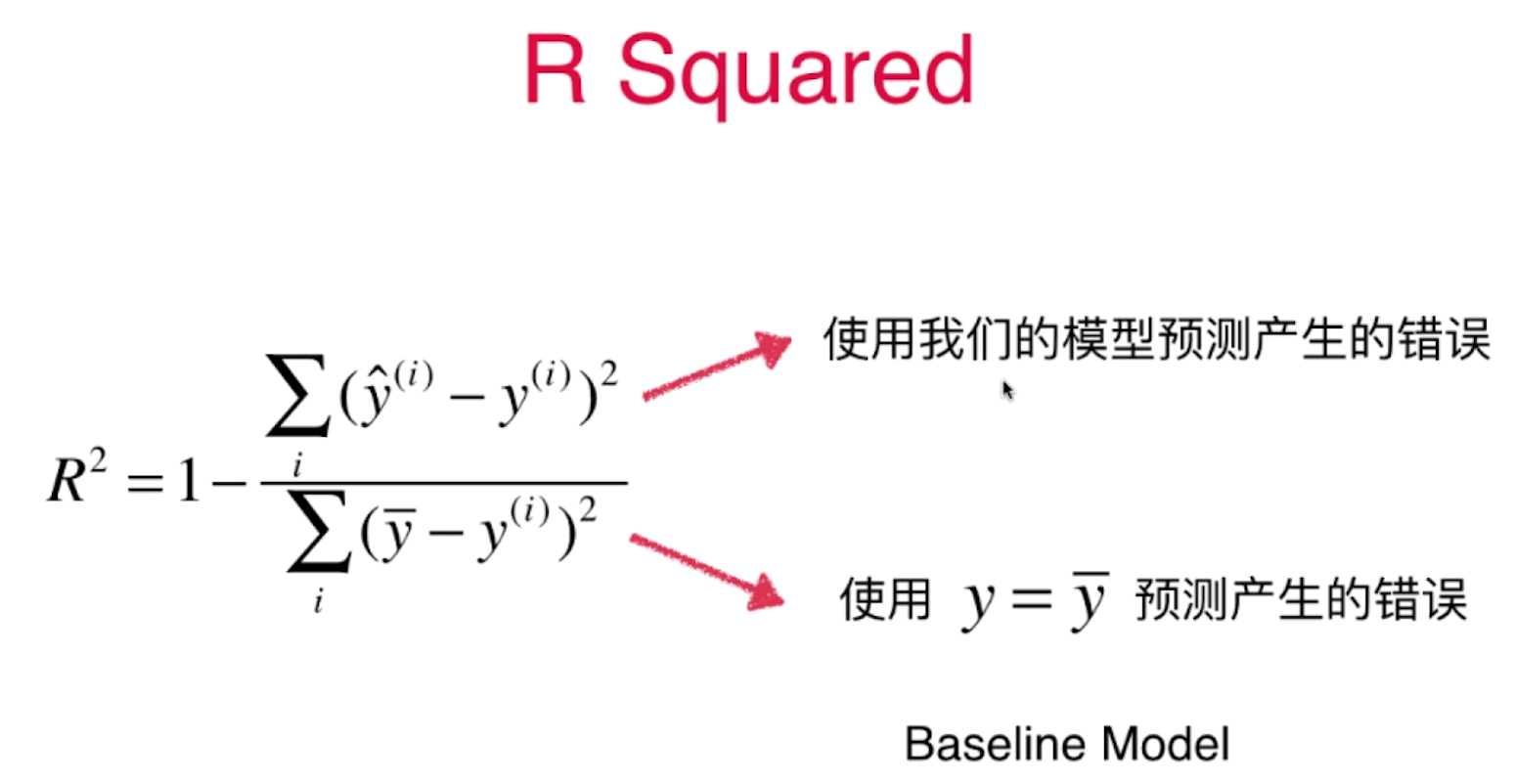
# 分割数据集
from playML.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, seed=666)

# 得到参数
from playML.SimpleLinearRegression import SimpleLinearRegression
reg = SimpleLinearRegression()
reg.fit(x_train, y_train)
reg.a_
reg.b_

# 精确度
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score

mean_squared_error(y_test, y_predict)  # 44.02437512559532
mean_absolute_error(y_test, y_predict)  # 4.219129679636869
r2_score(y_test, y_predict)  # 0.4027785009292951

多元线性回归

import numpy as np
from .metrics import r2_score


class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 数据加载
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]

# 数据分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

# 得到参数
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)  # LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

lin_reg.coef_  
# array([-1.14235739e-01,  3.12783163e-02, -4.30926281e-02, -9.16425531e-02,-1.09940036e+01,  3.49155727e+00,-1.40778005e-02, -1.06270960e+00,2.45307516e-01, -1.23179738e-02, -8.80618320e-01,  8.43243544e-03,-3.99667727e-01])

lin_reg.intercept_  # 32.64566083965309

# 打分
lin_reg.score(X_test, y_test)  # 0.8008916199519096


# 可解释性
# 系数越大，特征影响越明显
lin_reg.coef_  # array([-1.05574295e-01,  3.52748549e-02, -4.35179251e-02,  4.55405227e-01, -1.24268073e+01,  3.75411229e+00, -2.36116881e-02, -1.21088069e+00, 2.50740082e-01, -1.37702943e-02, -8.38888137e-01,  7.93577159e-03,-3.50952134e-01])

np.argsort(lin_reg.coef_)  # array([ 4,  7, 10, 12,  0,  2,  6,  9, 11,  1,  8,  3,  5], dtype=int64)

boston.feature_names[np.argsort(lin_reg.coef_)]    # array(['NOX', 'DIS', 'PTRATIO', 'LSTAT', 'CRIM', 'INDUS', 'AGE', 'TAX','B', 'ZN', 'RAD', 'CHAS', 'RM'], dtype='<U7')

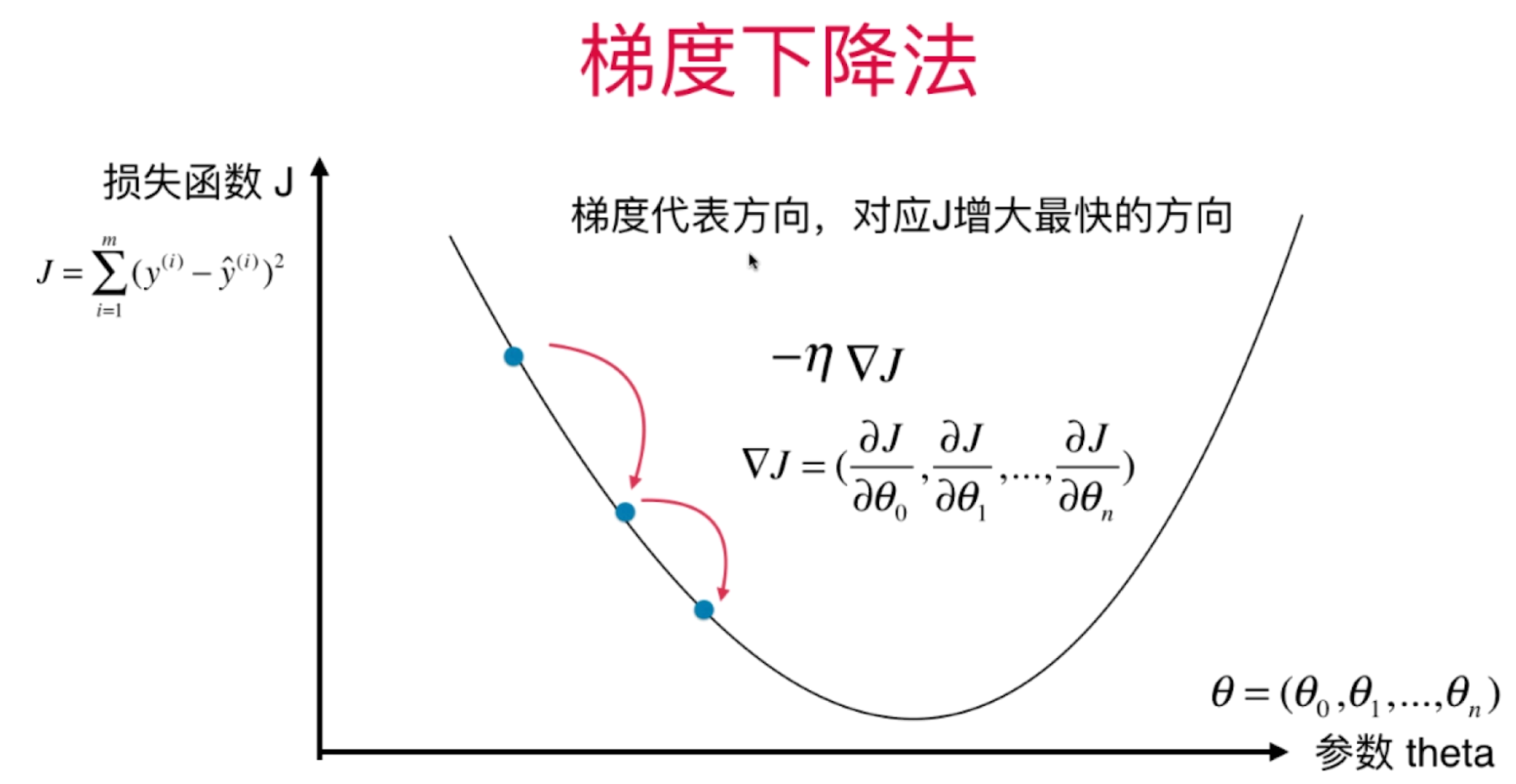
梯度下降

 理解：从向量的角度理解，梯度为导数向量的反方向，eta为取得的向量长度

 作用：得到一个函数后，如何求解？有时候并不可解，线性回归可以当作一个特例

 定义： 一步步逼近J最小值对应的theta。具体步骤：theta = theta - eta * gradient(导数大于0则theta变小，反之变大)。

参考文档 https://www.cnblogs.com/pinard/p/5970503.html

一元损失函数的梯度下降 

 

 

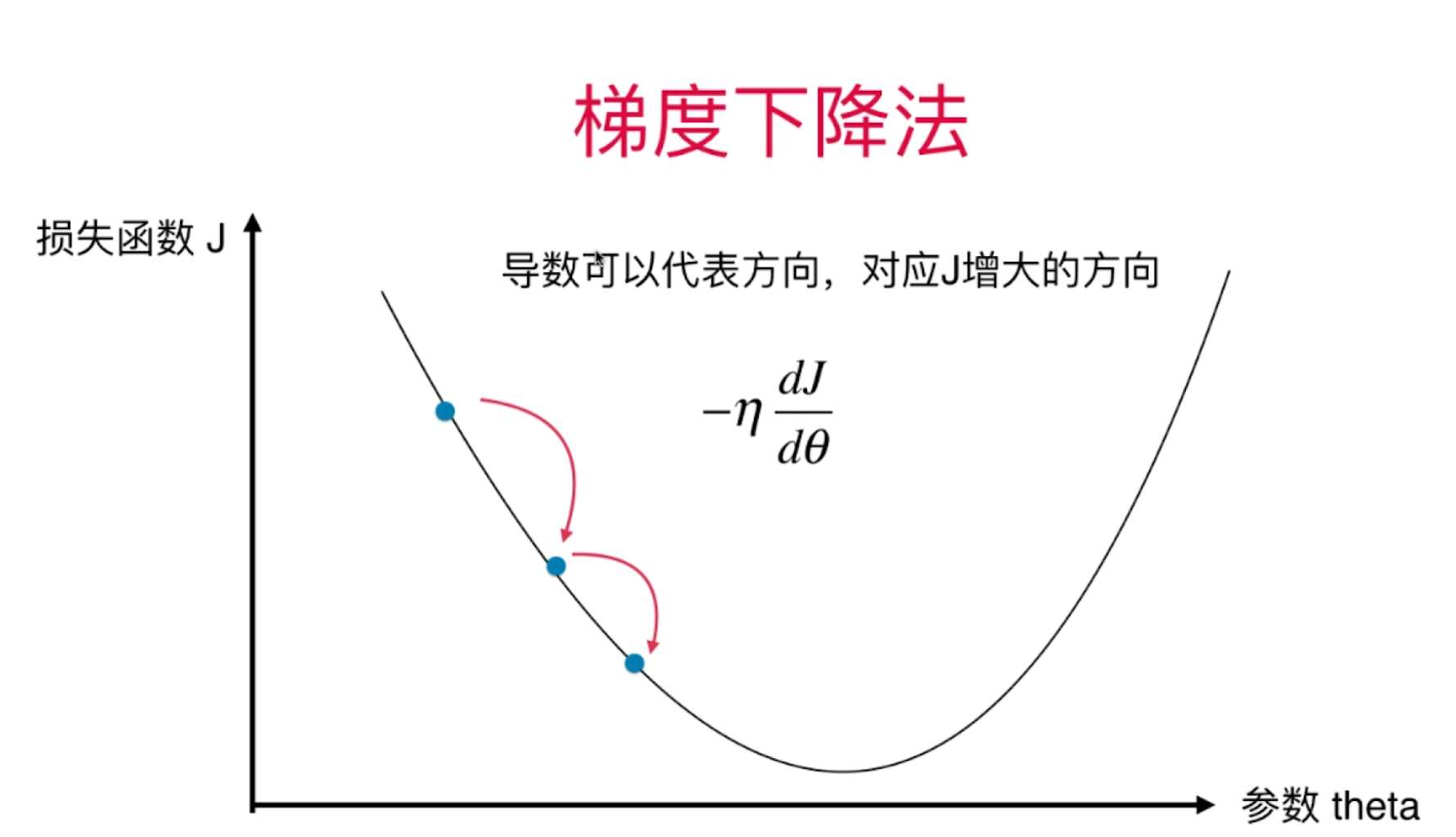
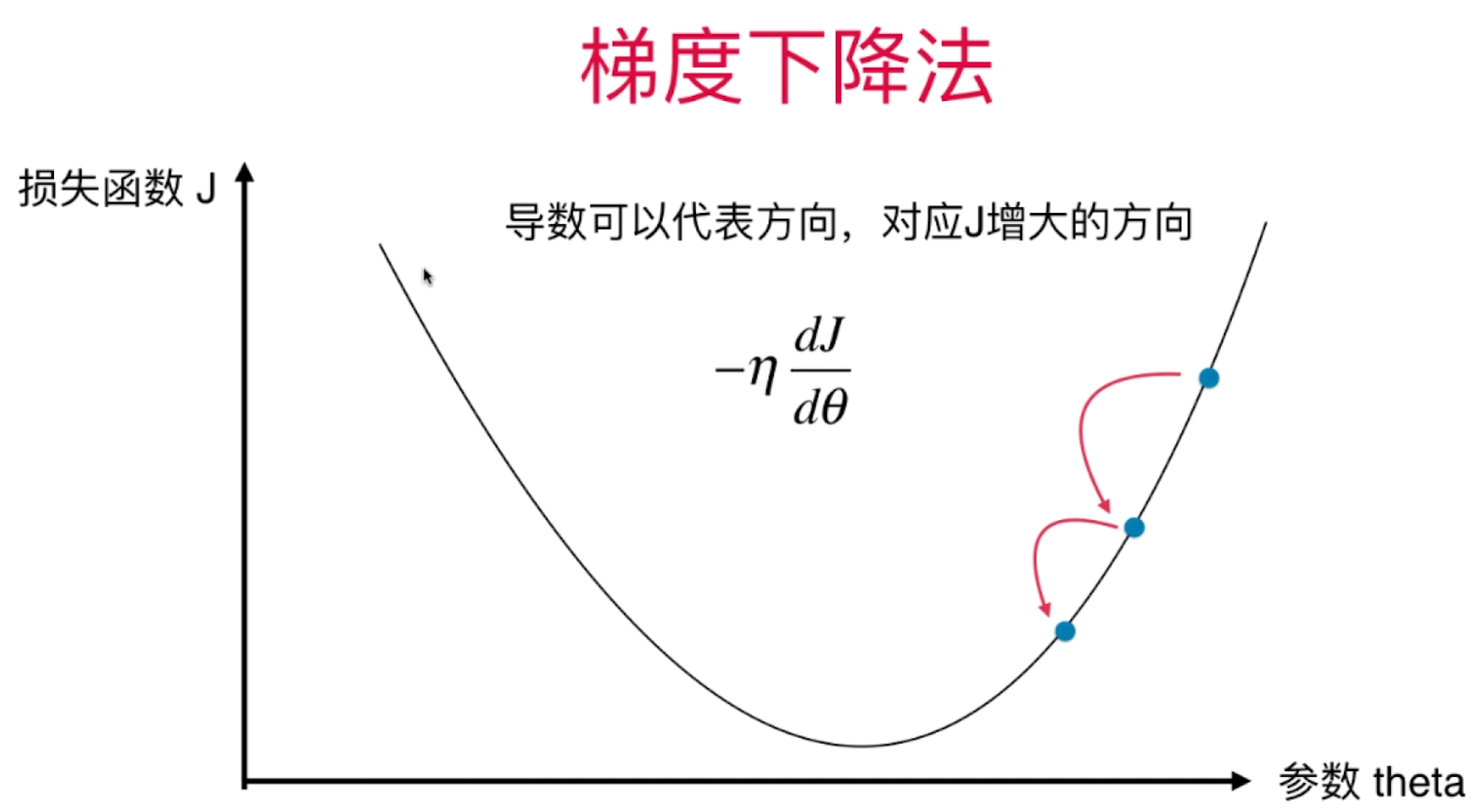
解释：dJ/d(theta)为导数的方向，-dJ/d(theta)为梯度的方向

 

epsilon = 1e-8
eta = 0.1

def J(theta):
    return (theta-2.5)**2 - 1.

def dJ(theta):
    return 2*(theta-2.5)

theta = 0.0
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta - eta * gradient
    
    if(abs(J(theta) - J(last_theta)) < epsilon):
        break
    
print(theta)  # print(theta)
print(J(theta))  # -0.99999998814289

theta = 0.0
theta_history = [theta]
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta - eta * gradient
    theta_history.append(theta)
    
    if(abs(J(theta) - J(last_theta)) < epsilon):
        break

plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r", marker='+')
plt.show()

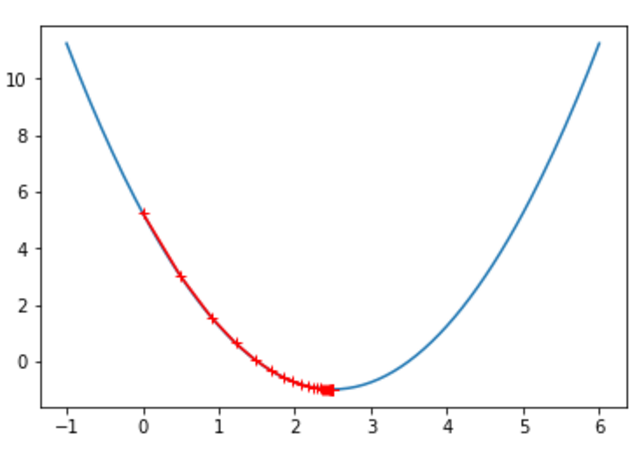
二元损失函数的梯度下降 

 

 

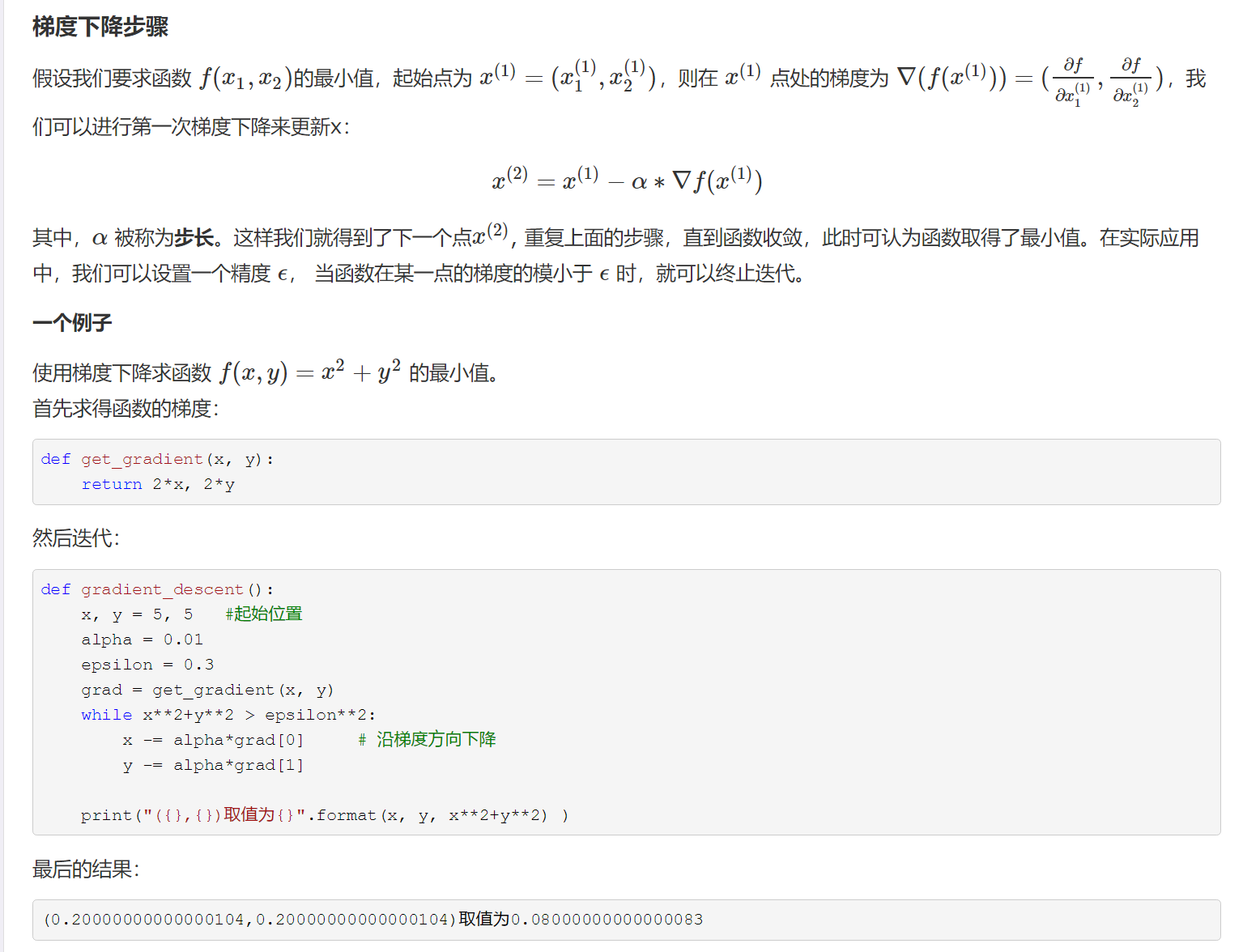
线性回归的梯度下降 

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            res = np.empty(len(theta))
            res[0] = np.sum(X_b.dot(theta) - y)
            for i in range(1, len(theta)):
                res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            return res * 2 / len(X_b)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = 2 * np.random.random(size=100)
y = x * 3. + 4. + np.random.normal(size=100)


from playML.LinearRegression import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit_gd(X, y)

lin_reg.coef_  # array([3.00706277])
lin_reg.intercept_  # 4.021457858204859

随机梯度下降　　

import numpy as np
from sklearn import datasets

# 加载数据集
boston = datasets.load_boston()
X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

# 拆分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)


# 数据集归一化
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)

# 预测
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor()
%time sgd_reg.fit(X_train_standard, y_train)  # Wall time: 74.2 ms
sgd_reg.score(X_test_standard, y_test)  #  0.8032705751514356

sgd_reg = SGDRegressor(n_iter=50)
%time sgd_reg.fit(X_train_standard, y_train)  # Wall time: 4.88 ms
sgd_reg.score(X_test_standard, y_test)  # 0.8129892326446553

总结

 梯度下降有3种算法：BGD、SGD、MGD

BGD全而慢，MGD小而快，MGD是折中选择

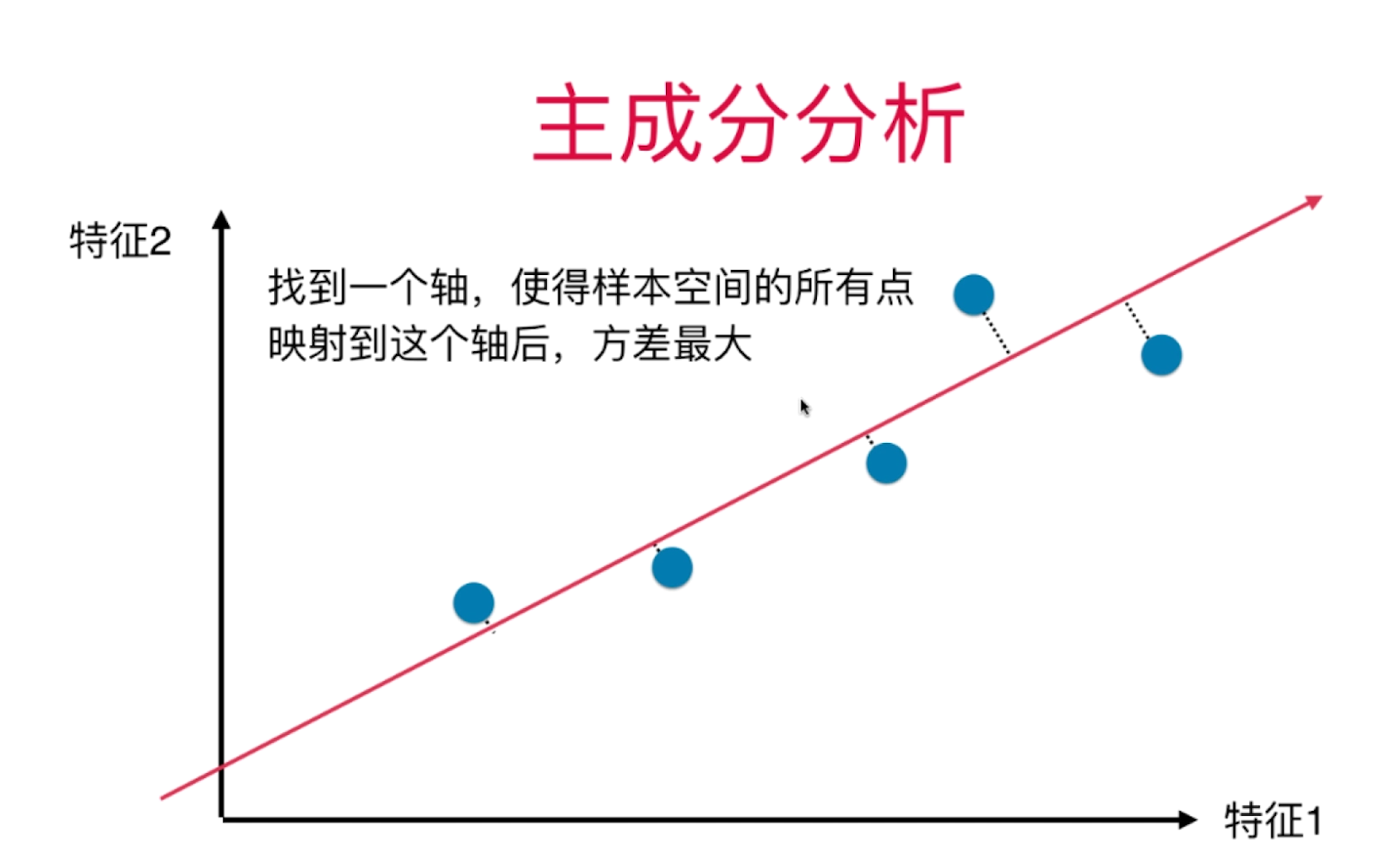
PCA