【运动传感器】Madgwick算法(上)
【运动传感器】Madgwick算法(上)
Madgwick算法能够综合多种传感器参数得到传感器的姿态。传感器可以采用以下两种配置:
- IMU:包含三轴线加速度计,测量物体坐标系下的三轴线加速度;三轴角速度计,测量物体坐标系下的三轴欧拉角变化率。1. MARG或AHRS:除了前述两类,还包含三轴磁力计,测量地球磁力线在物体坐标系下投影。 以下从原始传感器参数逐步推导出物体姿态。在推导过程中,大量使用四元数(quaternion)来表示旋转和姿态,不熟悉的同学可以参看这篇文章。
本文分上下两篇,上篇讲解各个传感器独立结果,下篇讲解融合方法、对误差的处理,以及标定实验。
本篇公式较多,可以直接关注各分段结尾处的“结论”。
欧拉角变化率和角速度(gyro
→
ω
\to \omega
→ω)
问题:已知欧拉角变化率,求角速度。
二维空间中的角速度
ω
\omega
ω是一个伪标量(pseudoscale)。其大小为单位时间转动过的弧度,其方向垂直于所在平面符合,和旋转方向符合右手定则,换言之,其方向为旋转轴。<br> 三维空间中的角速度
ω
\omega
ω是一个伪矢量(pseudovector),其大小为单位时间转动过的弧度,其方向和旋转方向符合右手定则。<br> <img src="https://img-blog.csdnimg.cn/img_convert/78c773c190e653396cfe7f7238e84eef.png" alt="这里写图片描述">
用矢量表示角速度时,可以直接使用矢量加法表示角速度的叠加。
绕
x
x
x轴旋转的角速度为
ω
x
i
\omega_x i
ωxi,其中
i
i
i表示旋转轴
[
1
,
0
,
0
]
[1,0,0]
[1,0,0];类似地,绕
y
,
z
y,z
y,z轴旋转的角速度为$ \omega_y j,\omega_z k $。
总体角速度和欧拉角变化率具有以下关系:
ω
=
ω
x
i
+
ω
y
j
+
ω
z
k
\omega = \omega_x i + \omega_y j+\omega_z k
ω=ωxi+ωyj+ωzk
其中,
i
,
j
,
k
i,j,k
i,j,k为三个轴单位矢量。
完整的证明较为繁琐,可以定性地考察一下这个结论。
考虑绕
x
x
x轴的旋转,该旋转发生在
y
z
yz
yz平面内,旋转矢量和
y
z
yz
yz平面垂直,即和
x
x
x轴平行。<br>
ω
\omega
ω在
x
x
x轴投影为
ω
x
\omega_x
ωx,就是绕
x
x
x轴的旋转速度。</p>
角速度
ω
\omega
ω的旋转轴(归一化长度)为:<br>
[
ω
x
,
ω
y
,
ω
z
]
ω
x
2
+
ω
y
2
+
ω
z
2
\frac{[\omega_x,\omega_y,\omega_z]}{\sqrt {\omega_x^2+\omega_y^2+\omega_z^2} }
ωx2+ωy2+ωz2
<svg width="400em" height="1.8800000000000001em" viewbox="0 0 400000 1944" preserveaspectratio="xMinYMin slice">
<path d="M1001,80H400000v40H1013.1s-83.4,268,-264.1,840c-180.7,
572,-277,876.3,-289,913c-4.7,4.7,-12.7,7,-24,7s-12,0,-12,0c-1.3,-3.3,-3.7,-11.7, -7,-25c-35.3,-125.3,-106.7,-373.3,-214,-744c-10,12,-21,25,-33,39s-32,39,-32,39 c-6,-5.3,-15,-14,-27,-26s25,-30,25,-30c26.7,-32.7,52,-63,76,-91s52,-60,52,-60 s208,722,208,722c56,-175.3,126.3,-397.3,211,-666c84.7,-268.7,153.8,-488.2,207.5, -658.5c53.7,-170.3,84.5,-266.8,92.5,-289.5c4,-6.7,10,-10,18,-10z M1001 80H400000v40H1013z"></path> </svg>[ωx,ωy,ωz]
旋转速度(单位时间旋转的角度)为:
ω
x
2
+
ω
y
2
+
ω
z
2
\sqrt {\omega_x^2+\omega_y^2+\omega_z^2}
ωx2+ωy2+ωz2
<svg width="400em" height="1.8800000000000001em" viewbox="0 0 400000 1944" preserveaspectratio="xMinYMin slice">
<path d="M1001,80H400000v40H1013.1s-83.4,268,-264.1,840c-180.7,
572,-277,876.3,-289,913c-4.7,4.7,-12.7,7,-24,7s-12,0,-12,0c-1.3,-3.3,-3.7,-11.7, -7,-25c-35.3,-125.3,-106.7,-373.3,-214,-744c-10,12,-21,25,-33,39s-32,39,-32,39 c-6,-5.3,-15,-14,-27,-26s25,-30,25,-30c26.7,-32.7,52,-63,76,-91s52,-60,52,-60 s208,722,208,722c56,-175.3,126.3,-397.3,211,-666c84.7,-268.7,153.8,-488.2,207.5, -658.5c53.7,-170.3,84.5,-266.8,92.5,-289.5c4,-6.7,10,-10,18,-10z M1001 80H400000v40H1013z"></path> </svg>
此部分证明原文可以参看维基百科角速度词条。
结论:
ω
=
[
0
,
ω
x
,
ω
y
,
ω
z
]
\omega = [0, \omega_x, \omega_y ,\omega_z]
ω=[0,ωx,ωy,ωz]。</p>
角速度和姿态四元数(
ω
→
q
\omega \to q
ω→q)
问题:已知传感器坐标系下角速度和当前姿态四元数,求姿态四元数变化率,进而求姿态四元数。
首先考虑一个稍简单的情况,已知世界坐标系下角速度
ω
ˉ
\bar{\omega}
ωˉ,以及当前姿态四元数
q
q
q,求
q
˙
\dot{q}
q˙。(上标一点表示对时间的一次微分)。
考虑空间中任意一点
R
0
=
[
0
,
x
0
,
y
0
,
z
0
]
R_0=[0,x_0,y_0,z_0]
R0=[0,x0,y0,z0],当前时刻的位置为
R
t
R_t
Rt,以下通过两个方面来写出当前线速度
R
t
˙
\dot{R_t}
Rt˙的表达。
第一方面,由于
R
t
R_t
Rt是
R
0
R_0
R0经过变换
q
q
q得到的,故:<br>
R
t
=
q
×
R
0
×
q
−
1
(
1
)
R_t = q\times R_0 \times q^{-1}\ \ \ \ \ \ \ \ \ (1)
Rt=q×R0×q−1 (1)
对时间
t
t
t求导,注意只有
q
q
q是
t
t
t的函数,
R
0
R_0
R0常量:<br>
R
t
˙
=
q
˙
×
R
0
×
q
−
1
+
q
×
R
0
×
q
−
1
˙
(
2
)
\dot{R_t} = \dot{q}\times R_0 \times q^{-1} + q \times R_0 \times \dot{q^{-1}}\ \ \ \ \ \ \ \ \ (2)
Rt˙=q˙×R0×q−1+q×R0×q−1˙ (2)
根据式(1)(此处存疑,叉乘不满足结合律?),有:
q
−
1
×
R
t
=
R
0
×
q
−
1
q^{-1}\times R_t = R_0 \times q^{-1}
q−1×Rt=R0×q−1
R
t
×
q
=
q
×
R
0
R_t \times q = q \times R_0
Rt×q=q×R0
代入式(2):
R
t
˙
=
q
˙
×
q
−
1
×
R
t
+
R
t
×
q
×
q
−
1
˙
(
3
)
\dot{R_t} = \dot{q}\times q^{-1}\times R_t + R_t\times q\times \dot{q^{-1}}\ \ \ \ \ \ \ \ \ (3)
Rt˙=q˙×q−1×Rt+Rt×q×q−1˙ (3)
考察
q
q
q和其反变换
q
−
1
q^{-1}
q−1的叉乘:<br>
q
×
q
−
1
=
[
q
0
,
q
1
,
q
2
,
q
3
]
×
[
q
0
,
−
q
1
,
−
q
2
,
−
q
3
]
=
[
q
0
2
+
q
1
2
+
q
2
2
+
q
3
2
,
0
,
0
,
0
]
=
[
1
,
0
,
0
,
0
]
q\times q^{-1} = [q_0,q_1,q_2,q_3]\times[q_0,-q_1,-q_2,-q_3] = [q_0^2+q_1^2+q_2^2+q_3^2,0,0,0] = [1,0,0,0]
q×q−1=[q0,q1,q2,q3]×[q0,−q1,−q2,−q3]=[q02+q12+q22+q32,0,0,0]=[1,0,0,0]
叉乘结果是个常数矢量,所以其对于时间的导数是0:
q
˙
×
q
−
1
+
q
×
q
−
1
˙
=
0
\dot{q}\times q^{-1}+q\times \dot{q^{-1}}=0
q˙×q−1+q×q−1˙=0<br>
q
˙
×
q
−
1
=
−
q
×
q
−
1
˙
\dot{q}\times q^{-1}=-q\times \dot{q^{-1}}
q˙×q−1=−q×q−1˙
把此结果代入式(3):
R
t
˙
=
q
˙
×
q
−
1
×
R
t
−
R
t
×
q
˙
×
q
−
1
(
3
)
\dot{R_t} = \dot{q}\times q^{-1}\times R_t - R_t\times \dot{q} \times q^{-1}\ \ \ \ \ \ \ \ \ (3)
Rt˙=q˙×q−1×Rt−Rt×q˙×q−1 (3)
考察
q
˙
×
q
−
1
\dot{q}\times q^{-1}
q˙×q−1的标量部分(即四元数第一分量):<br>
S
c
a
l
e
(
q
˙
×
q
−
1
)
=
q
0
˙
q
0
+
q
1
˙
q
1
+
q
2
˙
q
2
+
q
3
˙
q
3
=
1
2
d
d
t
(
q
0
2
+
q
1
2
+
q
2
2
+
q
3
2
)
=
0
Scale(\dot{q}\times q^{-1}) = \dot{q_0}q_0+\dot{q_1}q_1+\dot{q_2}q_2+\dot{q_3}q_3=\frac{1}{2}\frac{d}{dt}(q_0^2+q_1^2+q_2^2+q_3^2)=0
Scale(q˙×q−1)=q0˙q0+q1˙q1+q2˙q2+q3˙q3=21dtd(q02+q12+q22+q32)=0<br> 说明
q
˙
×
q
−
1
\dot{q}\times q^{-1}
q˙×q−1是一个纯矢量。由于矢量叉乘满足反交换律:
a
×
b
=
−
b
×
a
a\times b = -b\times a
a×b=−b×a。(3)式变成:
R
t
˙
=
2
q
˙
×
q
−
1
×
R
t
\dot{R_t} = 2 \dot{q}\times q^{-1}\times R_t
Rt˙=2q˙×q−1×Rt
回顾:四元数
q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
q=q_0+q_1i+q_2j+q_3k
q=q0+q1i+q2j+q3k。由一个标量
q
0
q_0
q0,和一个矢量
q
1
i
+
q
2
j
+
q
3
k
q_1i+q_2j+q_3k
q1i+q2j+q3k组成。</p>
第二方面,线速度= 角速度
×
\times
×弧长:<br>
R
t
˙
=
ω
ˉ
×
R
t
\dot{R_t} = \bar{\omega} \times R_t
Rt˙=ωˉ×Rt
综合第一、第二方面的结论,要想让两式对于任意
R
0
R_0
R0都相等,有:
2
q
˙
×
q
−
1
=
ω
ˉ
→
q
˙
=
1
2
ω
ˉ
×
q
(
4
)
2 \dot{q}\times q^{-1} = \bar{\omega} \to \dot{q} = \frac{1}{2}\bar{\omega} \times q \ \ \ \ \ \ \ \ \ \ \ (4)
2q˙×q−1=ωˉ→q˙=21ωˉ×q (4)
注意此处
ω
ˉ
\bar{\omega}
ωˉ表示**世界坐标系**下的角速度。它可以通过**传感器坐标系**下角速度
ω
\omega
ω经过变换
q
q
q得到:
ω
ˉ
=
q
×
ω
×
q
−
1
\bar{\omega} = q\times \omega \times q^{-1}
ωˉ=q×ω×q−1
引理:将原始坐标系A施加变换
q
q
q获得坐标系B。则对于同一点,A到B的坐标变换为
q
−
1
q^{-1}
q−1。<br> 证明:为书写简便,用矩阵相乘形式表示变换,例如
q
∙
x
A
q \bullet x_A
q∙xA。<br> 设有两个点
x
,
y
x,y
x,y,他们在两个坐标系中的坐标相同:
x
A
=
y
B
x_A = y_B
xA=yB。 由于两点相对各自坐标系位置相同,可以认为
y
y
y是
x
x
x经过变换
q
q
q得到的:<br>
y
A
=
q
∙
x
A
y_A = q \bullet x_A
yA=q∙xA</p>
这个变换结果是在A坐标系下,设A到B的坐标变换矩阵为 q ∗ q^* q∗:
q ∗ ∙ y A = q ∗ ∙ q ∙ x A = y B q^*\bullet y_A = q^*\bullet q\bullet x_A = y_B q∗∙yA=q∗∙q∙xA=yB
所以得到坐标变换矩阵: q ∗ = q − 1 q^*=q^{-1} q∗=q−1
代入(4)式,得到:
2
q
˙
×
q
−
1
=
ω
ˉ
→
q
˙
=
1
2
q
×
ω
2 \dot{q}\times q^{-1} = \bar{\omega} \to \dot{q} = \frac{1}{2}q \times \omega
2q˙×q−1=ωˉ→q˙=21q×ω
此部分证明原文可以参看euclideanspace网站。
进一步,可以得到一段时间内四元数的变换:
q
t
=
q
t
−
1
+
q
˙
Δ
t
q_t = q_{t-1} + \dot{q} \Delta t
qt=qt−1+q˙Δt
结论:
q
t
=
q
t
−
1
+
1
2
q
t
×
ω
t
Δ
t
q_t = q_{t-1} + \frac{1}{2}q_t \times \omega_t \Delta t
qt=qt−1+21qt×ωtΔt</p>
加速度计、磁力计和姿态四元数(acce, mag
→
q
\to q
→q)
问题:已知加速度计、磁力计读数,求姿态四元数。
重力矢量和磁场矢量在世界坐标系下的三个分量根据物理常识已知。 磁力计测量磁场矢量在传感器坐标系下的三个分量。
设
d
E
=
[
0
,
d
e
x
,
d
e
y
,
d
e
z
]
d_E=[0,de_x,de_y,de_z]
dE=[0,dex,dey,dez]为世界坐标系下的矢量坐标。设
q
q
q为传感器姿态。根据前节引理,使用
q
−
1
q^{-1}
q−1可以把
d
E
d_E
dE变换为传感器坐标系下的矢量坐标
d
S
=
[
0
,
d
s
x
,
d
s
y
,
d
s
z
]
d_S=[0,ds_x,ds_y,ds_z]
dS=[0,dsx,dsy,dsz]:
d
S
=
q
−
1
×
d
E
×
q
d_S = q^{-1}\times d_E \times q
dS=q−1×dE×q
满足这个方程的解不唯一。设
q
q
q为方程的一个解,考虑一个以
d
E
d_E
dE为轴的旋转
Δ
q
\Delta q
Δq。两者的复合变换为
Δ
q
×
q
\Delta q\times q
Δq×q。<br>
(
Δ
q
×
q
)
−
1
×
d
E
×
(
Δ
q
×
q
)
=
q
−
1
×
(
Δ
q
−
1
×
d
E
×
Δ
q
)
×
q
(\Delta q \times q)^{-1}\times d_E \times (\Delta q \times q) = q^{-1} \times (\Delta q^{-1}\times d_E \times \Delta q) \times q
(Δq×q)−1×dE×(Δq×q)=q−1×(Δq−1×dE×Δq)×q
向量绕自身旋转不会发生变化,所以括号内部分等于
d
E
d_E
dE,上式仍然等于
d
S
d_S
dS。即:**绕轴的旋转不会改变传感器的示数**。
为了获得一个确定的解,需要从优化的角度来求解。找到
q
q
q,最小化以下标量误差:
f
(
q
)
=
∣
∣
q
−
1
×
d
E
×
q
−
d
S
∣
∣
2
=
e
(
q
)
T
e
(
q
)
f(q) = || q^{-1}\times d_E \times q - d_S ||^2 = e(q)^T e(q)
f(q)=∣∣q−1×dE×q−dS∣∣2=e(q)Te(q)
使用高斯牛顿法求解:
q
k
+
1
=
q
k
−
μ
∇
f
∣
∣
∇
f
∣
∣
q_{k+1}=q_k - \mu \frac{\nabla f}{||\nabla f||}
qk+1=qk−μ∣∣∇f∣∣∇f
其中
μ
\mu
μ为步长,
∇
\nabla
∇为微分算子,表示标量
f
f
f对于矢量
q
q
q的变化率。其和误差矢量
e
(
q
)
e(q)
e(q)的关系如下:
∇
f
(
q
)
=
J
(
q
)
e
(
q
)
\nabla f(q) = J(q) e(q)
∇f(q)=J(q)e(q)
其中
e
(
q
)
e(q)
e(q)尺寸为
4
×
1
4\times 1
4×1。
J
(
q
)
J(q)
J(q)尺寸为
4
×
4
4\times 4
4×4,
J
i
j
=
∂
(
e
i
)
/
∂
q
j
J_{ij} = \partial(e_i)/\partial q_j
Jij=∂(ei)/∂qj。都可以写出解析表达式。
为节约时间,每个采样间隔只进行一次迭代:
q
t
+
1
=
q
t
−
μ
t
∇
f
∣
∣
∇
f
∣
∣
q_{t+1}=q_t - \mu_t \frac{\nabla f}{||\nabla f||}
qt+1=qt−μt∣∣∇f∣∣∇f
其中步长和当前时刻误差项的二阶导有关,
α
\alpha
α为固定参数,
Δ
t
\Delta_t
Δt为采样间隔:
μ
t
=
α
∣
∣
q
˙
∣
∣
Δ
t
\mu_t = \alpha ||\dot{q}||\Delta_t
μt=α∣∣q˙∣∣Δt
采样间隔越大,变化速率越快,步长应该越大。
加速度计
d
E
=
[
0
,
0
,
0
,
1
]
d_E = [0,0,0,1]
dE=[0,0,0,1],
d
S
=
[
0
,
a
x
,
a
y
,
a
z
]
d_S=[0,a_x,a_y,a_z]
dS=[0,ax,ay,az]。有:<br>
e
(
q
)
=
[
2
(
q
1
q
3
−
q
0
q
2
)
−
a
x
2
(
q
0
q
1
+
q
2
q
3
)
−
a
y
2
(
1
2
−
q
1
2
−
q
2
2
)
−
a
z
]
T
e(q)=\begin{bmatrix} 2(q_1q_3 - q_0q_2)-a_x & 2(q_0q_1+q_2q_3)-a_y & 2(\frac{1}{2}-q_1^2-q_2^2)-a_z\end{bmatrix}^T
e(q)=[2(q1q3−q0q2)−ax2(q0q1+q2q3)−ay2(21−q12−q22)−az]T
J
(
q
)
=
[
−
2
q
2
2
q
3
−
2
q
0
2
q
1
2
q
1
2
q
0
2
q
3
2
q
2
0
−
4
q
1
−
4
q
2
0
]
J(q) = \begin{bmatrix} -2q_2 & 2q_3 & -2q_0 & 2q_1 \\ 2q_1 & 2q_0 & 2q_3 & 2q_2 \\ 0 & -4q_1 & -4q_2 & 0 \end{bmatrix}
J(q)=⎣⎡−2q22q102q32q0−4q1−2q02q3−4q22q12q20⎦⎤
为书写简便,省去了
e
,
J
e,J
e,J中为0的部分。<br> 使用加速度计估计的姿态只在加速度为0条件下准确。但后续融合算法中,加速度计和磁力计只起到修正的作用,影响不大。
磁力计
粗略来说,地球磁力线处于经线和垂直轴构成的平面内,在东西方向投影为0。磁力线大小(Intensity)和方向(Inclination)随地理位置变化,在两极最大,赤道最小;在北极为90°(朝下),在赤道为0°,在南极为-90°(朝上)。具体数值可以根据当地经纬度查询维基百科。
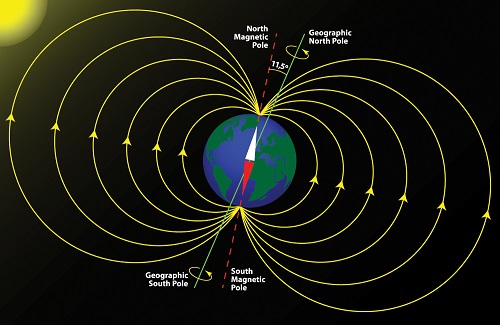
不失一般性地,设
d
E
=
[
0
,
b
x
,
0
,
b
z
]
d_E=[0,b_x,0,b_z]
dE=[0,bx,0,bz],
d
S
=
[
0
,
m
x
,
m
y
,
m
z
]
d_S=[0,m_x,m_y,m_z]
dS=[0,mx,my,mz]。
e
(
q
)
1
=
2
b
x
(
0.5
−
q
2
2
−
q
3
2
)
+
2
b
z
(
q
1
q
3
−
q
0
q
2
)
−
m
x
e(q)_1=2b_x(0.5-q_2^2-q_3^2)+2b_z(q_1q_3-q_0q_2)-m_x
e(q)1=2bx(0.5−q22−q32)+2bz(q1q3−q0q2)−mx
e
(
q
)
2
=
2
b
x
(
q
1
q
2
−
q
0
q
3
)
+
2
b
z
(
q
0
q
1
+
q
2
q
3
)
−
m
y
e(q)_2=2b_x(q_1q_2-q_0q_3)+2b_z(q_0q_1+q_2q_3)-m_y
e(q)2=2bx(q1q2−q0q3)+2bz(q0q1+q2q3)−my
e
(
q
)
3
=
2
b
x
(
q
0
q
2
+
q
1
q
3
)
+
2
b
z
(
0.5
−
q
1
2
−
q
2
2
)
−
m
z
e(q)_3=2b_x(q_0q_2+q_1q_3)+2b_z(0.5-q_1^2-q_2^2)-m_z
e(q)3=2bx(q0q2+q1q3)+2bz(0.5−q12−q22)−mz
J
(
q
)
=
[
−
2
b
z
q
2
2
b
z
q
3
−
4
b
x
q
2
−
2
b
z
q
0
−
4
b
x
q
3
+
2
b
z
q
1
−
2
b
x
q
3
+
2
b
z
q
1
2
b
x
q
2
+
2
b
z
q
0
2
b
x
q
1
+
2
b
z
q
3
−
2
b
x
q
0
+
2
b
z
q
2
2
b
x
q
2
2
b
x
q
3
−
4
b
z
q
1
2
b
x
q
0
−
4
b
z
q
2
2
b
x
q
1
]
J(q)=\begin{bmatrix} -2b_zq_2 & 2b_zq_3 & -4b_xq_2-2b_zq_0 & -4b_xq_3+2b_zq_1\\ -2b_xq_3+2b_zq_1 & 2b_xq_2+2b_zq_0 & 2b_xq_1+2b_zq_3 & -2b_xq_0+2b_zq_2\\ 2b_xq_2 & 2b_xq_3-4b_zq_1 & 2b_xq_0-4b_zq_2 & 2b_xq_1\end{bmatrix}
J(q)=⎣⎡−2bzq2−2bxq3+2bzq12bxq22bzq32bxq2+2bzq02bxq3−4bzq1−4bxq2−2bzq02bxq1+2bzq32bxq0−4bzq2−4bxq3+2bzq1−2bxq0+2bzq22bxq1⎦⎤
这部分证明原文参看Madgwick内部报告。
结论:
q
t
+
1
=
q
t
−
μ
t
J
(
q
)
e
(
q
)
∣
∣
J
(
q
)
e
(
q
)
∣
∣
q_{t+1}=q_t - \mu_t \frac{J(q)e(q)}{||J(q)e(q)||}
qt+1=qt−μt∣∣J(q)e(q)∣∣J(q)e(q)</p>
至此,使用角速度计、加速度计、磁力计可以分别计算出当前姿态。在下篇中,会介绍它们的融合方法,对误差的处理,以及标定实验。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号