蒙特卡洛-马尔科夫链(MCMC)的混合速度
蒙特卡洛-马尔科夫链(MCMC)的混合速度
在应用Markov Chain Monte Carlo的文章中,常常遇到这样的说法:“马氏链的混合速度”,“某马氏链混合很慢”,“转移概率严重尖峰(peaked)”。本文用简单的例子讲解这一概念。
MCMC的初步理解可以参看这篇博客。
马氏链的平稳态
符合一定条件的马氏链能够收敛到一个平稳态。换言之,给定随机变量的条件分布(概率转移矩阵),马氏链中的样本最终会达到其先验分布(平稳态)。这里不做数学推导,仅给出一个直观的例子。
例子:平稳态
有一个学生每天考试,如果考得不好记为
x
=
0
x=0
x=0,考得好记为
x
=
1
x=1
x=1。我们不知道他考好考坏的概率
p
(
x
)
p(x)
p(x),但是通过调查可以知道相邻两天成绩的条件概率/状态转移矩阵
T
:
T
i
j
=
P
(
j
→
i
)
T:T_{ij}=P(j \to i)
T:Tij=P(j→i):
| . | x t = 0 x_{t}=0 xt=0 | x t = 1 x_{t}=1 xt=1 |
|---|---|---|
| x t + 1 = 0 x_{t+1}=0 xt+1=0 | T 00 = 0.70 T_{00}=0.70 T00=0.70 | T 01 = 0.05 T_{01}=0.05 T01=0.05 |
| x t + 1 = 1 x_{t+1}=1 xt+1=1 | T 10 = 0.30 T_{10}=0.30 T10=0.30 | T 11 = 0.95 T_{11}=0.95 T11=0.95 |
已知其第一天的考试成绩(
p
0
=
[
0
;
1
]
或
者
p
0
=
[
1
;
0
]
p_0=[0;1]或者p_0=[1;0]
p0=[0;1]或者p0=[1;0]),第N天的考试成绩的概率分布为<br>
p
N
=
∏
i
=
1
N
T
⋅
p
0
p_N = \prod_{i=1}^N T \cdot p_0
pN=i=1∏NT⋅p0
考不好有30%机会翻盘,考得好则有95%机会保持胜利,证明总体考好的机会很大。可以看到,无论第一天成绩如何,在大约12天后,考好的概率都收敛到大约0.8以上。换言之,到了第12天,这位同学就“忘记”了第一天的成绩,此时的概率就是这个马氏链的平稳态
p
(
x
=
1
)
p(x=1)
p(x=1)。<br> <img src="https://img-blog.csdnimg.cn/img_convert/768c926d516a0fa62094ec6299ee90a1.png" alt="这里写图片描述">
马氏链的混合速度
马尔科夫链-蒙特卡洛实际是一种近似的蒙特卡洛算法。真正的蒙特卡洛算法应该使用相互独立的一系列采样来逼近待求结果;而马尔科夫链-蒙特卡洛的一系列采样来自一个马氏链,每两个相邻的样本之间相关。 从转移函数的角度来说,希望
Q
(
x
t
+
1
∣
x
t
)
Q(x_{t+1}|x_t)
Q(xt+1∣xt)尽量平滑,尽量靠近均匀分布,不要有强烈的尖峰(peak)。从信息量的角度来说,希望
x
t
+
1
x_{t+1}
xt+1相对于
x
t
x_t
xt尽量独立,
x
t
x_t
xt。
例子:混合速度
依然是上述考试例子。考虑另一个学生,
p
(
0
→
1
)
=
0.45
p(0 \to 1)=0.45
p(0→1)=0.45,
p
(
1
→
0
)
=
0.4
p(1 \to 0) = 0.4
p(1→0)=0.4。这位同学心理包袱比较小,前一天对后一天的影响不大。
| . | x t = 0 x_{t}=0 xt=0 | x t = 1 x_{t}=1 xt=1 |
|---|---|---|
| x t + 1 = 0 x_{t+1}=0 xt+1=0 | T 00 = 0.55 T_{00}=0.55 T00=0.55 | T 01 = 0.4 T_{01}=0.4 T01=0.4 |
| x t + 1 = 1 x_{t+1}=1 xt+1=1 | T 10 = 0.45 T_{10}=0.45 T10=0.45 | T 11 = 0.6 T_{11}=0.6 T11=0.6 |
无论第一天考得怎样,第四天之后,考好的概率和第一天的成绩基本就无关了,也就是忘记了第一天的成绩。由于转移函数更“平滑”(更趋近均匀分布),前一天提供给后一天的信息量更小,马氏链混合得更快。
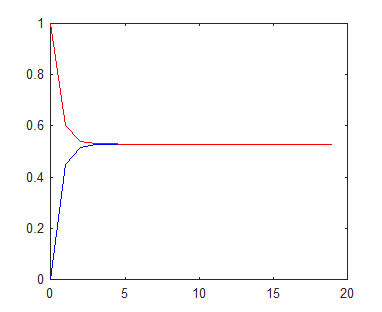
另两种极端情况:取反或者一锤子买卖
T
=
[
01
10
]
o
r
T
=
[
10
01
]
T= \left [ \begin{matrix} 0 1 \\ 1 0\end {matrix} \right ] or\ \ T= \left [ \begin{matrix} 1 0 \\ 0 1\end {matrix} \right ]
T=[0110]or T=[1001]
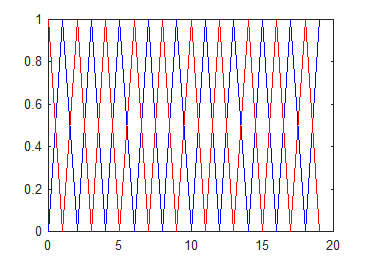
这两种情况都不会收敛。
构造混合更快的马氏链
很多时候,我们无法直接获得待求随机变量的条件转移概率
p
(
x
t
+
1
∣
x
t
)
p(x_{t+1}|x_t)
p(xt+1∣xt),而需要借助一个不需要求的隐变量
h
h
h,通过以下步骤求解马氏链的下一个采样:
p
(
h
∣
x
t
)
p(h|x_t)
p(h∣xt),采样
h
t
h_t
ht</li><li>根据
p
(
x
∣
h
t
)
p(x|h_t)
p(x∣ht),采样
x
t
+
1
x_{t+1}
xt+1<br> 在设定
h
h
h时,应该尽量选择和
x
x
x相关性弱的变量(weak dependent),使得两个条件概率更为平滑(not peaked)。<br> 以上述考试为例,如果选择“是否复习了”作为隐变量
h
h
h,则
x
,
h
x,h
x,h之间强相关。构造出的马氏链中
x
t
x_t
xt对
x
t
+
1
x_{t+1}
xt+1决定性很强,混合较慢。<br> 如果选择“是否洗澡了”作为
h
h
h,则
x
,
h
x,h
x,h之间相关性很弱,混合较快。这种情况下:<br>
p
(
x
∣
h
)
=
p
(
x
,
h
)
p
(
h
)
≈
p
(
x
)
⋅
p
(
h
)
p
(
h
)
=
p
(
x
)
p(x|h) = \frac{p(x,h)}{p(h)} \approx \frac{p(x)\cdot p(h)}{p(h)} = p(x)
p(x∣h)=p(h)p(x,h)≈p(h)p(x)⋅p(h)=p(x)</li>
由于洗澡和考试没啥关系,所以在调查“洗了澡能不能考好”的时候,实际就等价于调查“能不能考好”。
例子:reparameterization
考虑这样一个模型,包含一个隐变量
f
f
f,
f
f
f服从0均值高斯分布,其协方差矩阵
Σ
(
θ
)
\Sigma(\theta)
Σ(θ)是超参数
θ
\theta
θ的确定函数。超参数
θ
\theta
θ概率密度为
q
(
θ
)
。
q(\theta)。
q(θ)。观测数据为
D
D
D,隐变量到数据的似然函数记为
H
H
H。要求的是超参数
θ
\theta
θ。<br>
θ
∼
q
(
θ
)
,
f
∼
N
(
0
,
Σ
(
θ
)
)
,
p
(
D
∣
f
)
=
H
(
f
)
\theta \sim q(\theta), \ \ f \sim N(0, \Sigma(\theta)), \ \ p(D|f) = H(f)
θ∼q(θ), f∼N(0,Σ(θ)), p(D∣f)=H(f)
无法直接写出后验概率
p
(
f
,
θ
∣
D
)
p(f,\theta|D)
p(f,θ∣D),一个直接的方法是用MCMC方法轮流对
f
,
θ
f,\theta
f,θ更新:
已知
D
D
D的条件下,固定
θ
\theta
θ更新
f
f
f:<br>
p
(
f
∣
θ
,
D
)
∝
p
(
f
,
D
∣
θ
)
=
p
(
f
∣
θ
)
⋅
p
(
D
∣
f
,
θ
)
=
p
(
f
∣
θ
)
⋅
p
(
D
∣
f
)
=
N
(
0
,
Σ
(
θ
)
)
⋅
H
(
f
)
p(f|\theta,D) \propto p(f,D|\theta) = p(f|\theta) \cdot p(D|f,\theta) = p(f|\theta)\cdot p(D|f) = N(0,\Sigma(\theta))\cdot H(f)
p(f∣θ,D)∝p(f,D∣θ)=p(f∣θ)⋅p(D∣f,θ)=p(f∣θ)⋅p(D∣f)=N(0,Σ(θ))⋅H(f)</p> </li><li> <p>已知
D
D
D的条件下,固定
f
f
f更新
θ
\theta
θ:<br>
p
(
θ
∣
f
,
D
)
=
p
(
θ
∣
f
)
∝
p
(
θ
)
⋅
p
(
f
∣
θ
)
=
N
(
0
,
Σ
(
θ
)
)
⋅
q
(
θ
)
p(\theta|f,D) =p(\theta|f) \propto p(\theta)\cdot p(f|\theta) = N(0,\Sigma(\theta))\cdot q(\theta)
p(θ∣f,D)=p(θ∣f)∝p(θ)⋅p(f∣θ)=N(0,Σ(θ))⋅q(θ)</p> </li>
两个条件概率都包含一个高斯函数
N
(
0
,
Σ
(
θ
)
)
N(0,\Sigma(\theta))
N(0,Σ(θ)),当
θ
\theta
θ对应的方差较小时,该函数很不均匀(highly peaked)。导致MCMC混合很慢。
解决方法是,另外设定一个超参数
ν
∼
N
(
0
,
I
)
\nu \sim N(0,I)
ν∼N(0,I),是一个各分量独立的标准正态分布,且和
θ
\theta
θ无关。令
L
(
θ
)
L(\theta)
L(θ)为
Σ
(
θ
)
\Sigma(\theta)
Σ(θ)的cholesky分解,则有
L
(
θ
)
T
L
(
θ
)
=
Σ
(
θ
)
L(\theta)^TL(\theta)=\Sigma(\theta)
L(θ)TL(θ)=Σ(θ),
f
=
L
(
θ
)
⋅
ν
f=L(\theta)\cdot \nu
f=L(θ)⋅ν。
使用MCMC方法轮流对
ν
,
θ
\nu, \theta
ν,θ更新:
D
D
D的条件下,固定
θ
\theta
θ更新
ν
\nu
ν:<br>
p
(
ν
∣
θ
,
D
)
∝
p
(
D
∣
ν
,
θ
)
⋅
p
(
ν
,
θ
)
=
H
(
L
(
θ
)
⋅
ν
)
⋅
p
(
ν
)
⋅
p
(
θ
)
∝
H
(
L
(
θ
)
⋅
ν
)
⋅
N
(
ν
;
0
,
I
)
p(\nu|\theta,D) \propto p(D|\nu,\theta)\cdot p(\nu,\theta) = H(L(\theta)\cdot\nu) \cdot p(\nu) \cdot p(\theta) \propto H(L(\theta)\cdot\nu) \cdot N(\nu;0,I)
p(ν∣θ,D)∝p(D∣ν,θ)⋅p(ν,θ)=H(L(θ)⋅ν)⋅p(ν)⋅p(θ)∝H(L(θ)⋅ν)⋅N(ν;0,I)</li><li>已知
D
D
D的条件下,固定
ν
\nu
ν更新
θ
\theta
θ:<br>
p
(
θ
∣
ν
,
D
)
∝
p
(
D
∣
ν
,
θ
)
⋅
p
(
ν
,
θ
)
=
H
(
L
(
θ
)
⋅
ν
)
⋅
p
(
ν
)
⋅
p
(
θ
)
∝
H
(
L
(
θ
)
⋅
ν
)
⋅
q
(
θ
)
p(\theta|\nu,D) \propto p(D|\nu,\theta)\cdot p(\nu,\theta) = H(L(\theta)\cdot\nu) \cdot p(\nu) \cdot p(\theta) \propto H(L(\theta)\cdot\nu) \cdot q(\theta)
p(θ∣ν,D)∝p(D∣ν,θ)⋅p(ν,θ)=H(L(θ)⋅ν)⋅p(ν)⋅p(θ)∝H(L(θ)⋅ν)⋅q(θ)</li>
这种条件概率推导有一定套路:首先利用已知项的概率为常数,获得联合概率:
p
(
A
∣
B
)
∝
p
(
A
,
B
)
p(A|B) \propto p(A,B)
p(A∣B)∝p(A,B)。之后把“原因”挪到“结果”的条件号后面,例如
f
→
D
,
θ
→
f
f\to D, \theta \to f
f→D,θ→f。如果“原因”已经在条件号之后,在变形时略去不看。同时利用独立性进行拆解。</p>
这两个条件概率中虽然也含有高斯分布,但其协方差和待求变量
θ
,
ν
\theta,\nu
θ,ν无关,整个条件概率密度函数较平缓。
由于选择的隐变量
ν
\nu
ν和待求变量
θ
\theta
θ无关,马氏链中后项对前项的决定性小,MCMC算法混合更快。<br> <img src="https://img-blog.csdnimg.cn/img_convert/03175095543f97e9ca2a7da246526371.png" alt="这里写图片描述">
这种拆解隐变量以求解其协方差参数的方法称为reparameterization,在很多论文中都有使用[1](#fn1)。
- Adams, Ryan Prescott, George E. Dahl, and Iain Murray. “Incorporating side information in probabilistic matrix factorization with gaussian processes.” arXiv preprint arXiv:1003.4944 (2010). ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号