【平价数据】GAN用于半监督学习
【平价数据】GAN用于半监督学习
Salimans, Tim, et al. “Improved techniques for training gans.” Advances in Neural Information Processing Systems. 2016.
概述
GAN的发明者Ian Goodfellow2016年在Open AI任职期间发表了这篇论文,其中提到了GAN用于半监督学习(semi supervised)的方法。称为SSGAN。
作者给出了Theano+Lasagne实现。本文结合源码对这种方法的推导和实现进行讲解。[1](#fn1)
半监督学习
考虑一个分类问题。
如果训练集中大部分样本没有标记类别,只有少部分样本有标记。则需要用半监督学习(semi-supervised)方法来训练一个分类器。
wiki上的这张图很好地说明了无标记样本在半监督学习中发挥作用:
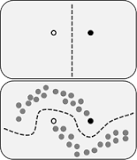
如果只考虑有标记样本(黑白点),纯粹使用监督学习。则得到垂直的分类面。
考虑了无标记样本(灰色点)之后,我们对样本的整体分布有了进一步认识,能够得到新的、更准确的分类面。
核心理念
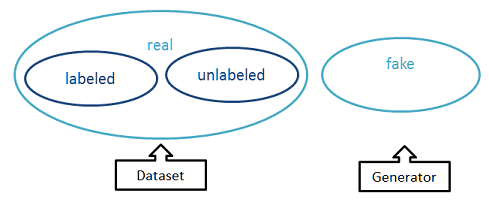
在半监督学习中运用GAN的逻辑如下。
- 无标记样本没有类别信息,无法训练分类器;- 引入GAN后,其中生成器(Generator)可以从随机信号生成伪样本;- 相比之下,原有的无标记样本拥有了人造类别:真。可以和伪样本一起训练分类器。
![这里写图片描述]()
举个通俗的例子:就算没人教认字,多练练分辨“是不是字”也对认字有好处。有粗糙的反馈,也比没有反馈强。
原理
框架
GAN中的两个核心模块是生成器(Generator)和鉴别器(Discriminator)。这里用分类器(Classifier)代替了鉴别器。

训练集中包含有标签样本
x
l
x_l
xl和无标签样本
x
u
x_u
xu。<br> **生成器**从随机噪声生成伪样本
I
f
I_f
If。<br> **分类器**接受样本
I
I
I,对于
K
K
K类分类问题,输出
K
+
1
K+1
K+1维估计
l
l
l,再经过softmax函数得到概率
p
p
p:其前
K
K
K维对应原有
K
K
K个类,最后一维对应“伪样本”类。<br>
p
p
p的最大值位置对应为估计标签
y
y
y。
s
o
f
t
m
a
x
(
x
i
)
=
exp
(
x
i
)
∑
j
exp
(
x
j
)
{\rm softmax}(x_i)=\frac{\exp (x_i)}{\sum_j \exp(x_j)}
softmax(xi)=∑jexp(xj)exp(xi)</p>
三种误差
整个系统涉及三种误差。
对于训练集中的有标签样本,考察估计的标签是否正确。即,计算分类为相应的概率:
L
l
a
b
e
l
=
−
E
[
ln
p
(
y
∣
x
)
]
L_{label}=-E\left[ \ln p(y|x)\right]
Llabel=−E[lnp(y∣x)]
对于训练集中的无标签样本,考察是否估计为“真”。即,计算不估计为
K
+
1
K+1
K+1类的概率:<br>
L
u
n
l
a
b
e
l
=
−
E
[
ln
(
1
−
p
(
K
+
1
∣
x
)
)
]
L_{unlabel} = -E\left[ \ln \left( 1 - p(K+1|x)\right) \right]
Lunlabel=−E[ln(1−p(K+1∣x))]
对于生成器产生的伪样本,考察是否估计为“伪”。即,计算估计为
K
+
1
K+1
K+1类的概率:<br>
L
f
a
k
e
=
−
E
[
ln
p
(
K
+
1
∣
x
)
]
L_{fake} = -E\left[ \ln p(K+1|x) \right]
Lfake=−E[lnp(K+1∣x)]
推导
考虑softmax函数的一个特性:
s
o
f
t
m
a
x
(
x
i
−
c
)
=
exp
(
x
i
−
c
)
∑
j
exp
(
x
j
−
c
)
=
exp
(
x
i
)
/
e
x
p
(
c
)
∑
j
exp
(
x
j
)
/
exp
(
c
)
=
s
o
f
t
m
a
x
(
x
i
)
{\rm softmax}(x_i-c)=\frac{\exp (x_i-c)}{\sum_j \exp(x_j-c)}=\frac{\exp (x_i)/exp(c)}{\sum_j \exp(x_j) /\exp(c)}={\rm softmax}(x_i)
softmax(xi−c)=∑jexp(xj−c)exp(xi−c)=∑jexp(xj)/exp(c)exp(xi)/exp(c)=softmax(xi) 于是,可以令
l
→
l
−
l
K
+
1
l\to l-l_{K+1}
l→l−lK+1,有
l
K
+
1
=
0
l_{K+1}=0
lK+1=0,
p
=
s
o
f
t
m
a
x
(
l
)
p={\rm softmax}(l)
p=softmax(l)保持不变。
期望号略去不写,利用
exp
l
K
+
1
=
1
,
\exp l_{K+1}=1,
explK+1=1,后两种代价变为:<br>
L
u
n
l
a
b
e
l
=
−
ln
[
1
−
p
(
K
+
1
∣
x
)
]
=
−
ln
[
∑
j
=
1
K
exp
l
j
∑
j
=
1
K
exp
l
j
+
exp
l
K
+
1
]
=
−
ln
[
∑
j
=
1
K
exp
l
j
]
+
ln
[
1
+
∑
j
=
1
K
exp
l
j
]
L_{unlabel}=-\ln \left[1 - p(K+1|x)\right]=-\ln \left[\frac{\sum_{j=1}^K \exp l_j}{\sum_{j=1}^K \exp l_j +\exp l_{K+1}}\right]= -\ln\left[ \sum_{j=1}^K \exp l_j\right] + \ln \left[ 1+\sum_{j=1}^K \exp l_j\right]
Lunlabel=−ln[1−p(K+1∣x)]=−ln[∑j=1Kexplj+explK+1∑j=1Kexplj]=−ln[j=1∑Kexplj]+ln[1+j=1∑Kexplj]
L
f
a
k
e
=
−
ln
[
p
(
K
+
1
∣
x
)
]
=
ln
[
1
+
∑
j
=
1
K
exp
l
j
]
L_{fake}=-\ln \left[p(K+1|x)\right]=\ln \left[ 1+\sum_{j=1}^K \exp l_j\right]
Lfake=−ln[p(K+1∣x)]=ln[1+j=1∑Kexplj]
上述推导可以让我们省去
l
K
+
1
l_{K+1}
lK+1,<strong>让分类器仍然输出K维的估计
l
l
l</strong>。
对于第一个代价,由于分类器输入必定来自前K类,所以可以直接使用
l
l
l的前K维:<br>
L
l
a
b
e
l
=
−
ln
[
p
(
y
∣
x
,
y
<
K
+
1
)
]
=
−
ln
[
exp
l
y
∑
j
=
1
K
exp
l
j
]
=
−
l
y
+
ln
[
∑
j
=
1
K
exp
l
j
]
L_{label}=-\ln\left[ p(y|x,y<K+1)\right]=-\ln \left[\frac{\exp l_y}{\sum_{j=1}^K \exp l_j}\right]=-l_y + \ln\left[ \sum_{j=1}^K \exp l_j\right]
Llabel=−ln[p(y∣x,y<K+1)]=−ln[∑j=1Kexpljexply]=−ly+ln[j=1∑Kexplj]
引入两个函数,使得书写更为简洁:
L
S
E
(
x
)
=
ln
[
∑
j
=
1
exp
x
j
]
{\rm LSE}(x)=\ln\left[ \sum_{j=1} \exp x_j\right]
LSE(x)=ln[j=1∑expxj]</p>
s o f t p l u s ( x ) = ln ( 1 + exp x ) {\rm softplus}(x)=\ln(1+\exp x) softplus(x)=ln(1+expx)
三个误差:
L
l
a
b
e
l
=
−
l
y
+
L
S
E
(
l
)
L_{label}=-l_y +{\rm LSE}(l)
Llabel=−ly+LSE(l)
L
u
n
l
a
b
e
l
=
−
L
S
E
(
l
)
+
s
o
f
t
p
l
u
s
(
L
S
E
(
l
)
)
L_{unlabel}=-{\rm LSE}(l)+{\rm softplus}({\rm LSE}(l))
Lunlabel=−LSE(l)+softplus(LSE(l))
L
f
a
k
e
=
s
o
f
t
p
l
u
s
(
L
S
E
(
l
)
)
L_{fake}={\rm softplus}({\rm LSE}(l))
Lfake=softplus(LSE(l))
优化目标
对于分类器来说,希望上述误差尽量小。引入权重
w
w
w,得到**分类器优化目标**:<br>
L
D
=
L
l
a
b
e
l
+
w
2
(
L
u
n
l
a
b
e
l
+
L
f
a
k
e
)
L_D = L_{label}+\frac{w}{2}(L_{unlabel}+L_{fake})
LD=Llabel+2w(Lunlabel+Lfake)
对于生成器来说,希望其输出的伪样本能够骗过分类器。生成器优化目标与分类器的第三项相反:
L
G
=
−
L
f
a
k
e
L_G = -L_{fake}
LG=−Lfake
实验
本文的实验包含三个图像分类问题。分类器接受图像
x
x
x,输出
K
K
K类分类结果
l
l
l。生成器从均匀分布的噪声
z
z
z生成一张图像
x
x
x。
MNIST
10分类问题,图像为28*28灰度。
生成器是一个3层线性网络:
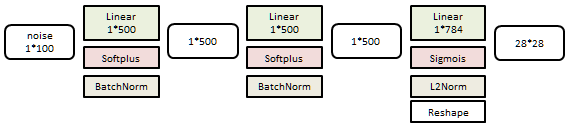
分类器是一个6层线性网络:
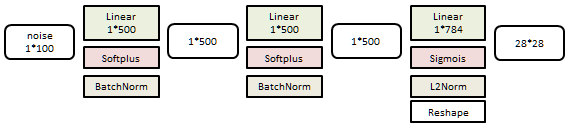
训练样本60K个,测试样本10K个。
选择不同数量的训练样本给予标记,考察测试样本中错误个数。使用不同随机数种子重复10次:
| 有标记样本 | 20 | 50 | 100 | 200 |
|---|---|---|---|---|
| 占比 | 0.033% | 0.083% | 0.17% | 0.33% |
| 错误个数 | 1677±452 | 221±136 | 93±6.5 | 90±4.2 |
Cifar10
10分类问题,图像为32*32彩色。
生成器是一个4层反卷积网络:

分类器是一个9层卷积网络:
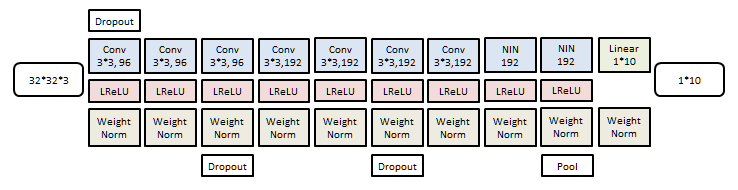
训练样本50K个,测试样本10K个。
选择不同数量的训练样本给予标记,考察测试样本中错误个数。使用不同的测试/训练分割重复10次:
| 有标记样本 | 1000 | 2000 | 4000 | 8000 |
|---|---|---|---|---|
| 占比 | 2% | 4% | 8% | 16% |
| 错误个数 | 21.83±2.01 | 19.61±2.09 | 18.63±2.32 | 17.72±1.82 |
SVHN
10分类问题,图像为32*32彩色。
生成器(上)以及分类器(下)和CIFAR10的结构非常类似。
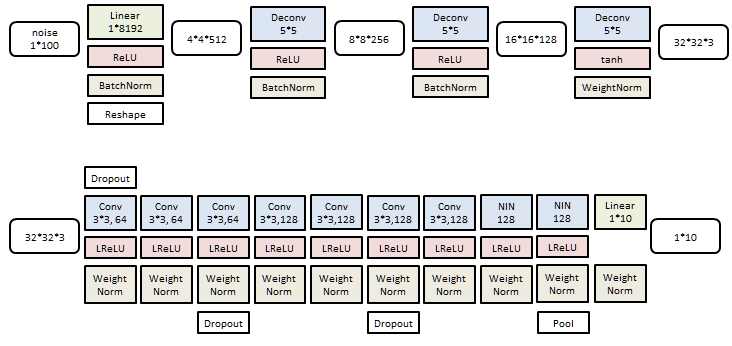
训练样本73K,测试样本26K。
选择不同数量的训练样本给予标记,考察测试样本中错误个数。使用不同的测试/训练分割重复10次:
| 有标记样本 | 500 | 1000 | 2000 |
|---|---|---|---|
| 占比 | 0.68% | 1.4% | 2.7% |
| 错误个数 | 18.84±4.8 | 8.11±1.3 | 6.16±0.58 |
- USC的Shao-Hua Sun也给出了一个Tensorflow实现。但没有处理训练集中的无标签样本,个人认为对原文理解有偏差。 ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号