【时间序列】时间序列分割聚类算法TICC
【时间序列】时间序列分割聚类算法TICC
Hallac, David, et al. “Toeplitz Inverse Covariance-Based Clustering of Multivariate Time Series Data.” KDD. (2017).
本文是2017年KDD最佳论文,解决了高维时间信号的自动分割聚类问题,并给出了基于python的源码(戳这里下载)。
核心思想
在实际问题中有大量随时间变化的高维信号。
- 驾驶汽车:油门,刹车,地理位置,空调,门窗…- 支付软件:用户的登陆,转入,提现,消费… 在没有标定的情况下,想发掘这些数据中隐藏的信息,即将信号划分为若干可能的状态,并标记每条信号的各段。
- 驾驶汽车:起步,上坡,超车,拥堵…- 支付软件:用户发薪,过节,打新股… 这就需要同时对数据进行两种操作:
- 将各条数据进行分割- 将分割结果各个聚类
传统聚类方法考察信号各维度的绝对值,以确定信号间的相似度;
本文算法考察信号各维度之间的相关性,以确定信号间的相似度。
建模
信号段
设有时间长度为
T
T
T的原始信号<br>
x
=
[
x
1
,
x
2
.
.
.
x
T
]
\textbf {x}=\left[ x_1, x_2...x_T\right]
x=[x1,x2...xT]
实际应用中,会有来自多个用户的多段原始信号。这里可以直接将它们连缀成一个向量。如果需要考虑绝对时刻,则可以将时间戳也作为一维信号增补上去。
其中每一时刻的信号
x
i
x_i
xi为
n
n
n维向量。
为了便于考察信号相关性,以每一时刻为基准,向前截取宽度为
w
w
w的一段:<br>
X
i
=
[
x
i
−
w
+
1
,
.
.
.
x
i
−
1
,
x
i
]
X_i=\left[ x_{i-w+1},...x_{i-1}, x_i\right]
Xi=[xi−w+1,...xi−1,xi]
i
=
1
,
2...
T
i=1,2...T
i=1,2...T<br> 信号段
X
i
X_i
Xi为
n
w
nw
nw维向量。
类别信息
预期将所有信号段划分为
K
K
K类,属于第
j
j
j类的信号段序号集合记为
P
j
,
j
=
1
,
2...
K
P_j, j=1,2...K
Pj,j=1,2...K。
举例:有信号段ABAAC,
n
=
5
n=5
n=5,
K
=
3
K=3
K=3。
P
1
=
[
0
,
2
,
3
]
,
P
2
=
[
1
]
,
P
3
=
[
4
]
P_1=[0, 2, 3], P_2=[1], P_3=[4]
P1=[0,2,3],P2=[1],P3=[4]</p>
认为每一类信号段服从0均值高斯分布,其协方差逆矩阵为
Θ
j
,
j
=
1
,
2...
K
\Theta_j, j=1,2...K
Θj,j=1,2...K。这是一个
n
w
×
n
w
nw \times nw
nw×nw的矩阵。
Θ
i
\Theta_i
Θi由
w
×
w
w\times w
w×w个子矩阵组成,每个子矩阵的尺寸为
n
×
n
n\times n
n×n。位置
p
q
pq
pq的子矩阵描述时刻
p
p
p和时刻
q
q
q之间,
n
n
n个维度之间的协方差逆矩阵。<br>
[
0
−
w
+
1
,
.
.
.
p
,
.
.
.
q
,
.
.
.
0
]
[0-w+1, ... p, ...q, ...0]
[0−w+1,...p,...q,...0]<br> 这里假设信号是非时变的,不同时刻信号之间的关系**只和相对时间差有关**;交换pq,其**协方差逆阵互为转置**。
换句话说,
Θ
j
\Theta_j
Θj是个分块Toeplitz矩阵: 每条斜线上的子矩阵相同;对角对称斜线的子矩阵互为转置。
求解
我们需要轮流求解两个问题
Θ
j
\Theta_j
Θj,求解信号段分类方法
P
j
P_j
Pj</li><li>给定
P
j
P_j
Pj,求解各类逆协方差阵
Θ
j
\Theta_j
Θj</li>
信号段分类
P
j
P_j
Pj
给定
Θ
j
\Theta_j
Θj,把信号段
X
i
X_i
Xi归入
j
j
j类的代价可以负对数似然表示:<br>
E
(
i
∈
P
j
)
=
−
l
l
(
i
,
j
)
=
−
log
[
N
(
X
i
;
0
,
Θ
j
−
1
)
]
E(i\in P_j)=-ll(i,j)=-\log \left[ N(X_i;0,\Theta_j^{-1})\right]
E(i∈Pj)=−ll(i,j)=−log[N(Xi;0,Θj−1)]
=
−
log
[
det
(
Θ
j
)
1
/
2
⋅
exp
[
−
1
2
X
i
T
Θ
j
X
i
]
]
=
−
log
det
(
Θ
j
)
+
X
i
T
Θ
j
X
i
=-\log \left[ \det(\Theta_j)^{1/2} \cdot \exp \left[ -\frac{1}{2}X_i^T\Theta_jX_i\right] \right]=-\log \det(\Theta_j) + X_i^T\Theta_jX_i
=−log[det(Θj)1/2⋅exp[−21XiTΘjXi]]=−logdet(Θj)+XiTΘjXi
另外考虑信号的连续性:相连信号段不同类时施加惩罚
β
\beta
β。<br>
E
(
i
,
i
+
1
)
=
{
0
i
,
i
+
1
同
类
β
i
,
i
+
1
不
同
类
E(i,i+1)=\begin{cases}0 & i,i+1同类\\ \beta & i,i+1不同类\end{cases}
E(i,i+1)={<!-- -->0βi,i+1同类i,i+1不同类
两个代价构成经典的流水线调度问题,可以使用BP算法求解。 其核心思路是:在给第i个信号段分类时,只需考虑第i-1信号段分为各类时的代价即可。
逆协方差阵
Θ
j
\Theta_j
Θj
给定一类中所有信号段集合
P
j
P_j
Pj,通过最小化其负对数似然总和,可以求解
Θ
j
\Theta_j
Θj。<br> 各类可以并行计算,故书写时省去下标j。
E
(
Θ
)
=
∑
i
∈
P
−
l
l
(
X
i
,
Θ
)
=
∑
i
∈
P
−
log
det
(
Θ
)
+
X
i
T
Θ
X
i
=
E
1
+
E
2
E(\Theta)=\sum_{i \in P} -ll(X_i, \Theta)=\sum_{i \in P} -\log \det(\Theta) + X_i^T\Theta X_i=E_1 + E_2
E(Θ)=i∈P∑−ll(Xi,Θ)=i∈P∑−logdet(Θ)+XiTΘXi=E1+E2
求和号内第一项和
j
j
j无关,
∣
∣
||
∣∣表示集合内元素计数:<br>
E
1
=
−
∣
P
i
∣
⋅
log
det
(
Θ
)
E_1=-|P_i|\cdot \log \det (\Theta)
E1=−∣Pi∣⋅logdet(Θ)
求和号内第二项可以写成迹的形式:
E
2
=
−
t
r
(
∑
i
∈
P
X
i
T
X
i
)
=
−
∣
P
i
∣
⋅
t
r
(
S
⋅
Θ
)
E_2=-tr(\sum_{i\in P}X_i^TX_i)=-|P_i|\cdot tr(S\cdot \Theta)
E2=−tr(i∈P∑XiTXi)=−∣Pi∣⋅tr(S⋅Θ)
其中
S
S
S是由
P
j
P_j
Pj中所有信号段计算得到的当前协方差阵。<sup class="footnote-ref">[1](#fn1)</sup>
另外添加一个正则项:
E
3
=
∣
∣
λ
⊙
Θ
∣
∣
1
E_3=||\lambda \odot \Theta||_1
E3=∣∣λ⊙Θ∣∣1<br> 其中
λ
\lambda
λ为权重矩阵,
⊙
\odot
⊙表示矩阵对位相乘。
根据前述,要求
Θ
\Theta
Θ是分块Toeplitz矩阵。
把问题稍作变换为如下形式,可以用ADMM[2](#fn2)算法快速求解:
m
i
n
i
m
i
z
e
−
log
det
Θ
+
t
r
(
S
⋅
Θ
)
+
∥
∣
λ
⊙
Z
∣
∣
1
minimize\ -\log \det \Theta+tr(S\cdot \Theta) + \||\lambda\odot Z||_1
minimize −logdetΘ+tr(S⋅Θ)+∥∣λ⊙Z∣∣1
s
u
b
j
e
c
t
t
o
Θ
=
Z
,
Z
为
分
块
T
o
e
p
l
i
t
z
矩
阵
subject\ to\ \Theta=Z, Z为分块Toeplitz矩阵
subject to Θ=Z,Z为分块Toeplitz矩阵
实验
正确率
使用模拟数据:信号维度
n
=
5
n=5
n=5,窗口宽度
w
=
5
w=5
w=5。聚类数量
K
K
K从2到4不等。每个实验包含
100
K
100K
100K个样本。<br> 试验中直接固定
K
K
K为真值。使用所有聚类的[F1 score](https://en.wikipedia.org/wiki/F1_score)均值作为聚类质量评估。
可以看到,本文的TICC算法(第一行)有十分明显的优势。
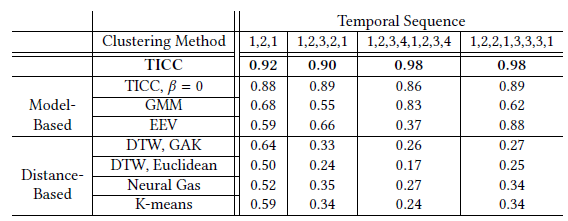
TICC算法(蓝方块)聚类所需的样本数也较少。
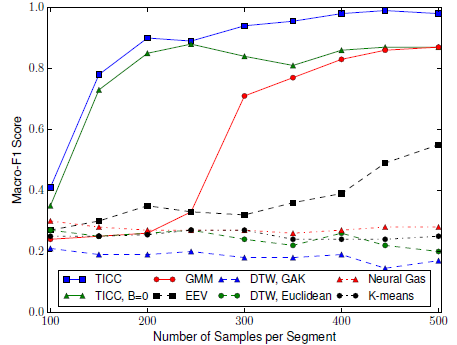
可扩展性
使用
n
=
50
n=50
n=50的高维样本,聚类数量
K
=
5
K=5
K=5,窗口宽度
w
=
3
w=3
w=3。下图示出,当信号长度增加时,聚类时间的增长基本为线性。<br> <img src="https://img-blog.csdnimg.cn/img_convert/36d890916cf33d9c1e2c9c29281e5e19.png" alt="这里写图片描述">
真实案例
给出了汽车行驶案例,大家体会一下。
传感器
n
=
7
n=7
n=7
- 刹车状态- 前向加速度- 侧向加速度- 方向盘角度- 速度- 发动机转速- 油门状态 每一组观测时长1小时,每隔0.1秒采样一次。共有36000组观测。
使用的窗口
w
=
10
w=10
w=10时长1秒。
使用BIC方法[3](#fn3)发现的最佳聚类数量为
K
=
5
K=5
K=5。人工观察,它们对应于如下状态:<br> <img src="https://img-blog.csdnimg.cn/img_convert/f1001500d518c4e4582bf7670c96072b.png" alt="这里写图片描述">
此处待推导。思路:证明
X
i
T
Θ
X
i
X_i^T\Theta X_i
XiTΘXi是
S
⋅
Θ
S\cdot \Theta
S⋅Θ的特征值。其总和为该矩阵的迹。 [↩︎](#fnref1)</p> </li>1. S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011. [↩︎](#fnref2) 1. T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning. Springer, 2009. [↩︎](#fnref3)
转载于网络 侵权联系作者立即删除QAQ


 浙公网安备 33010602011771号
浙公网安备 33010602011771号