BUAA_OO_第三单元总结
本单元要求动态维护一个社交网络,涉及了社交网络中人员、讨论组以及消息的交流和分发。在维护社交网络数据的基础上,也必须维护社交网络的结构信息(当然本质上也是数据)。总体而言,本单元任务架构分层相对比较清晰,由于JML语言的存在,理解相对而言也不容易出现偏差,虽然对于图论算法有了一定要求,但实际涉及的算法和数据结构都属于比较简单的一类,同时又有Java内置的各种常用数据结构的支持,难度相对于前几单元还是有所下降的。
第一次作业
首次作业仅仅提供了一个社交网络的雏形,仅需简单实现person、group、network以及相应的异常类即可。同时,类之间的数据交换较少且比较直接,定义的方法也较为简单。唯一难度较高的可能是查询连通性的操作,但即使选择使用BFS或者DFS也不会产生任何问题。
第二次作业
本次作业对首次作业进行了一定扩展,主要是增添了社交网络中信息交流的功能,具体而言,增设了Message类并定义了相关操作,如注册信息、发送信息和查询信息等。同时,启用了首次作业中实际并未使用的部分方法(如queryAgeVar等)。此外,新增了一个明显的图论算法需求——最小生成树。
第三次作业
本次作业主要集中在对社交网络中信息交流的进一步细化,具体而言,对message进行了扩展,出现了红包(RedEnvelope)、表情消息(EmojiMessage)和通知消息(NoticeMessage)等,同时增设了各自独有以及配套的操作,红包涉及Person属性Money的更改,表情消息设计NetWork中表情热度的修改,通知消息则涉及通知清空的操作。同时,也增加了对最短路径算法的需求。
架构设计功能分析
本部分将简要列举第一次作业和第二次作业,以第三次作业为基础进行具体分析
第一次作业
counter软件包
本软件包保存计数器工具类

graph软件包
本软件包下辖三个软件包,通过图的方式存储NetWork中的关系
adjacencytable软件包
本软件包实现了邻接表的保存,存储点与点之间的相对关系

AdjacencyTable类
本类为邻接表的主结构,保存了表中的所有点
Edge类
本类为邻接表中边的记录
Vertex类
本类为邻接表中点的记录,保存了以此点为起始的所有边
subgraph软件包
本软件包保存了指定子图的关系,实际对应了Group中的关系

SubGraph类
本类即保存了子图的相关信息
unionfind软件包
本软件包实现了并查集结构

UnionFind类
本类为并查集的主结构
Point类
本类为并查集中的点
Graph类
本类通过将AdjacencyTable、SubGraph、UnionFind类作为属性,统一维护全图的所有信息
myexception软件包
即包含了所有继承的异常类,分别利用Counter类实现了基本功能

mygroup软件包
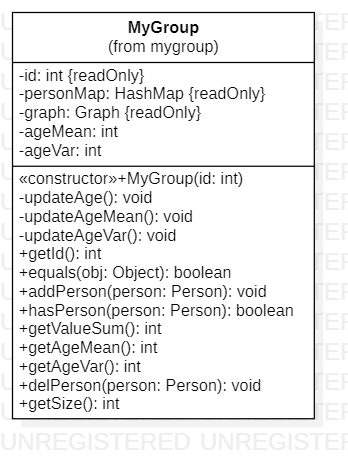
mynetwork软件包

myPerson软件包

第二次作业
algorithm软件包
保存本次作业中需要用到的算法类

counter软件包
同第一次作业

myexception软件包

mymessage软件包

mynetwork软件包

mygroup软件包

myperson软件包

structure软件包
实际为第一次作业的graph软件包,略微调整了层次架构
adjacencytable软件包
同第一次作业
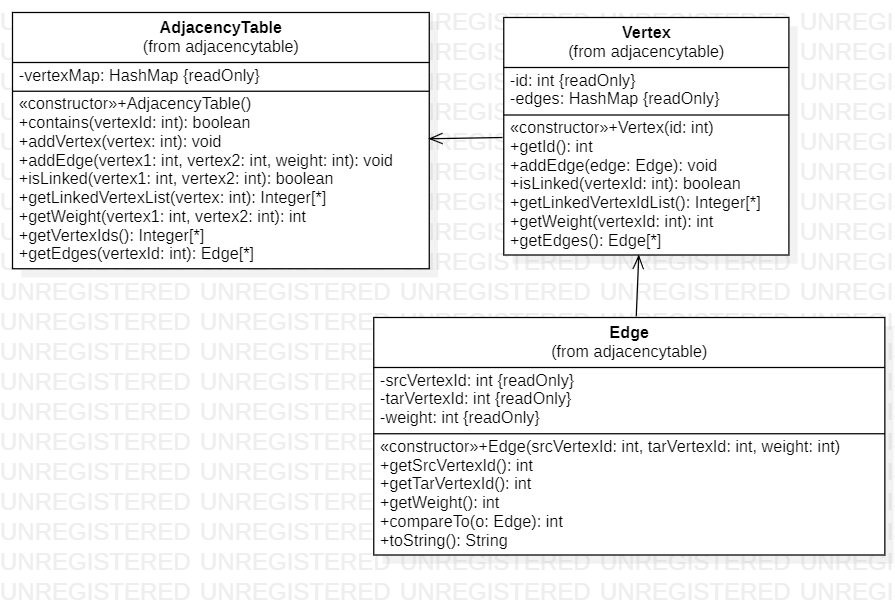
graph软件包
将子图和全图均放置在本软件包

unionfind软件包
同第一次作业

第三次作业
本次作业实现了完整的架构,现从各软件包、各类以及关键方法的功能进行分析
algorithm 软件包
顾名思义,本软件包保存了作业中需要使用的两个算法类,即克鲁斯卡尔和迪杰斯特拉。

Dijkstra 类
迪杰斯特拉算法的工具类,内置唯一一个静态方法 getShortestPath() 以获得最短路径
// 获取最短路径
// 使用堆优化
// 一旦更新到目标点则立即返回值
public static int getShortestPath(
int srcVertexId, int tarVertexId, AdjacencyTable adjacencyTable);
Kruskal 类
克鲁斯卡尔算法的工具类,同样内置唯一一个静态方法 getMinimumSpanningTreeWeightSum() 获取最小生成树的权值和
// 邻接表+并查集
public static int getMinimumSpanningTreeWeightSum(UnionFind unionFind, ArrayList<Edge> edges)
counter 软件包

Counter 类
异常类中的计数工具类,提供方法更新和获取次数
structure 软件包
本软件包保存了本次作业中需要使用的关键数据结构,包括图、邻接表、并查集
adjacencytable 软件包
本软件包实现了邻接表的数据结构

Edge 类
邻接表中的边结构,单向边,记录了起始点和终点
Vertex 类
邻接表中的点结构,保存了以此点为起始点的所有边数据
AdjacencyTable 类
邻接表的主结构,提供边查询等功能
graph 软件包

本软件包实现了图结构,包括全图和子图
SubGraph 类
本类实现了子图,子图将维护子图中的边权和等信息
Graph 类
本类实现了全图,维护了子图,连通性等信息,同时实现了单例模式
unionFind 软件包
本软件包实现了并查集

Vertex 类
本类保存了并查集中一个点的信息,即其父亲、秩
UnionFind 类
本类为并查集的工具类,实现了合并、查询等操作,并且实现了路径压缩和按秩合并
myexception 软件包
本软件包中保存了所有继承的异常类
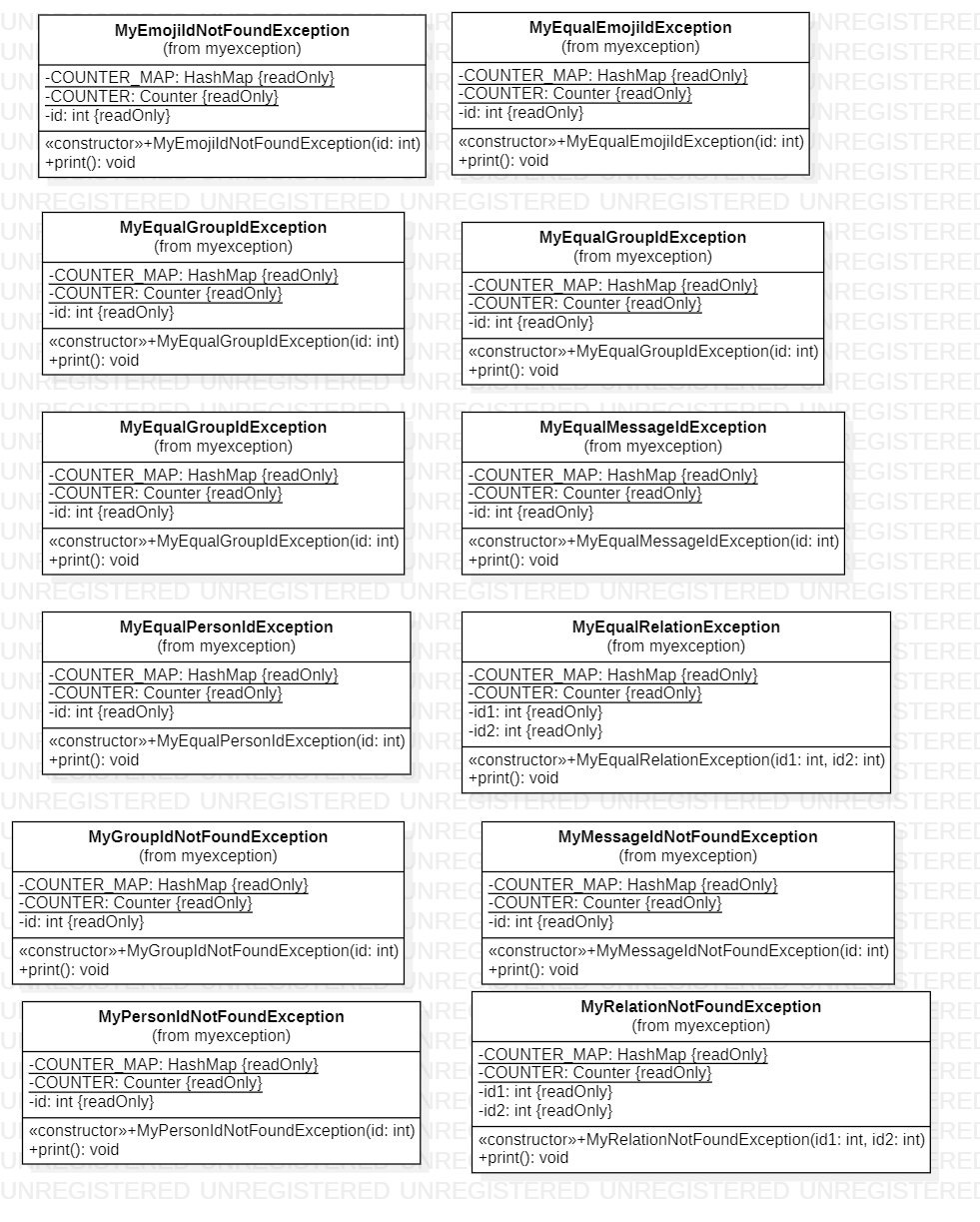
mynetwork 软件包
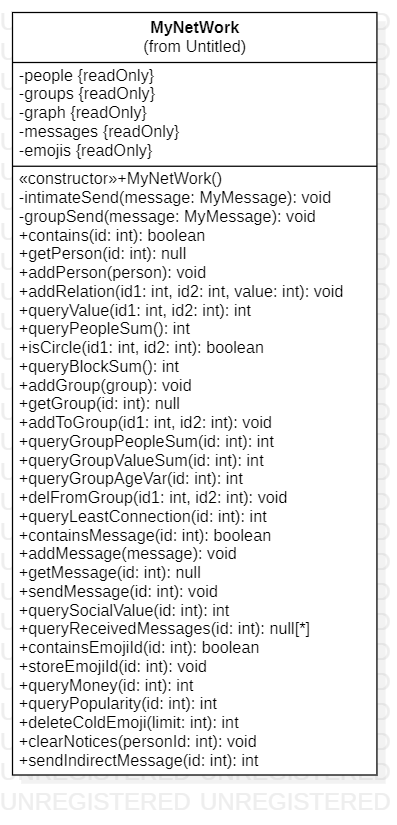
MyNetWork 类
继承了官方接口
mygroup 软件包

MyGroup 类
继承了官方接口,同时提供了部分自定义函数便于处理,
// 为组中所有person增加指定的社交值
public void addSocialValue(int num);
// 为组中所有person增加指定数量的金钱
public void addMoney(int num);
myperson 软件包

MyPerson 类
继承了官方接口,同时提供了部分自定义函数便于处理
// 添加消息进入消息列表
public void addMessage(Message message);
// 清空notice
public void clearNoticeMessages();
mymessage 软件包
实现了官方的各种Message接口

模型构建及维护策略
本单元模型构建较为简单,本质上NetWork作为顶层结构,而Group、Person、Message均作为其子结构,其中Group可对Person进行一定的管理,同时,Group、Person均可对Message进行管理
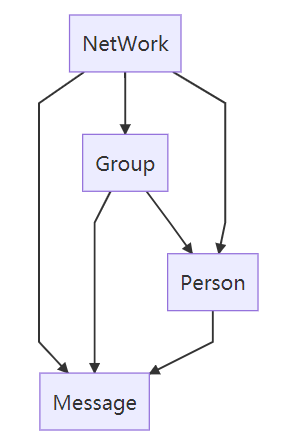
信息存储
图关系存储
本处对应的图关系,包括图中的所有节点、边以及子图等关系,对应于作业而言,即NetWork作为全图,Group作为子图,Person作为顶点,link作为边
图关系存储采用了独立的结构 structure-->graph-->Graph进行存储,在前面的叙述中已经提到,Graph对外提供了一个唯一的静态实例,该实例对所有其他类公开,其唯一性自然也保证互相共享
而如此做的原因出于如下几点:
-
NetWork的唯一性
NetWork的唯一性是可行的基础,既然NetWork唯一,那么对应的图也就唯一,静态单例自然也就可行
-
各级查询依赖
很明显,对于NetWork、Group、Person均对图关系的查询有一定需求,如果采取直接在NetWork中保存,或非静态实例作为NetWork的一个属性,则必须在NetWork中配置相应的访问方法,并需要将自身作为Group、Person的一个属性,非但提高了代码量,也破坏了自顶向上的层次结构,出现了循环关系
-
操作易维护
图关系包含了众多相关关系的存储,如果放在NetWork中,将导致NetWork过于复杂,通过由Graph维护,对外提供有限的方法进行修改和查询,在修改时内部自动实现信息的更新,极大的提高了安全性
其余信息存储
我曾考虑过将NetWork等完全作为一个查询接口,信息完全由其他类维护,但是此法将需要至少3个类,同时,配置了大量方法,反倒降低了安全性,因此,便由其自身存储
信息维护
信息维护对应的便是信息查询,此处便结合关键操作进行维护说明
queryValue
本质上即为询问边权,由Graph在添加关系时,记录边权至邻接表即可
isCircle
本质上即为询问连通性,Graph在添加关系时,也会在并查集中进行合并操作,由并查集的维护连通性
queryBlockSum
本质上即为询问连通块数目,此处也由并查集进行维护,显然并查集中每加入一个点,连通块数目便+1,每次添加关系时,若成功合并,则连通块数目-1
queryLeastConnection
询问最小生成树,对于最小生成树,其实是有办法以较小的代价进行动态维护的(如破圈算法甚至更高级的lct等),但是,指令数目本身存在限制,额外添加维护反倒降低了安全性,不如直接仅维护基本的点边关系
queryGroupValueSum
询问边权和,由Graph中的SubGraph进行维护,本信息将在如下情况下更新
-
group中Person的增减
-
relation的增加
queryGroupAgeVar
询问年龄方差,本信息是可以做到动态维护,O(1)查询的,显然首先维护一个年龄总和和一个年龄方差总和,由如下公式可得
(ageQuadraticSum - 2 * ageSum * ageMean + ageMean * ageMean * people.size()) / people.size()
sendIndirectMessage
本质上即为寻找最短路径,动态维护最短路径几乎是很难做到的(考虑时间复杂度不能达到O(n^2)),同时指令条数也存在限制,那么临时计算即可
架构心得
与历次作业相似,本次作业架构的构建实际并不轻松,尤其是在第一次和第二次作业上对架构的实现非常纠结。
在第一次作业时,我主要在思考如何储存Person的acquaintance以及如何计算GroupValueSum等,最终选择了一个更加抽象和独立的图结构进行储存,这也让我试图将NetWork、Group、Person的信息完全剥离出来。
在第二次作业时,更是纠结的高峰,我始终想要将NetWork、Group、Person完全的工具化,同时,并不想为Group、Person增加接口定义之外的public方法,但是信息完全剥离,在效率上又有点不如人意。
更令我纠结的是,什么样的信息该独立储存,什么样的信息该自己保存呢,这个涉及到了作业的整体思路和分工,如果分工不够统一本身便很容易造成错误。
最终,形成了如上的架构。整体而言,架构逻辑上分为两大层次,抽象层次和具体层次。抽象层次对应的便是algorithm和structur两个软件包,其实现了一定的算法和数据结构,本身并无特定意义,而NetWork等具体层次借助抽象层次的方法对信息进行维护和查询,这点在类中方法的命名便可体现出来,前者都是诸如AddVertex、AddEdge之类,后者则是AddPerson、addRelation等。抽象与具体分开,并一一对应,避免了业务类中涉及过多的逻辑操作导致臃肿,同时也变相实现了功能的模块化,提高了可扩展性。
性能要求的满足
本单元对性能提出了一定的要求,对于不限定指令数上限的指令,其复杂度必须保证在O(n)以下,基本而言,有如下几方面的要求
更新后及时处理和保存
在每次更新类指令执行时,提前做好一定的预处理工作。基本的例如对于Group中人年龄、权值和等完全可以在更新时进行计算。同时,
同数据的不同容器保存
对于同样的数据,不同容器进行存储也是有一定必要的,如HashMap和ArrayList的结合使用等。
容器的选择
此外,对于容器的选择也是应该注意的,HashMap和ArrayList的差异较为明显,很容易选择,但是,例如对于Person内部消息的存储,LinkedMessage显然是比ArrayList更优的选择,对于queryRecievedMessage而言两者基本没有区别,甚至ArrayList更快,但是对于clearNotice方法,LinkedMessage使用removeIf进行遍历删除时,仅仅是O(n)的复杂度,对于ArrayList遍历删除,就是O(n^2)了,当前,你也可以选择新建一个ArrayList,将原有ArrayList的内容选择性进行复制,但是,此时又涉及了空间的重新申请,尤其是ArrayList的动态扩容是个时间开销大户。(当然,这个互测数据量限制用ArrayList也基本没啥大问题)
错误修复
本单元的错误其实仍然主要分为实现时典型的考虑不够完整和对题意理解不足等。由于单纯的比如变量名使用错误等并无参考意义,这里仅仅简单列举一下我遇到的一些题意理解问题。
QueryValueSum
本方法极其容易仅仅计算一半的权值,然而实际上仔细阅读Jml可知,此处的内外两层for循环均是遍历了所有了Group中的所有Person。如果以边权和来理解,那么此处的图必须理解为有向图,addRealtion会同时在两个顶点间建立两条权值相同、方向相反的单向边,统计Group所在子图中边的权值和时,显然每条单向边的权值均会被记入。
QueryRecievedMessage
本方法很容易理解为最多返回三条,尤其注意以0开始时,<=3实际上等于于我们理解的<4
AddGroup
注意,在Group人数达到1111时,不应该再加入人进入Group。由于在首次作业中指令条数保证了不可能导致Group中出现超过1000人,导致此处Bug在首次作业的强测和互测中均不会被发现,极有可能将此处Bug延续到第二次作业。
QueryAgeVar
注意,不能直接使用年龄和的平方和年龄的平方和进行计算,在计算平均值时使用了向下取整,此时是会造成精度损失的。
数据构造
本单元仍然主要采用自动评测的方法,搭建评测机,通过与一组人进行互拍以寻找错误。
那么本单元的关键就在于评测机对于指令的覆盖性和针对。
在第一次作业中,指令条数较少,仅仅通过在类中设定相应的静态常量作为调整即可。
自第二次作业开始,方法数目增多,仅仅通过一味的堆砌数据量并不现实,同时,考虑到评测机运行不可能仅在我自己的电脑上运行,提供给其他成员一定的修改方法显然是必要的。因此,在第二单元通过提供一个固定的txt文档,并在评测前进行读取,以实现可控性。
第三次作业,考虑到指令数进一步增多,参数文档采用了更加直观的xml格式。
下一步便是如何选定参数。
在参数设计中,主要涉及了各指令出现的频率以及指令中指定id复用的概率等等。首先,指令整体而言可以分为两种——更新类和查询类,对于限定的指令数,更新类指令显然应该占据最大的份额,查询类指令更多是作为验证。其次,指令整体可分为消息收发测试、最小生成树构建等等,可以通过关闭其他指令做到类似于单元测试的效果。
扩展
// 为指定产品生产商选择广告商
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].euqals(getPerson(procuderId)) && people[i] instanceof Producer);
@ requires (\exists int i; 0 <= i && i < people.length; people[i].equals(getPerson(procuderId)) && people[i] instanceof Advertiser);
@ assignable getPerson(producerId).advertisers;
@ assignable getPerson(AdvertiserId).producers;
@ ensures getPerson(producerId).advertisers.length == \old(getPerson(producerId).advertisers.length) + 1;
@ ensures (\exists int i;0 <= i < getPerson(producerId).advertisers.length;getPerson(producerId).advertisers[i].equals(getPerson(AddVertiserId)));
@ ensures (\forall int i; 0 <= i && i < \old(getPerson(producerId).advertisers.length;
@ \exists int j;0 <= j < getPerson(producerId).advertisers.length;
@ \old(getPerson(producerId).advertisers[i]).euqals(getPerson(producerId).advertisers[j]));
@ ensures (\exists int i;0 <= i < getPerson(advertiserId).producers.length;getPerson(advertiserId).producers[i].equals(getPerson(addVertiserId)));
@ ensures (\forall int i; 0 <= i && i < \old(getPerson(advertiserId).producers.length;
@ \exists int j;0 <= j < getPerson(producerId).producers.length;
@ \old(getPerson(advertiserId).producers[i]).euqals(getPerson(advertiserId).producers[k]));
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !(\exists int i; 0 <= i && i < people.length;
@ people[i].equals(getPerson(producerId)));
@ signals (PersonIdNotFoundException e) (\exists int i; 0 <= i && i < people.length;people[i].equals(getPerson(producerId)))
@ && !(\exists int i; 0 <= i && i < people.length; people[i].equals(getPerson(advertiserId)));
@*/
void addAdvertise(int producerId,int advertiserId);
// 指定顾客关注某个广告
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].euqals(getPerson(customerId)) && people[i] instanceof Customer);
@ requires (\exists int i; 0 <= i && i < people.length; people[i].equals(getPerson(AdvertiserId)) && people[i] instanceof Advertiser);
@ assignable getPerson(customerId).attentions;
@ ensures getPerson(customerId).attentions.length == \old(getPerson(customerId).attentions.length) + 1;
@ ensures (\exists int i;0 <= i < getPerson(customerId).attentions.length;getPerson(customerId).attentions[i].equals(getPerson(AdvertiserId)));
@ ensures (\forall int i; 0 <= i && i < \old(getPerson(customerId).attentions.length;
@ \exists int j;0 <= j < getPerson(customerId).attentions.length;
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !(\exists int i; 0 <= i && i < people.length;
@ people[i].equals(getPerson(customerId)));
@ signals (PersonIdNotFoundException e) (\exists int i; 0 <= i && i < people.length;people[i].equals(getPerson(customerId)))
@ && !(\exists int i; 0 <= i && i < people.length; people[i].equals(getPerson(AdvertiserId)));
@*/
void addAttention(int customerId,int AdvertiserId);
// 指定顾客进行购买
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < people.length; people[i].euqals(getPerson(customerId)) && people[i] instanceof Customer);
@ requires (\exists int i; 0 <= i && i < people.length; people[i].equals(getPerson(AdvertiserId)) && people[i] instanceof producerId);
@ requires (\exists int i; 0 <= i && i < getPerson(customerId).attentions.length; (\exists int j;0 <= j && j < getPerson(customerId).attentions.length;getPerson(customerId).attentions[j].equals(getPerson(producerId)));
@ assignable getPerson(customerId).money;
@ assignable getPerson(producerId).saleVolume;
@ ensures getPerson(customerId).money == \old(getPerson(customerId).attentions.length) - getPerson(producerId).getProce();
@ ensures (\exists int i;0 <= i < getPerson(customerId).attentions.length;getPerson(customerId).attentions[i].equals(getPerson(AdvertiserId)));
@ ensures getPerson(customerId).volume == \old(getPerson(customerId).volume) + 1;
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !(\exists int i; 0 <= i && i < people.length;
@ people[i].equals(getPerson(customerId)));
@ signals (PersonIdNotFoundException e) (\exists int i; 0 <= i && i < people.length;people[i].equals(getPerson(customerId)))
@ && !(\exists int i; 0 <= i && i < people.length; people[i].equals(getPerson(producerId)));
@*/
void purchase(int customerId,int producerId);
// 查询销售量
void getSaleVolume(int producerId);
// 查询销售路径
void getSalePath(int producerId)
学习体会
本单元体会最深的便是对于JML的理解。
JML采用与程序或者数学语言相似的方式对含义进行精准的确定和传播,进而避免了自然语言上的歧义问题。在本单元的实践中,设计端JML语言定义接口,实现端也即我们新建自定义类实现接口,确实让我深刻感受到了严谨的美丽。同时,本单元对查询和更新指令的平衡,对图论知识的应用等都让我体会到了与前几个单元的不一样的感觉。
与前几个单元尤其不同的是,本单元对于性能有着较高的要求,而事实上性能和面向对象的思想也是存在有一定的冲突,显然大量的函数调用等均会花费额外的时间开销,同时,为了更好的性能,这也要求我们必须选择性的牺牲一部分内存,也就是典型的以空间换时间,最简单的,便是对每次更新后,尽可能对接下来将会访问的数据进行预处理乃至直接存储,同时,对于同一个对象,如Person,可能需要多种容器进行存储,当然,容器的选择本身也是一个问题。不过总体而言,OO对于性能的要求并不太高,同时没有性能分的要求,性能仅仅局限在有限的数据结构和算法上,因此在保证清晰结构下确保一定的性能总体而言还是不算太难。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号