Word Representation 词表示
一、概念和意义
1.1. One-Hot
在自然语言处理中,我们该怎样从语料中提取信息?语料是string的形式,无法计算,所以我们必须要把语料用向量表示。
最先引入最基本的表示方法 One Hot,根据词在词汇表的位置来表示这个词。

1.2. 语言模型 Language Model
表示后怎么用呢?一个朴素的概念是,当我们知道了上文,就能预测下个词是什么。设我们要预测的词语是\(w_k\),它前面有\(k-1\)个词语,那么到了第\(k\)个词时为\(w_k\)的概率是:
那么如何求的下个词的概率 \(P(w_1,w_2,w_3,...,w_k)\) ?
最朴素的思想,把其中每一个子项的概率全部求解出来,每一项都有 \(P(w_k|w_{1}^{k-1})=\frac{P(w_{1}^{k})}{P(w_{1}^{n-1})}\approx \frac{Count(w_{1}^{k})}{Count(w_{1}^{k-1})}\) ,只要求出来每一项,就知道下个词为的概率 \(w_k\) 了,这就是统计语言模型。
但显然基于统计的语言模型复杂度非常高,遍历统计每种几率不现实,所以逐步发展出了N-gram模型、基于神经网络的模型……
二、N-gram 模型
2.1. 概念
在上一节中,计算每一项 \(Count(w_{1}^{k})\) 是唯一耗时。为了简化问题,我们做一个假设,每个词的出现概率,只和它前面的N个词语有关,这就是N-gram模型了。
根据N-gram,我们有
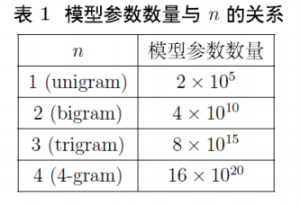
这样一来,需要统计的数量就变少了。那么 \(n\) 取多少呢?一般来说要考虑到模型复杂度和模型效果。复杂度方面,假定词汇有 \(|V|=2*10^5\) 个,由于整体复杂度是 \(O({N}^{n})\) ,因此一般不会取太大的 \(n\) 。实践中一般取 \(n=3\),称为 Three-Gram Model (三元模型)。
2.2. Smoothing 平滑化
问题背景
- 若n-gram公式中 \(Count(w_{k-n+1}^{k-1})=0\),能否认为 $ P(w_k|w_{1}^{k-1})=0$ ?
- 若n-gram公式中 \(Count(w_{k-n+1}^{k-1})=Count(w_{k-n+1}^{k})\),能否认为 $ P(w_k|w_{1}^{k-1})=1$ ?
- 留待思考
解决方案[3]
- Add-One Smoothing (Laplace Smoothing)
- 在现有语料基础上,假设每个可能的 N-gram 再发生一次。例如原来0次的现在就有1次共现,10次的就有11次共现。
- \( P(w_k|w_{1}^{k-1})= \frac{Count(w_{k-n+1}^{k})}{Count(w_{k-n+1}^{k-1})}→\frac{Count(w_{k-n+1}^{k})+1}{Count(w_{k-n+1}^{k-1})+V}\)
- \(V\) 表示词汇表 \(N-1\) 阶组合的数量,对bigram而言就是词汇表的大小。
- Add-One Smoothing 的缺点是对原先未共现的组合过于倾向。考虑到前面问题背景里给出的数据统计结论——“80%三元组不超过5次”,加1的操作对语料库中存在共现的组合产生了较大影响。因此在实际操作时可以不采用 \(V\) ,通过引入系数 \(\delta∈(0,1)\) ,使用 \(\delta V\) 来代替。
- Interpolation Smoothing (Jelinek-Mercer Smoothing) 差值平滑
- 以低阶元组的线性组合辅助表示高阶元组:
- \(P(w_k|w_{k-1},w_{k-2})=λ_1P(w_k|w_{k-1},w_{k-2})+λ_2P(w_k|w_{k-1})+λ_3P(w_k)\)
- 差值平滑中 \(P(w_k)\) 子项可以保证结果不为0。
- 参数 \(λ_i\) 可以通过最大似然估计的方式学习。但如果对所有元组单独学习 \(λ_i\) 会导致参数量过多,因此需要根据一定规则方式共享一部分 \(λ_i\) 参数,例如相同词性使用相同 \(λ_i\),或者全部词汇共享相同的 \(λ_i\)。
- Backoff Smoothing
- Good-Turing Smoothing
2.3. Perplexity 困惑度——评价语言模型的好坏[4]
在得到不同的语言模型(一元语言模型、二元语言模型....)的时候,我们如何判断一个语言模型是否好还是坏,一般有两种方法:
- 一种方法将其应用到具体的问题当中,比如机器翻译、speech recognition、spelling corrector等。然后看这个语言模型在这些任务中的表现(extrinsic evaluation,or in-vivo evaluation)。但是,这种方法一方面难以操作,另一方面可能非常耗时,可能跑一个evaluation需要大量时间,费时难操作。
- 针对第一种方法的缺点,大家想是否可以根据与语言模型自身的一些特性,来设计一种简单易行,而又行之有效的评测指标。于是,人们就发明了perplexity这个指标。
困惑度(perplexity)的基本思想是:给测试集的句子赋予较高概率值的语言模型较好,当语言模型训练完之后,测试集中的句子都是正常的句子,那么训练好的模型就是在测试集上的概率越高越好,公式如下:
由公式可知,句子概率越大,语言模型越好,迷惑度越小。
三、神经概率语言模型 NNLM
N-gram思路将计算的窗口范围缩减到了n个,但是仍然是一个统计概率语言模型,基于统计去进行概率估计。就像分类问题我们可以建模成神经网络模型,在语言模型中我们也可以引入神经网络的结构,通过训练每层之间的参数,拟合出语言概率的结果,这就是NNLM。
3.1. 概念
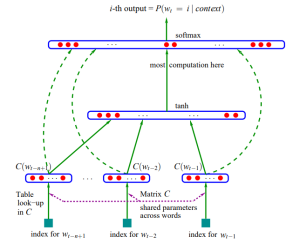
第一层是输入层,设每个词语是长度为 m 的 “distribution representation” 向量,一共有 n 个词,那么输入层shape 就是 (n, m)
第二层是投影层,把输入的每个词concat起来,输出shape = (1, nm)
第三层是隐藏层,是一个Dense(activation='tanh')的全连接,有参数 W 和 b 在这里训练,设隐藏层的输出是 h 维的(这里一般较小的数字就可以了,因为很影响计算量),那么输出shape = (nm, h)
第四层是输出层,是一个Dense(activation='tanh')的全连接softmax输出。有参数也在这一层训练。同时输出的向量大小是 (|V|, 1),|V|就是词汇表的大小。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号