03-Value-Based Reinforcement Learning

Value-Based Reinforcement Learning

一、Deep Q-Network (DQN)

本质就是用神经网络近似\(Q^*\)函数,将 \(Q^{*}(s_t,a_t)\) 当作是一个先知，先知可以告诉你每个动作带来的平均回报，我们就应该听先知的话选平均回报最高的动作

1. Goal:

   Win the game (≈ maximize the total reward.)

2. Question:

   If we know $ Q^{*}(s_t,a_t) $ , what is the best action?

3. Challenge:

   We do not know $ Q^{*}(s_t,a_t) $

   价值学习的基本想法就是选择一个函数来近似 $ Q^{*}(s_t,a_t) $

   比如超级玛丽玩个10w次，我们就基本上可以训练出一个先知了

   • Solution: Deep Q Network (DQN)

   • Use neural network \(𝑄(s,a;w)\) to approximate $ Q^{*}(s_t,a_t) $

     • w:神经网络的参数

     • s:状态s说神经网络的输入

     • 神经网络的输出是很多数值，也就是对各个可能的数值的打分，每一个动作a对应一个分数。我们通过奖励来学习这个神经网络，这个神经网络的打分会越来越准。当神经网络玩了几百万次游戏后，神经网络将和先知一般

1.1 Apply DQN to Play Game

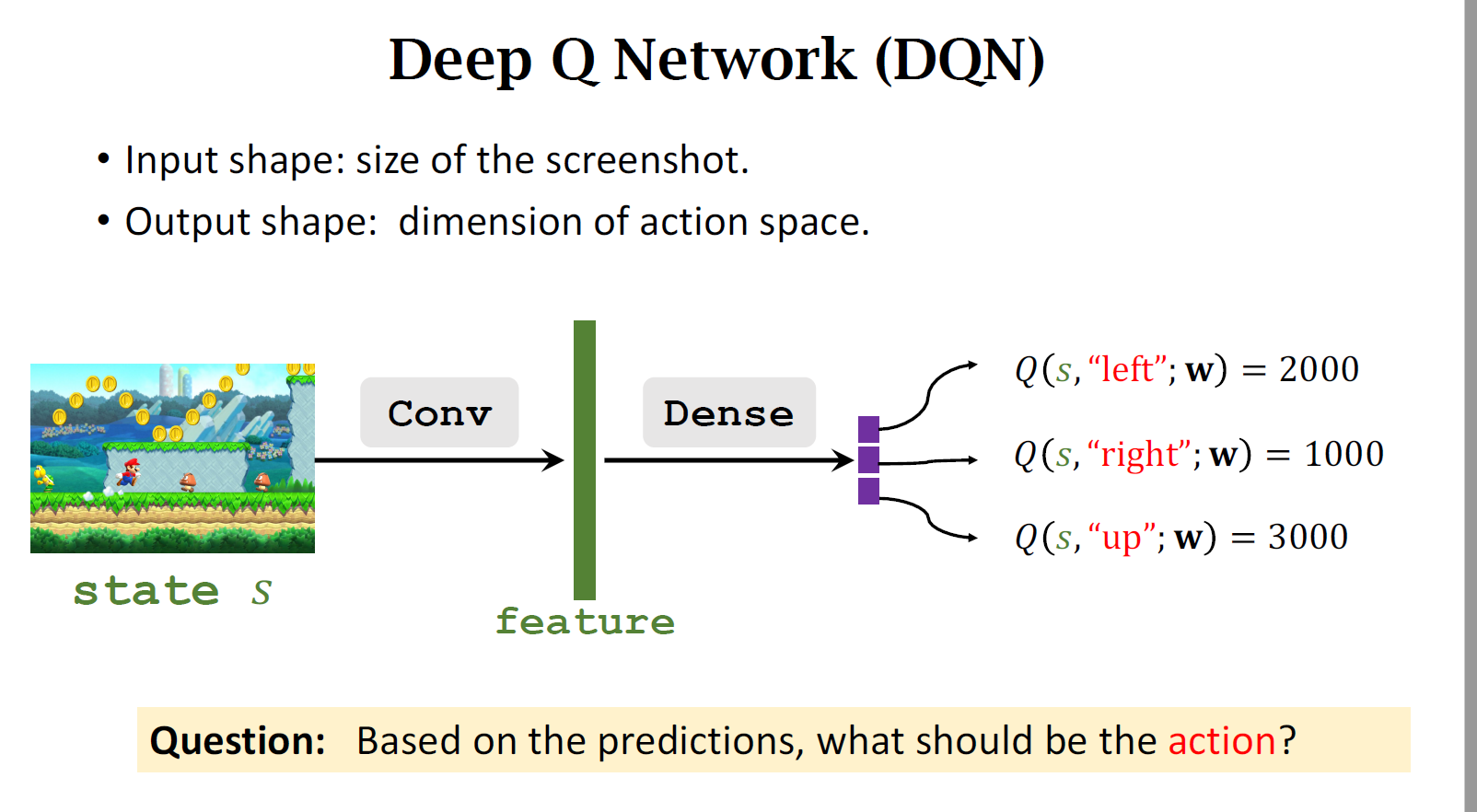
• 卷积层把图片变成特征向量，通过几个全链接层把特征映射到一个输出向量，输出向量也就是对动作打分，向量的每一个元素对应于一个动作，此情况有左右上三个动作所以是三维向量

• 所以只要把DQN训练好，就可以用DQN自动控制超级玛丽打赢游戏

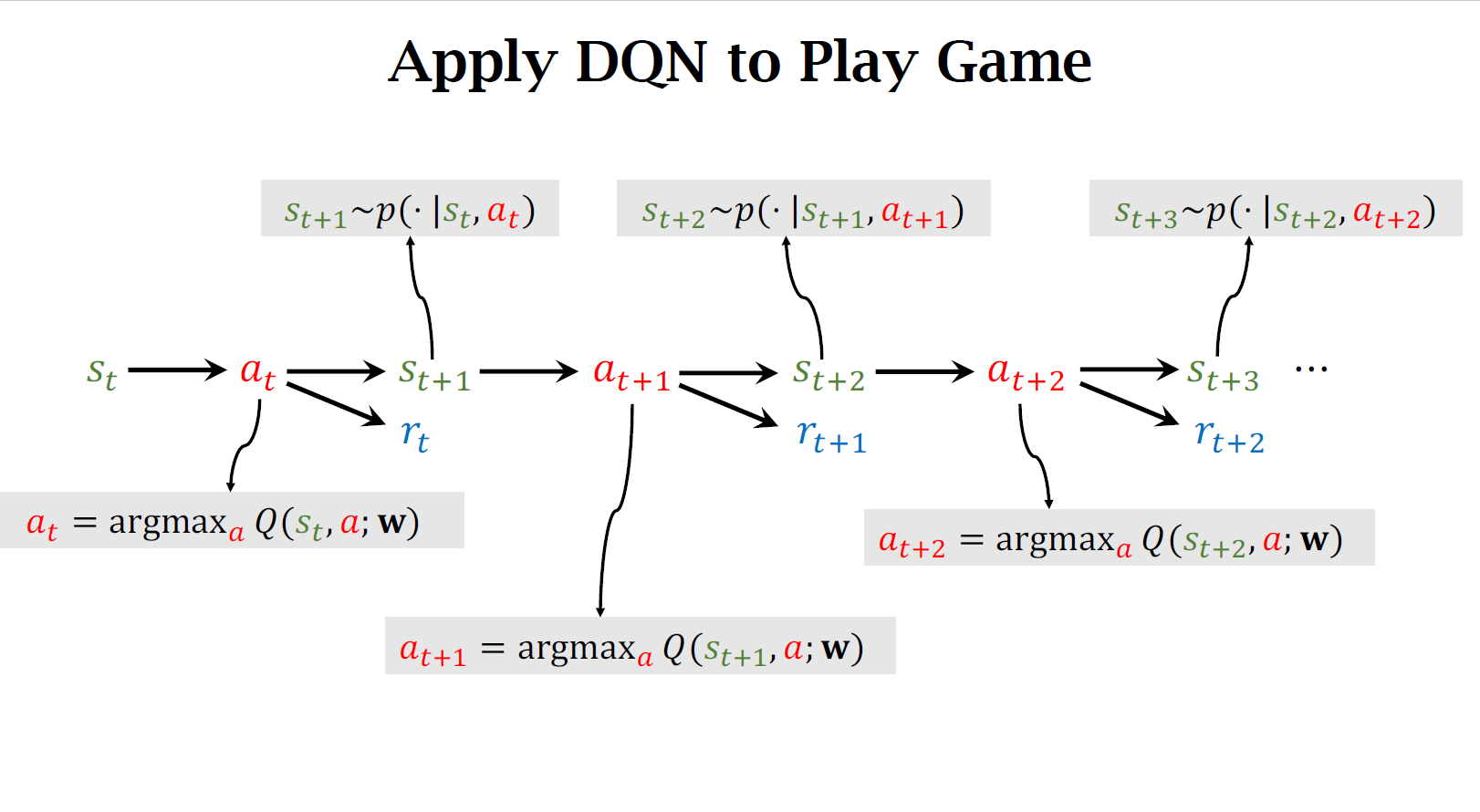
上图步骤：

1. 当前观测到状态\(s_t\)用DQN把状态\(s_t\)作为输入，给所有的动作打分，选出分数最高的动作，作为\(a_t\)

   

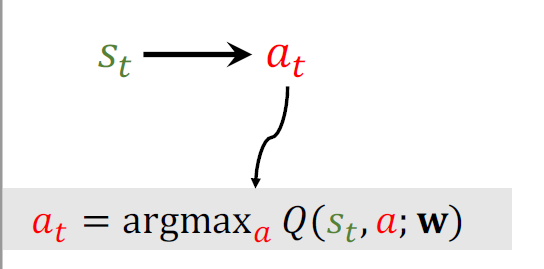
2. agent做出\(a_t\)这个动作后环境将会改变状态，用状态转移函数\(p\)来抽一个新的状态\(s_{t+1}\),环境将告诉我们这一步的奖励\(r_t\),奖励可以是+或-或0

   

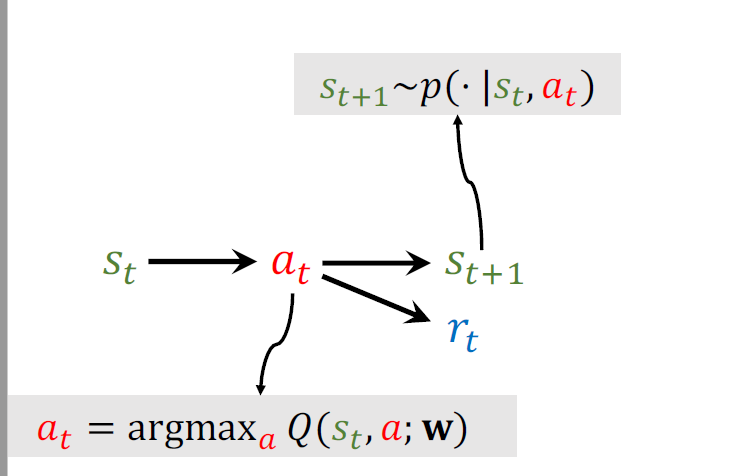
3. 有了新的状态\(s_{t+1}\),重复1和2，直到游戏结束

二、Temporal Difference (TD) Learning

2.1 Example

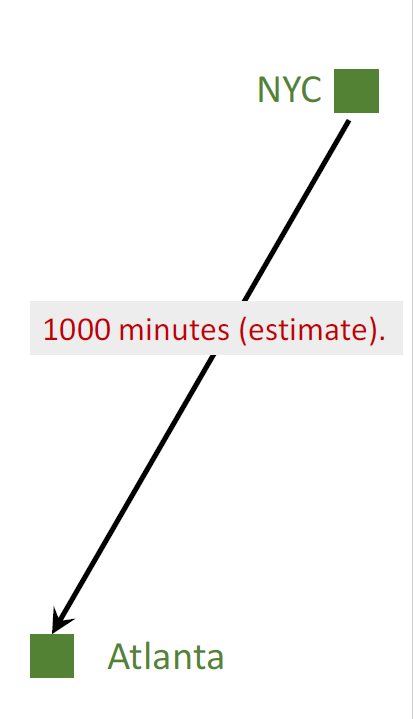
• I want to drive from NYC to Atlanta.

• Model \(Q(w)\) estimates the time cost, e.g., 1000 minutes.

模型 \(Q(w)\) 最开始并不准确，某种意义上可以说是纯随机的，但是随着更多人用这个模型得到更多数据，更多训练，这个模型就会越来越准，会像谷歌地图一样准确

• Question1: How do I update the model?

  

  我需要怎么样的数据，有了这些数据后我又该如何更新模型参数呢？

  • Make a prediction: \(𝑞 = Q(w)\) , e.g., 𝑞 = 1000

  • Finish the trip and get the target 𝑦, e.g., 𝑦 = 860.

  • Loss: \(L=\frac{1}{2} (q-y)^2\)

  • 
  • 

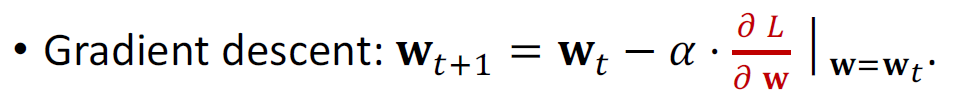
    使用梯度下降更新模型参数，因为梯度下降减小了loss使得预测值和真实值更接近了

• Can I update the model before finishing the trip?

  在结束一次旅行前可以更新模型吗？

• Can I get a better 𝐰 as soon as I arrived at DC?

  

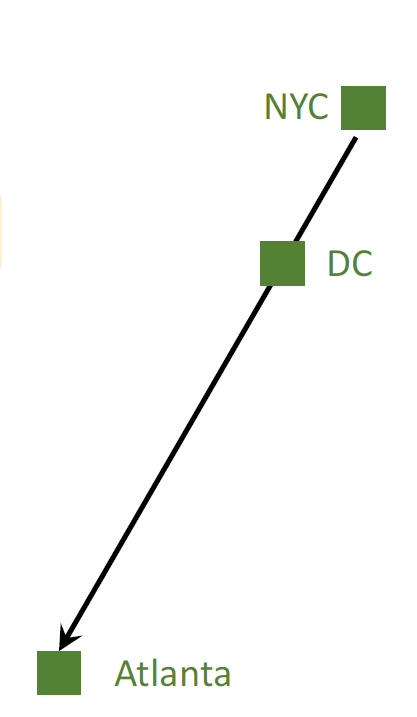
  能否使用纽约到亚特兰大这一部分来更新模型呢？

可以的，我们可以使用TD算法来做这一件事

• Model’s estimate:
  NYC to Atlanta: 1000 minutes (estimate).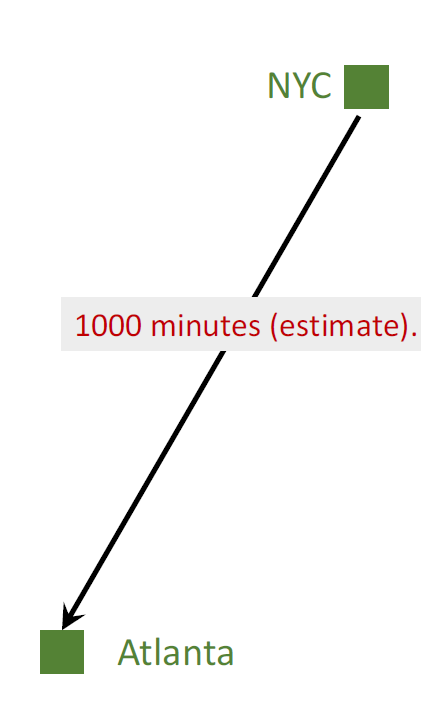

  

• I arrived at DC; actual time cost:
  NYC to DC: 300 minutes (actual).

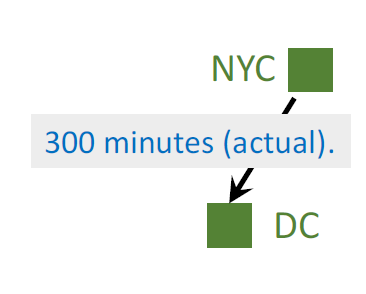
• Model now updates its estimate:
  DC to Atlanta: 600 minutes (estimate).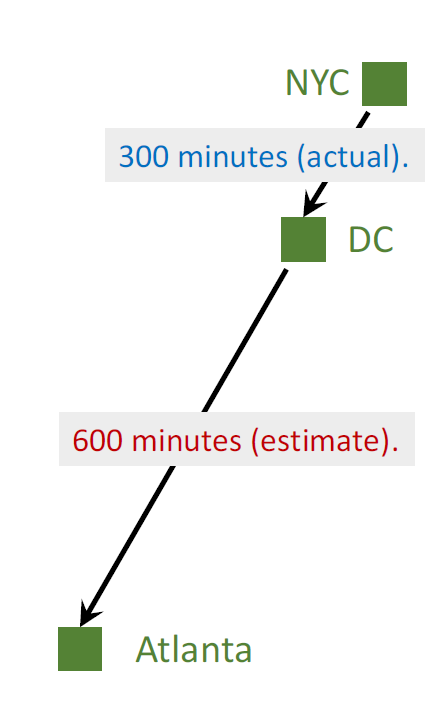

  

• Model’s estimate: \(Q(w)\) = 1000 minutes.

• Updated estimate: 300 + 600 = 900（TD target） minutes.

  我越接近亚特兰大，TD target也就越准，用TD target的话我不需要跑完全部过程来直到真实的开销，随时可以更新TD target

  

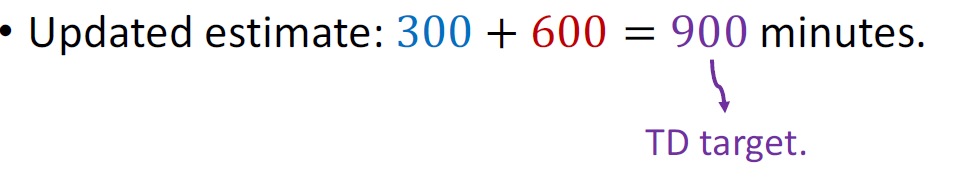
• TD target y = 900 is a more reliable estimate than 1000.

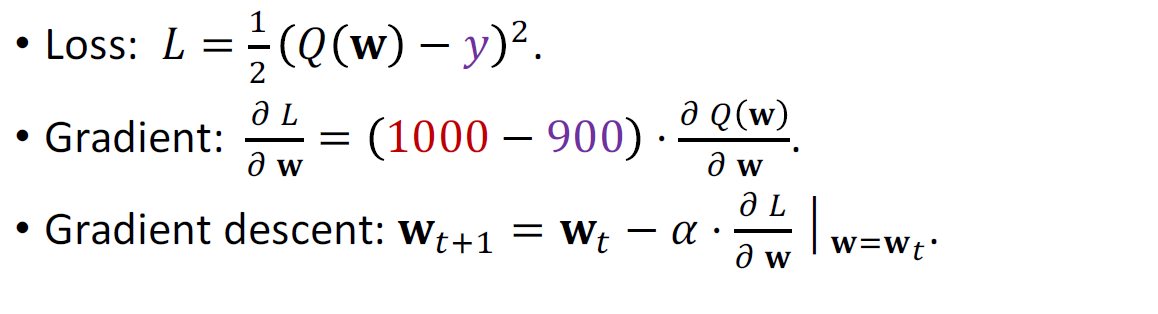
2.2 Why does TD learning work?

• Model’s estimates:
  • NYC to Atlanta: 1000 minutes.
  • DC to Atlanta: 600 minutes.
  • NYC to DC: 400 minutes.
• Ground truth:
  • NYC to DC: 300 minutes.
• TD error: \(𝛿 = 400 − 300 = 100\)

2.3 TD算法的目标

使得TD error尽可能接近0，也就是预计时间与实际时间相同，我们可以使用梯度下降来减少TD error

三、TD Learning for DQN

3.1 How to apply TD learning to DQN?

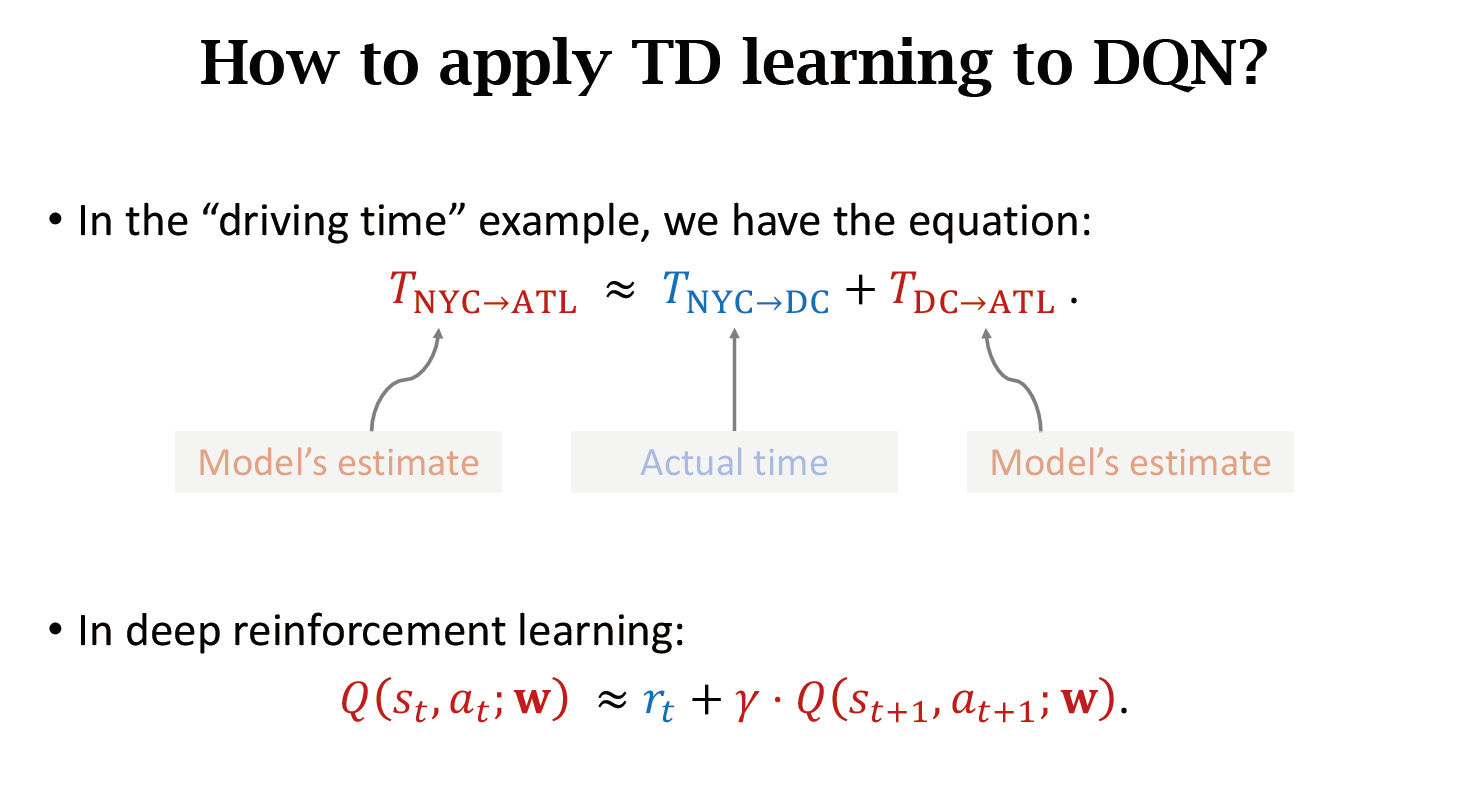
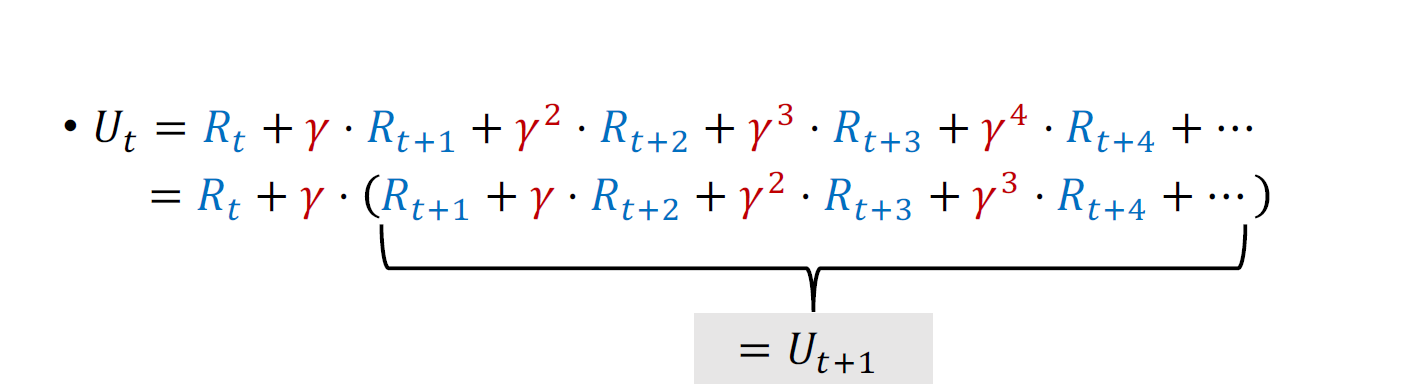
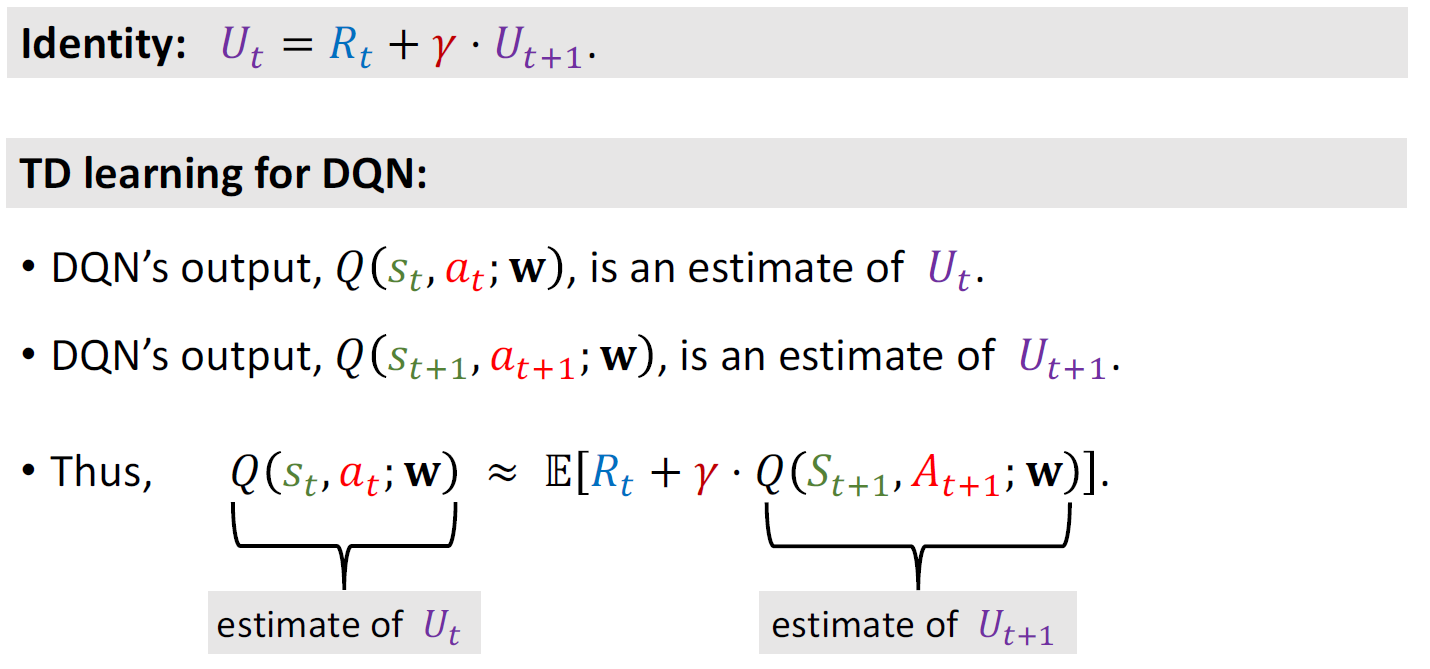
左边是对\(U_{t}\)的近似，右边是对\(U_{t+1}\)的近似，又因为：

所以左右大致相等

3.2 Train DQN using TD learning

四、Summary